Rの関数から gls {nlme} を確認します。
gls関数について
glsは、Generalized Least Squares(一般化最小二乗法)を用いて線形モデルをフィッティングするための関数です。
通常の線形モデル(lm()関数で実行されるもの)は、誤差項が互いに独立であり、かつ分散が均一である(等分散性)という仮定を置いています。
しかし、実際のデータ、特に時系列データや反復測定データなどでは、誤差項間に相関があったり(自己相関)、分散が一定でなかったり(不等分散性)することがあります。
このような場合に通常の最小二乗法を適用すると、回帰係数の推定値自体は不偏(偏りがない)ですが、その標準誤差を過小評価してしまい、結果として誤った統計的推論(例えば、有意でない変数を有意と判断するなど)を導く可能性があります。
gls関数は、モデルに誤差の相関構造や不等分散性を組み込むことを可能にします。
それゆえ、より現実に即したモデルを構築し、信頼性の高いパラメータ推定と統計的検定を行うことができます。
gls関数の引数
以下にgls関数の各引数について確認します。
model: モデルの構造を定義するformulaオブジェクトを指定します。応答変数と説明変数の関係を応答変数 ~ 説明変数1 + 説明変数2のように記述します。これはlm関数と同様の形式です。data: モデルで使用するデータが含まれたデータフレームを指定します。correlation: 誤差項の相関構造を指定します。nlmeパッケージが提供するcorStructクラスのオブジェクトを使用します。例えば、時点tとt-1の誤差に相関がある一次自己回帰モデル(AR(1))を仮定する場合はcorAR1()を、時点によらず全ての観測間の相関が等しい複合対称性を仮定する場合はcorCompSymm()を指定します。デフォルトはNULLで、この場合、誤差は独立であると仮定されます。weights: 誤差項の不等分散性をモデル化するために使用します。varFuncクラスのオブジェクトを指定します。例えば、誤差の分散が特定の説明変数のべき乗に比例すると仮定する場合にはvarPower()を、複数のグループで分散が異なると仮定する場合にはvarIdent()を使用します。デフォルトはNULLで、この場合、誤差は等分散であると仮定されます。subset:data引数で指定したデータフレームの一部を使用してモデルをフィッティングする場合に、そのサブセットを定義する論理式やインデックスベクトルを指定します。method: パラメータの推定方法を指定します。“REML”(Restricted Maximum Likelihood: 制限付き最尤法)または “ML”(Maximum Likelihood: 最尤法)から選択します。固定効果の推定値は両者で同じですが、分散コンポーネントの推定値が異なります。デフォルトは"REML"です。na.action: データに欠損値(NA)が含まれる場合の処理方法を指定する関数です。デフォルトはna.failで、欠損値があるとエラーを返します。na.omit(欠損値のある行を削除)やna.excludeなども選択できます。control: モデルのフィッティングアルゴリズムを制御するためのパラメータをリスト形式で指定します。glsControl()関数で詳細な設定が可能です。例えば、最適化の最大反復回数(maxIter)や収束判定の許容誤差(tolerance)などを設定できます。verbose: 論理値(TRUEまたはFALSE)を指定します。TRUEに設定すると、最適化の過程がコンソールに出力されます。モデルが収束しない場合などに、問題の診断に利用します。
シミュレーション
それでは、gls関数を確認するためのシミュレーションを行います。ここでは2つのシナリオ、「不等分散性」と「自己相関」を持つデータを生成します。
なお、有意水準は5%とします。
シナリオ1: 誤差に不等分散性が存在する場合
# 必要なパッケージを読み込みます
library(nlme)
library(ggplot2)
# シミュレーション結果の再現性を担保するために乱数シードを設定します
seed <- 20251018
set.seed(seed)
# --- データの生成 ---
# 説明変数xが増加するにつれて、誤差のばらつき(分散)が大きくなるデータを生成します
n <- 100
x1 <- runif(n, 5, 100)
# 誤差の標準偏差がx1の0.8乗に比例するように設定します
error1 <- rnorm(n, mean = 0, sd = x1^0.8)
# 真のモデルは y = 10 + 2*x です
y1 <- 10 + 2 * x1 + error1
data1 <- data.frame(x1, y1)
# 散布図の描画
p1 <- ggplot(data1, aes(x = x1, y = y1)) +
geom_point(alpha = 0.6, color = "blue") +
labs(
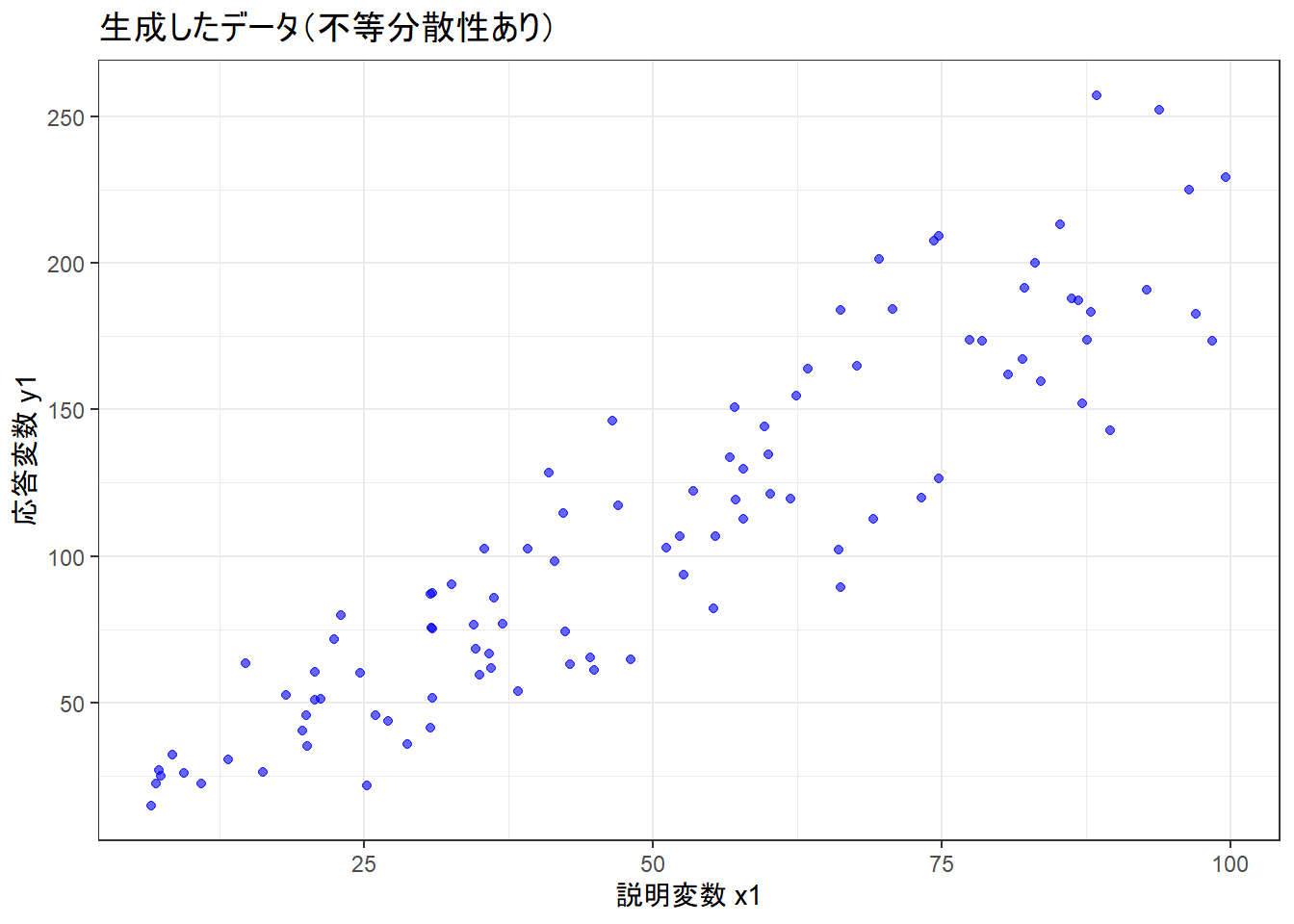
title = "生成したデータ(不等分散性あり)",
x = "説明変数 x1",
y = "応答変数 y1"
) +
theme_bw()
print(p1)x1が大きくなるほど、y1のばらつきが大きくなっていることが確認できます。
通常の線形モデル(lm)による分析
# このモデルは誤差の等分散性を仮定しています
lm_fit <- lm(y1 ~ x1, data = data1)
print(summary(lm_fit))
# 残差プロット
plot_data_lm <- data.frame(
fitted = fitted(lm_fit),
resid = rstandard(lm_fit)
)
p2 <- ggplot(plot_data_lm, aes(x = fitted, y = resid)) +
geom_point(alpha = 0.6, color = "red") +
geom_hline(yintercept = 0, linetype = "dashed") +
labs(
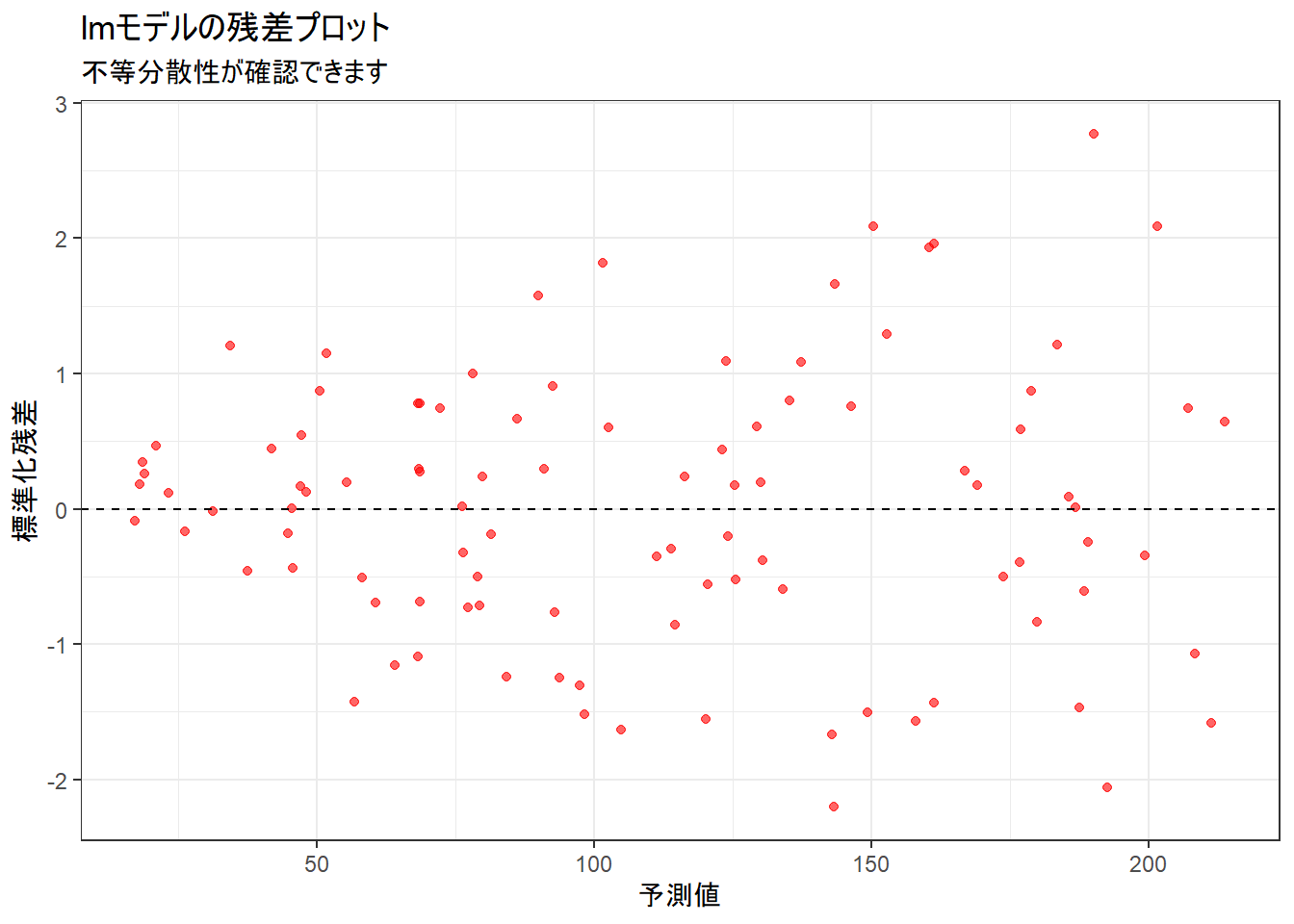
title = "lmモデルの残差プロット",
subtitle = "不等分散性が確認できます",
x = "予測値",
y = "標準化残差"
) +
theme_bw()
print(p2)
Call:
lm(formula = y1 ~ x1, data = data1)
Residuals:
Min 1Q Median 3Q Max
-53.898 -15.268 1.362 15.726 67.097
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.15338 5.34880 0.59 0.557
x1 2.11490 0.09435 22.42 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 24.62 on 98 degrees of freedom
Multiple R-squared: 0.8368, Adjusted R-squared: 0.8351
F-statistic: 502.5 on 1 and 98 DF, p-value: < 2.2e-16残差のばらつきが予測値の増加に伴って広がっており、「不等分散性」が確認できます。
このような場合、lmによる標準誤差の推定は信頼できません。
glsによる不等分散性のモデル化
weights引数にvarPower()を指定し、分散がx1のべき乗に比例することをモデルに組み込みます。
# weights = varPower(form = ~x1)は、Var(error) = (sigma * |x1|^delta)^2 という分散構造を仮定します
gls_fit_var <- gls(y1 ~ x1, data = data1, weights = varPower(form = ~x1))
print(summary(gls_fit_var))Generalized least squares fit by REML
Model: y1 ~ x1
Data: data1
AIC BIC logLik
908.3388 918.6787 -450.1694
Variance function:
Structure: Power of variance covariate
Formula: ~x1
Parameter estimates:
power
0.6152235
Coefficients:
Value Std.Error t-value p-value
(Intercept) 6.928272 2.7975266 2.47657 0.015
x1 2.036601 0.0781075 26.07433 0.000
Correlation:
(Intr)
x1 -0.772
Standardized residuals:
Min Q1 Med Q3 Max
-2.26446935 -0.82661710 0.01814318 0.69765749 2.30362503
Residual standard error: 2.21049
Degrees of freedom: 100 total; 98 residuallmとglsのモデル結果比較
2つのモデルの出力結果は、誤差の分散構造をどのように扱うかによって、統計的推論が大きく変わりうることを示しています。
回帰係数の推定値と統計的有意性
はじめに、回帰係数 (Coefficients) の推定結果を比較します。
-
lmモデル (通常の線形モデル)- 切片 (Intercept): 3.15338 (p値 = 0.557)
- 傾き (x1): 2.11490 (p値 < 2e-16)
-
glsモデル (不等分散性を考慮したモデル)- 切片 (Intercept): 6.928272 (p値 = 0.015)
- 傾き (x1): 2.036601 (p値 = 0.000)
傾き(x1)の推定値は両モデルで近い値 (2.11 と 2.04) を示しており、いずれも統計的に有意です。
しかし、切片(Intercept)の評価が異なります。lmモデルではp値が0.557であり、統計的に有意ではありませんでした。この結果だけを見ると、「切片は0と異なるとは言えない」と結論づけてしまいます。一方で、不等分散性をモデルに組み込んだglsモデルでは、切片の推定値が6.928へと変わり、p値が0.015と5%水準で統計的に有意であるという結論に変わります。
標準誤差 (Std. Error) の違い
上記の統計的評価の違いは、パラメータの標準誤差が異なることに起因します。
-
lmモデル:- 切片の標準誤差: 5.34880
- 傾きの標準誤差: 0.09435
-
glsモデル:- 切片の標準誤差: 2.797527
- 傾きの標準誤差: 0.078108
glsモデルの方が、特に切片において標準誤差が小さくなっていることが確認できます。
lmは、データ全体のばらつきを均一なものとして平均化してしまうため、本来よりも不確実性が大きい(標準誤差が大きい)推定を行ってしまいます。
対照的にglsは、説明変数x1が小さい領域のデータ(ばらつきが小さい)をより重視して切片を推定するため、より精度良く(標準誤差が小さく)推定できています。
誤差分散のモデル化
この違いが生まれる最大の理由は、glsモデルの出力に含まれるVariance functionのセクションにあります。
Variance function:
Structure: Power of variance covariate
Formula: ~x1
Parameter estimates:
power
0.6152235 この出力は、glsが「誤差の分散はx1の値に依存して変化する」という構造をモデルに組み込んでいることを示しています。
具体的には、分散がx1のべき乗(power = 0.615)に従って大きくなることをデータから学習しています。
lmモデルにはこのような機能はなく、全ての誤差が単一の分散(Residual standard error: 24.62の2乗)に従うと仮定しています。
シミュレーションの残差プロット( Figure 2 )で確認した通り、この仮定は明らかにデータと矛盾していました。
結論
以上の比較から、誤差に不等分散性が存在する場合、その構造を無視した通常の線形モデル(lm)では、パラメータの標準誤差を不適切に推定してしまい、誤った統計的結論(今回の例では、本来有意であるはずの切片を有意でないと判断する)を導く危険性があることが確認できました。
glsは、weights引数を用いて不等分散性をモデル化することで、観測値ごとに異なるばらつきを考慮した、より信頼性の高いパラメータ推定と統計的検定を可能にします。
それゆえ、データの構造を正しく診断し、適切なモデルを選択することの重要性が、両者の比較から浮き彫りになります。
シナリオ2: 誤差に自己相関が存在する場合
# --- データの生成 ---
# 時間(time)の経過に伴い、ある時点の誤差が前の時点の誤差の影響を受けるデータを生成します
time <- 1:n
# 1次の自己回帰過程(AR(1))に従う誤差を生成します。phi=0.7は自己相関の強さを示します
error2 <- arima.sim(model = list(ar = 0.7), n = n, sd = 5)
# 真のモデルは y = 5 + 0.8*time です
y2 <- 5 + 0.8 * time + error2
data2 <- data.frame(time, y2)
p3 <- ggplot(data2, aes(x = time, y = y2)) +
geom_line(color = "darkgreen") +
geom_point(alpha = 0.6, color = "darkgreen") +
labs(
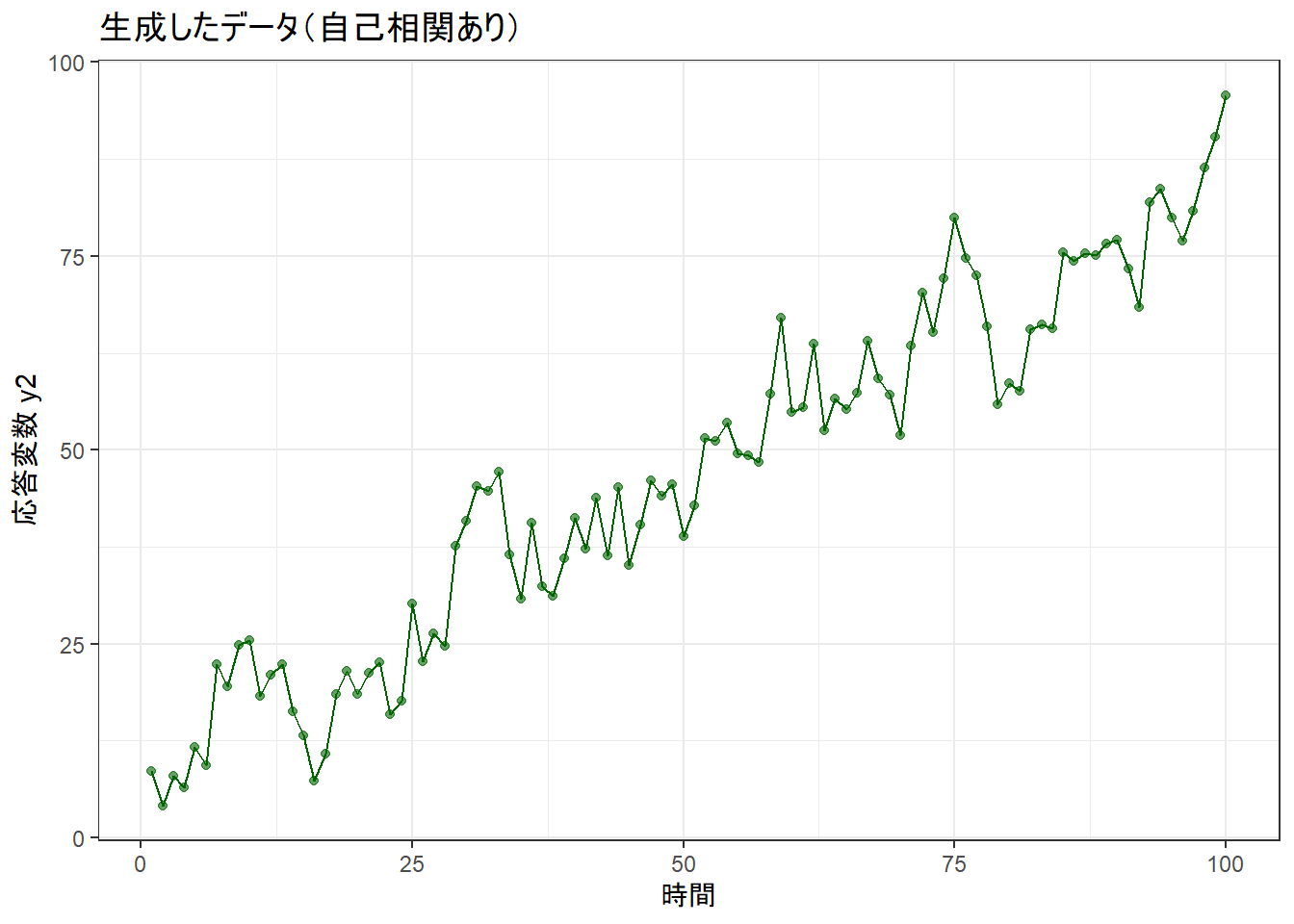
title = "生成したデータ(自己相関あり)",
x = "時間",
y = "応答変数 y2"
) +
theme_bw()
print(p3)通常の線形モデル(lm)による分析
lm_fit2 <- lm(y2 ~ time, data = data2)
print(summary(lm_fit2))
# ACFプロット
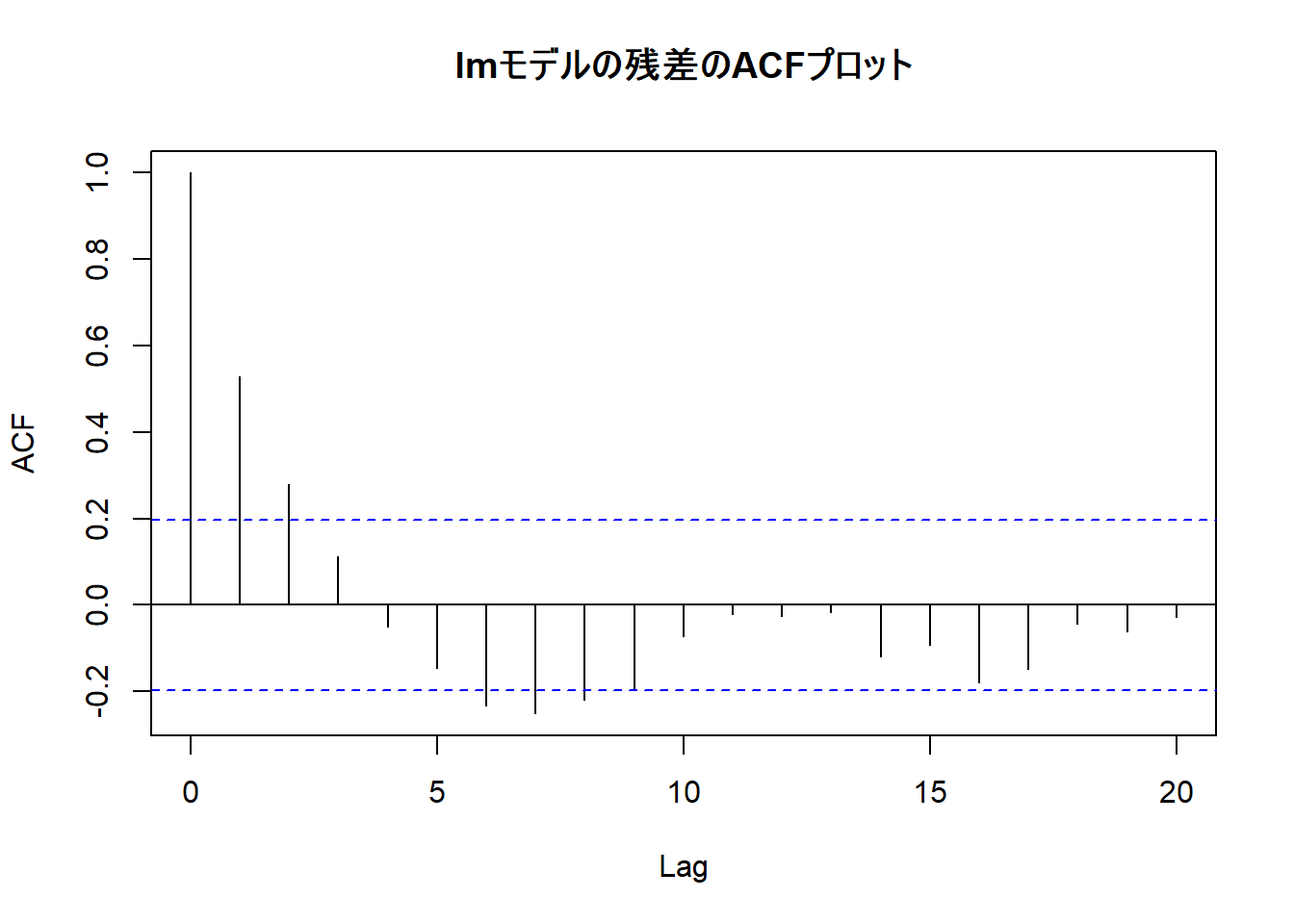
acf(residuals(lm_fit2), main = "lmモデルの残差のACFプロット")
Call:
lm(formula = y2 ~ time, data = data2)
Residuals:
Min 1Q Median 3Q Max
-12.8389 -4.0973 -0.5222 3.6840 14.4143
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.95400 1.25117 6.357 6.53e-09 ***
time 0.76724 0.02151 35.669 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 6.209 on 98 degrees of freedom
Multiple R-squared: 0.9285, Adjusted R-squared: 0.9278
F-statistic: 1272 on 1 and 98 DF, p-value: < 2.2e-16このACFプロット( Figure 4 )からは、以下の点が確認できます。
自己相関の存在: ラグ1、2の自己相関が、青い点線の有意水準の閾値を超えています。特にラグ1では自己相関係数が0.5を上回っており、ある時点の誤差が、その直前の時点の誤差と強い正の相関を持っていることがわかります。
lmモデルの仮定違反: 通常の線形モデルは、誤差項が互いに独立である(自己相関がない)ことを前提としています。Figure 4 は、その前提が満たされていないことを示しています。モデルの残差に、予測可能なパターン(時間的構造)が残ってしまっている状態です。
glsによる自己相関のモデル化
correlation引数にcorAR1()を指定し、誤差がAR(1)過程に従うことをモデルに組み込みます。
# form = ~time は、時間変数timeに基づいて相関を計算することを意味します
gls_fit_cor <- gls(y2 ~ time, data = data2, correlation = corAR1(form = ~time))
print(summary(gls_fit_cor))Generalized least squares fit by REML
Model: y2 ~ time
Data: data2
AIC BIC logLik
623.737 634.0769 -307.8685
Correlation Structure: AR(1)
Formula: ~time
Parameter estimate(s):
Phi
0.5739206
Coefficients:
Value Std.Error t-value p-value
(Intercept) 7.658532 2.3967922 3.195326 0.0019
time 0.775923 0.0409307 18.957022 0.0000
Correlation:
(Intr)
time -0.862
Standardized residuals:
Min Q1 Med Q3 Max
-2.0475296 -0.6533291 -0.1209754 0.5549909 2.1975143
Residual standard error: 6.39734
Degrees of freedom: 100 total; 98 residuallmとglsのモデル結果比較
提示された2つのモデル出力は、時系列データなどで見られる「誤差の自己相関」を無視することが、統計的推論にいかに影響を与えるかを示しています。
誤差構造のモデル化
両モデルの根本的な違いは、誤差の相関構造の扱いにあります。
lmモデル (通常の線形モデル)誤差項が互いに独立であることを前提としています。ACFプロット( Figure 4 )で確認した通り、このデータではその前提が満たされていませんでした。
glsモデル (自己相関を考慮したモデル)出力内の
Correlation Structureセクションが、このモデルの核心部分です。Correlation Structure: AR(1) Formula: ~time Parameter estimate(s): Phi 0.5739206上記の出力は、
glsが誤差間に1次の自己回帰 (AR(1)) 構造を仮定し、その自己相関係数 (Phi) をデータから0.574と推定したことを示しています。これは、ある時点の誤差が、1つ前の時点の誤差の約57%を引き継いでいることを意味します。
この推定により、データが持つ時間的な依存構造をモデルに正しく組み込んでいます。
回帰係数の推定値と標準誤差
次に、回帰係数(Coefficients)の推定結果を比較します。
-
lmモデル:- 切片 (Intercept): 7.95400 (標準誤差: 1.25117)
- 傾き (time): 0.76724 (標準誤差: 0.02151)
-
glsモデル:- 切片 (Intercept): 7.658532 (標準誤差: 2.396792)
- 傾き (time): 0.775923 (標準誤差: 0.040931)
回帰係数の推定値そのもの(切片や傾き)は、両モデルで比較的近い値になっています。しかし、その推定の信頼性を示す標準誤差 (Std.Error) が異なっています。
この差が生じる理由は、lmモデルが誤差の独立性を仮定することにより、データが持つ情報の量を過大評価してしまうためです。
正の自己相関があるデータでは、隣り合うデータ点が似たような値を取りやすいため、独立なデータ100点分よりも実質的な情報量は少なくなります。
lmはこの事実を無視するため、パラメータを過剰な精度で推定しているように見せかけ、結果として標準誤差を不当に小さく計算してしまいます。
一方、glsは自己相関の構造をモデル化することで、この「見かけ上の情報量」を適切に割り引き、より現実的で大きな標準誤差を算出します。
統計的推論への影響
標準誤差の違いは、t値 (t-value) に直接影響します。
t値は「係数の推定値 / 標準誤差」で計算されるため、標準誤差が小さいlmモデルではt値が非常に大きくなっています(例: timeのt値は35.7)。
今回のシミュレーションでは、timeの効果が強かったため、どちらのモデルでも統計的に有意であるという結論に変わりはありませんでした。
しかし、もし効果の有無が微妙なケース(例えば、p値が0.05近辺になるような場合)であれば、lmモデルは係数の効果を過大評価し、「本来は有意でない効果を、誤って有意である」と結論づけてしまう第一種の過誤を犯すリスクが非常に高くなります。
結論
時系列データのように誤差間に自己相関が疑われる状況で、その構造を無視したlmを用いると、パラメータの標準誤差を過小評価し、結果として係数の統計的有意性を過大に評価してしまう危険性があります。
glsは、correlation引数を用いて誤差の相関構造をモデルに組み込むことで、より正確な標準誤差を推定し、信頼性の高い統計的推論を可能にします。
それゆえ、データの背後にある構造を正しく捉え、適切なモデルを適用することの重要性が、両者の結果の比較から確認できます。
以上です。