Rの関数から pp.test {tseries} を確認します。
本ポストはこちらの続きです。

pp.test関数について
pp.testは、フィリップス–ペロン検定(Phillips-Perron Test) を実行するための関数です。この検定も、拡張ディッキー–フラー(ADF)検定と同様に、時系列データに単位根が存在するかどうかを判断するための単位根検定の一種です。
ADF検定との違い
pp.testとADF検定は、帰無仮説(「単位根が存在する」)と対立仮説(「定常である」)が同じであり、同じ目的で使用されますが、検定の内部的なアプローチに違いがあります。
- ADF検定: 時系列の誤差項に自己相関がある場合、その影響を排除するために、回帰モデルにラグ付けされた差分項を追加(モデルを拡張)します。このアプローチはパラメトリックな修正と言えます。
- PP検定: ADF検定のようにラグ項を追加しません。代わりに、より単純な回帰モデルを使い、その後に検定統計量自体を非パラメトリックな方法で修正することで、誤差項の自己相関の問題に対処します。
検定のp値が、あらかじめ設定した有意水準(例えば0.05)よりも小さい場合、帰無仮説は棄却され、「データは定常である」と結論付けられます。
pp.test関数の引数について
library(tseries)
args(pp.test)function (x, alternative = c("stationary", "explosive"), type = c("Z(alpha)",
"Z(t_alpha)"), lshort = TRUE)
NULLx
検定の対象となる数値ベクトル、または時系列オブジェクトを指定します。
alternative
対立仮説の種類を指定します。adf.testの引数と同様の役割を持ちます。
-
"stationary"(デフォルト): 対立仮説を「時系列は定常である」と設定します。p値が設定した有意水準より小さい場合に、データは定常であると判断されます。 -
"explosive": 対立仮説を「時系列は発散過程である」と設定します。
type
計算し、出力する検定統計量の種類を指定します。
-
"Z(alpha)": 正規化された係数に基づく検定統計量(Zα統計量)を使用します。 -
"Z(t_alpha)"(デフォルト): t統計量に基づく検定統計量(Zt統計量)を使用します。
lshort
検定統計量を修正する際に使用するラグの切り捨てパラメータ(truncation lag parameter)の計算方法を制御する論理値です。
-
TRUE(デフォルト): “short”バージョンとして、trunc(4*(length(x)/100)^0.25)という計算式でラグを決定します。 -
FALSE: “long”バージョンとして、trunc(12*(length(x)/100)^0.25)という計算式でラグを決定します。
このパラメータは、誤差項の自己相関をどの程度まで考慮して検定統計量を補正するかを調整します。
シミュレーション
pp.test関数の挙動を確認するために、「非定常なデータ」と「定常なデータ」を作成し、それぞれにpp.testを適用して結果を比較します。ADF検定と同様の結果が得られるはずです。
なお、有意水準は5%とします。
シミュレーションのためのサンプルデータ作成
# 再現性を確保するために乱数のシードを設定します
seed <- 20251011
set.seed(seed)
# データポイントの数を定義します
n <- 250
# 1. 非定常な時系列データ(ランダムウォーク)を作成します
# 単位根を持つ時系列の代表例です
# 非定常データの生成(単位根過程)
non_stationary_data <- cumsum(rnorm(n))
# 2. 定常な時系列データ(AR(1)過程)を作成します
# 自己回帰係数|φ|<1のAR(1)モデルは、定常過程の代表例です
# 定常データの生成(自己回帰過程)
stationary_data <- arima.sim(model = list(ar = 0.6), n = n)
# 描画デバイスの設定
# 1つのウィンドウに縦に2つのプロットを並べます
par(mfrow = c(2, 1), mar = c(4, 4, 3, 2))
# 非定常データをプロットします
plot(non_stationary_data,
type = "l", col = "darkblue",
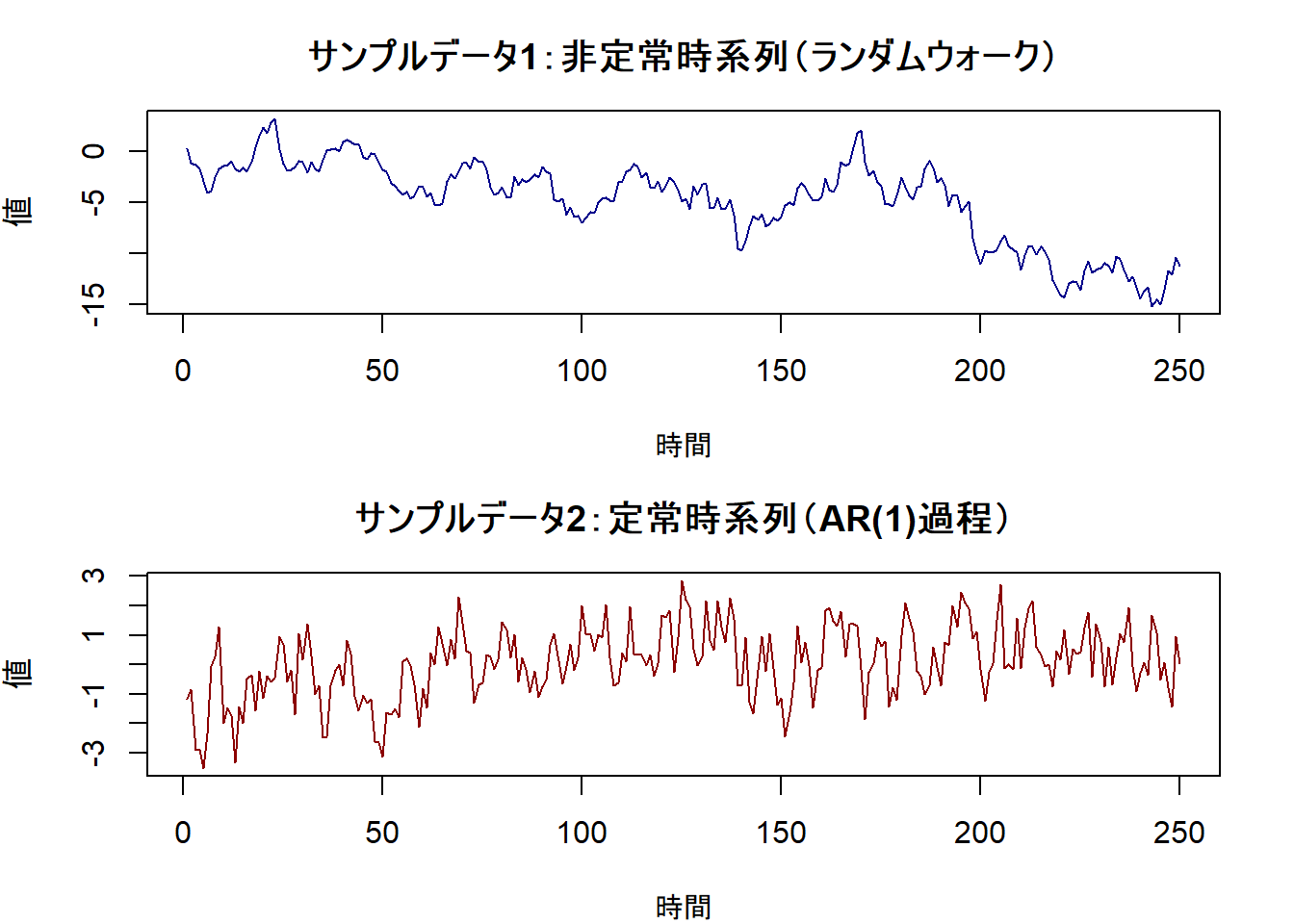
main = "サンプルデータ1:非定常時系列(ランダムウォーク)",
xlab = "時間", ylab = "値"
)
# 定常データをプロットします
plot(stationary_data,
type = "l", col = "darkred",
main = "サンプルデータ2:定常時系列(AR(1)過程)",
xlab = "時間", ylab = "値"
)ケース1:非定常データに対する検定
pp.testの帰無仮説は「単位根が存在する(非定常である)」です。非定常データですので、p値は有意水準5%より大きくなり、帰無仮説は棄却されないと予測されます。
pp_result1 <- pp.test(non_stationary_data)
print(pp_result1)
Phillips-Perron Unit Root Test
data: non_stationary_data
Dickey-Fuller Z(alpha) = -20.997, Truncation lag parameter = 5, p-value = 0.05453
alternative hypothesis: stationary pp.test検定結果の確認
この出力は、非定常な単位根過程(ランダムウォーク)として生成されたnon_stationary_dataに対して、フィリップス–ペロン(PP)検定を実行した結果です。
Phillips-Perron Unit Root Test
data: non_stationary_data
Dickey-Fuller Z(alpha) = -20.997, Truncation lag parameter = 5, p-value = 0.05453
alternative hypothesis: stationary各項目の確認
Phillips-Perron Unit Root Test実行された検定がフィリップス–ペロン単位根検定であることを示しています。
data: non_stationary_data検定に使用されたデータが
non_stationary_dataという名前のオブジェクトであることを示しています。Dickey-Fuller Z(alpha) = -20.997こちらがPP検定の検定統計量です。
Z(alpha)と表示されているのは、type引数のデフォルトが"Z(alpha)"であるためです。PP検定はディッキー–フラー検定のフレームワークを基礎としているため、このような名称が用いられます。この値は、内部的に計算された回帰係数を非パラメトリックな手法で修正したものです。Truncation lag parameter = 5ラグの切り捨てパラメータが
5に設定されたことを示しています。PP検定では、検定統計量を計算する過程で生じる誤差項の自己相関を修正するために、このパラメータを使用します。lshort = TRUE(デフォルト)の設定に基づき、データの長さ(250)から自動的に計算された値です。p-value = 0.05453p値は、この検定結果から結論を導くための指標です。p値は、「もし帰無仮説(データは単位根を持つ)が真実である場合に、観測された検定統計量と同等か、それ以上に極端な値が得られる確率」を示します。
alternative hypothesis: stationary対立仮説が「定常である(stationary)」に設定されていることを示しています。これは
alternative引数のデフォルト設定です。p値が設定した有意水準より小さい場合、帰無仮説が棄却され、こちらの対立仮説が採択されます。
結論の導出
検定の判断は、「p値」と事前に決めた「有意水準5%」を比較して行います。
- 帰無仮説 (H₀): 単位根が存在する(データは非定常である)。
- 判断ルール:
p値 < 有意水準であれば、帰無仮説を棄却する。
今回の結果を見てみましょう。
- p値:
0.05453 - 設定した有意水準:
0.05
0.05453 > 0.05ですので、p値は有意水準よりも大きいです。
ですので、帰無仮説「単位根が存在する」を棄却することはできません。
この検定結果は、「この時系列データが非定常である」という仮説と矛盾しないことを示しています。今回のデータは実際に単位根を持つ非定常データとして生成したものですので、検定が正しく機能していることが確認できます。
ケース2:定常データに対する検定
こちらのデータは定常ですので、p値は設定した有意水準より小さくなり、帰無仮説が棄却され、対立仮説「定常である」が採択されると予測されます。
pp_result2 <- pp.test(stationary_data)
print(pp_result2)
Phillips-Perron Unit Root Test
data: stationary_data
Dickey-Fuller Z(alpha) = -116.3, Truncation lag parameter = 5, p-value = 0.01
alternative hypothesis: stationary pp.test検定結果の確認
この出力は、定常な自己回帰過程(AR(1)過程)として生成されたstationary_dataに対して、フィリップス–ペロン(PP)検定を実行した結果です。
Phillips-Perron Unit Root Test
data: stationary_data
Dickey-Fuller Z(alpha) = -116.3, Truncation lag parameter = 5, p-value = 0.01
alternative hypothesis: stationary各項目の確認
Phillips-Perron Unit Root Test実行された検定がフィリップス–ペロン単位根検定であることを示しています。
data: stationary_data検定に使用されたデータが
stationary_dataという名前のオブジェクトであることを示しています。Dickey-Fuller Z(alpha) = -116.3PP検定の検定統計量です。
Truncation lag parameter = 5ラグの切り捨てパラメータが
5に設定されたことを示しています。こちらはデータの長さ(250)に基づいて自動的に計算された値で、検定統計量の補正に使用されます。p-value = 0.01p値は、検定結果の結論を導くための指標です。
alternative hypothesis: stationary対立仮説が「定常である(stationary)」に設定されていることを示しています。
結論の導出
検定の判断は、「p値」と事前に決めた「有意水準5%」を比較して行います。
- 帰無仮説 (H₀): 単位根が存在する(データは非定常である)。
- 判断ルール:
p値 < 有意水準であれば、帰無仮説を棄却する。
今回の結果を見てみましょう。
- p値:
0.01 - 設定した有意水準:
0.05
0.01 < 0.05ですので、p値は有意水準よりも小さいため、帰無仮説「単位根が存在する」を棄却します。
この検定結果は、対立仮説である「データは定常である」ことを示唆しています。今回のデータは実際に定常過程として生成したものですので、検定が正しく機能していることが確認できます。
パラメトリックな修正と非パラメトリックな修正
基本的な単位根検定(単純ディッキー–フラー検定)の回帰モデルは、以下の通りです。
Δyₜ = γ * yₜ₋₁ + εₜ
この検定が正しく機能するためには、誤差項 εₜ が「自己相関を持たない(例 : 昨日の誤差が今日の誤差に影響しない)」という前提条件があります。
しかし、例えば実際の経済データなどでは、この誤差項が自己相関を持っている(例:εₜがεₜ₋₁に影響される)ことがあります。この問題があると、計算される検定統計量が不正確になり、単位根検定の結果を信頼できなくなります。
ADF検定とPP検定は、この「誤差項の自己相関」という問題を解決するためのアプローチが異なるのです。
ADF検定:「パラメトリックな修正」とは
パラメトリック(Parametric) とは、「母数(パラメータ)」、つまりモデルの係数を用いて表現するアプローチを指します。
ADF検定は、誤差項εₜが持つ自己相関の構造を、自己回帰モデル(ARモデル)であると仮定し、その構造を直接モデルに組み込んでしまいます。
具体的には、元のシンプルな回帰式に、Δyのラグ項(Δyₜ₋₁, Δyₜ₋₂, …)を追加します。
修正後のモデル(ADF検定のモデル): Δyₜ = γ*yₜ₋₁ + β₁*Δyₜ₋₁ + β₂*Δyₜ₋₂ + ... + uₜ
このアプローチが「パラメトリックな修正」と呼ばれる理由は以下の通りです。
- 明示的なモデル化: 誤差の自己相関を、
β₁,β₂, … というパラメータ(係数)を持つΔyのラグ項によって明示的にモデル化しています。 - 構造の仮定: 「誤差の自己相関はAR(p)過程という特定の構造に従う」と仮定しています。
- 目的: 十分な数のラグ項を追加することで、最終的な新しい誤差項
uₜが自己相関を持たないようにすることを目指します。
つまり、ADF検定は、問題(自己相関)の原因を特定のモデル(ARモデル)だと考え、そのモデルを回帰式の中に直接組み込む(パラメータを追加する)ことで問題を解決します。
PP検定:「非パラメトリックな修正」とは
非パラメトリック(Non-parametric) とは、特定のモデル構造やパラメータを仮定せず、データそのものの性質から推定するアプローチを指します。
PP検定は、ADF検定のように回帰モデル自体には手を加えません。元のシンプルな回帰式をそのまま使います。
元のモデル(PP検定で使うモデル): Δyₜ = γ * yₜ₋₁ + εₜ
当然、このままでは誤差項 εₜ に自己相関が残っているため、ここから計算される検定統計量(例えばγのt値)は不正確です。
そこでPP検定は、計算が終わった後で、検定統計量そのものを直接修正します。
このアプローチが「非パラメトリックな修正」と呼ばれる理由は以下の通りです。
- モデルは変更しない: 回帰モデルにラグ項などを追加してパラメータを増やすことはしません。
- 事後的な修正: まずは不正確な検定統計量を計算しておき、その後に誤差項
εₜの性質(自己相関や分散)を直接データから推定します。 - 仮定が少ない: 誤差の自己相関が「AR(p)過程である」といった特定の構造を仮定しません。より一般的な自己相関の構造を許容します。そして、その自己相関の強さなどを用いて、検定統計量を補正するための「修正項」を計算し、元の統計量に加減算します。
つまり、 PP検定は、回帰モデルはシンプルなままにしておき、問題(自己相関)が検定統計量に与える悪影響の大きさをデータから直接見積もり、その影響分を統計量の値から差し引く(修正する)ことで問題を解決します。
まとめ
| 項目 | ADF検定 (パラメトリックな修正) | PP検定 (非パラメトリックな修正) |
|---|---|---|
| 基本思想 | モデルを修正して問題を解決する | 統計量を修正して問題を解決する |
| 修正の対象 | 回帰モデルの数式自体 | 計算された検定統計量の値 |
| 具体的な方法 | Δyのラグ項を説明変数として追加する | 誤差項の自己相関を推定し、統計量を補正する |
| 仮定 | 誤差の自己相関はAR(p)過程に従う | 誤差の自己相関について特定の構造を仮定しない |
以上です。