Rの関数から segmented {segmented}:一般化線形モデルの場合 を確認します。
segmented関数について
segmented関数は、構造変化点(ブレークポイント)が存在し、その点で回帰直線の傾きが変化するものの、変化点自体で回帰直線が不連続にジャンプしないような関係性を推定、モデル化することが出来る関数です。
本関数では、変化点の位置をモデルのパラメータとして直接推定することが可能です。
例えば、変化点のおおよその初期値を指定すると、関数は反復的なアルゴリズムを用いて、対数尤度を最大化する最適な変化点の位置を探索し、同時に各区間の回帰係数も推定します。
strucchangeパッケージのbreakpoints関数が、残差平方和を最小化する変化点の組み合わせを探索する(しばしば不連続なセグメントを許容する)のに対し、segmented関数は、連続性を仮定したモデルの枠組みの中で、変化点をパラメータとして推定する点にアプローチの違いがあります。
segmentedはジェネリック関数であり、lm(線形モデル)やglm(一般化線形モデル)などの回帰モデルオブジェクトに対して適用できます。
今回は、glmオブジェクトに適用し、segmented.glmメソッドが実行されるシミュレーションを行います。
segmented関数の引数について
segmented.defaultメソッドの主な引数は以下の通りです。segmented.glmも内部でこちらを利用します。
library(segmented)
segmentedfunction (obj, seg.Z, psi, npsi, fixed.psi = NULL, control = seg.control(),
model = TRUE, ...)
{
UseMethod("segmented")
}
<bytecode: 0x000001255cab6650>
<environment: namespace:segmented>methods(segmented)[1] segmented.Arima segmented.default segmented.glm segmented.lm segmented.lme segmented.numeric
see '?methods' for accessing help and source code2つの関数egmented.default と segmented.glm の引数は同じであることを確認します。
args(getS3method(f = "segmented", class = "glm"))
args(getS3method(f = "segmented", class = "default"))function (obj, seg.Z, psi, npsi, fixed.psi = NULL, control = seg.control(),
model = TRUE, keep.class = FALSE, ...)
NULL
function (obj, seg.Z, psi, npsi, fixed.psi = NULL, control = seg.control(),
model = TRUE, keep.class = FALSE, ...)
NULLobj:対象となる、フィット済みの
glmモデルオブジェクトを指定します。この引数には、glm(y ~ x1 + x2, family = poisson)のようにして作成されたモデルの実行結果を渡します。segmented関数は、このobjに含まれるモデルの構造(formula、family(分布)、link(リンク関数)など)を全て引き継ぎ、その上に変化点に関するパラメータを追加して新しいモデルを構築します。seg.Z:どの説明変数の傾きが変化するのかを、
~から始まる片側formula形式で指定します。例えば、objのモデル式がy ~ x1 + x2で、x1に対する応答のトレンドだけが途中で変化すると考える場合は、seg.Z = ~x1と指定します。x1とx2の両方で傾きが変化する可能性がある場合はseg.Z = ~x1 + x2とします。ここで指定する変数は、必ずobjのモデル式に元々含まれている必要があります。psi:変化点の位置に関する初期値を数値ベクトルまたはリストで指定します。
segmentedは反復計算によって最適な変化点の位置を探索するため、その計算の出発点となる「おおよその位置」を教える必要があります。-
seg.Z = ~x1のように変数が1つの場合:psi = 50やpsi = c(30, 70)のように数値ベクトルで指定します。 -
seg.Z = ~x1 + x2のように変数が複数の場合:psi = list(x1 = 50, x2 = c(45, 60))のように、変数名を付けたリストで指定します。
良い初期値を与えることは、モデルを安定して、かつ高速に収束させる上で非常に重要です。
-
npsi:psiの代替として使用します。変化点の具体的な位置の代わりに、推定したい変化点の個数を整数またはリストで指定します。psiとして適切な初期値が不明な場合に利用します。segmentedは、seg.controlで設定されたK個のグリッドを基に、内部で最適な初期値を探索します。psiと同様に、複数の変数に対しては名前付きリストで指定します(例:npsi = list(x1 = 1, x2 = 2))。psiとnpsiのどちらか一方のみを指定します。fixed.psi = NULL:推定するのではなく、固定したい変化点の位置を数値またはリストで指定します。
psiで指定した変化点はアルゴリズムによって最適化されますが、fixed.psiで指定した値は固定された定数として扱われ、その位置は変化しません。例えば、特定の政策が導入された時点など、変化点の位置が理論的に既知である場合に、その影響(傾きの変化量)だけを推定したい際に利用します。control = seg.control():フィッティングアルゴリズムの挙動を制御する詳細なパラメータを、
seg.control()関数の実行結果(リスト)として渡します。最大反復回数(it.max)、収束判定の許容誤差(tol)、計算過程の表示(display)など、多数の項目を調整できます。model = TRUE:論理値です。
TRUE(デフォルト)の場合、返されるモデルオブジェクトの中に、モデルの構築に使用されたデータ(モデルフレーム)が含まれます。これにより、オブジェクトのサイズは大きくなりますが、後からpredict関数などを利用できるようになります。keep.class = FALSE:論理値です。
segmentedが返すオブジェクトは、通常"segmented"という新しいクラスが付与されます(例:c("segmented", "glm", "lm"))。しかし、keep.class = TRUEに設定すると、この"segmented"クラスを付与せず、元のglmオブジェクトのクラス構造を維持しようとします。plot.segmentedやsummary.segmentedといった専用のメソッドが機能しなくなります。...:その他の引数を指定します。
segmented.glmメソッドでは、ここで指定された引数は内部で呼び出されるsegmented.defaultメソッドに渡されます。ですので、segmented.defaultに存在するもののsegmented.glmの引数リストには明記されていないような、よりマイナーな引数を指定する際に利用します。
シミュレーション
次に、segmented関数を確認するためのシミュレーションを行います。ここでは、segmented.glmメソッドが実行されるように、応答変数がカウントデータであるポアソン回帰モデルを扱います。
1. パッケージの読み込みとサンプルデータの作成
始めに、シミュレーションに必要なsegmentedパッケージを読み込みます。
次に、ポアソン分布に従うカウントデータを作成します。データの期待値(平均発生回数)が、ある点(x = 60)を境にして、対数線形モデルの傾きが変化するようなサンプルデータを生成します。
# パッケージを読み込みます
library(segmented)
# 再現性を確保するために乱数のシードを固定します
seed <- 20251028
set.seed(seed)
# GLM(ポアソン回帰)のためのサンプルデータ作成
# 説明変数xを作成します
x <- 1:120
# 構造変化が発生する真の変化点を設定します
true_bp <- 60
cat(paste("設定した真の変化点:", true_bp, "\n\n"))
# 変化点を境に傾きが変わる対数リンク関数を定義します
# ポアソン回帰では、応答変数の期待値の対数が線形モデルに従うと仮定します
log_lambda <- numeric(length(x))
# レジーム1 (x <= 60): 傾きが0.05
intercept <- 1.5
slope1 <- 0.05
log_lambda[x <= true_bp] <- intercept + slope1 * x[x <= true_bp]
# レジーム2 (x > 60): 傾きが-0.03に変化
# 連続性を保つように切片を調整します
slope2 <- -0.03
start_val_regime2 <- intercept + slope1 * true_bp
log_lambda[x > true_bp] <- start_val_regime2 + slope2 * (x[x > true_bp] - true_bp)
# 対数リンク関数から期待値lambdaを計算します
lambda <- exp(log_lambda)
# 期待値lambdaを持つポアソン分布から、応答変数y(カウントデータ)を生成します
y <- rpois(length(x), lambda = lambda)
# 作成したデータをデータフレームにまとめます
sim_data_glm <- data.frame(x = x, y = y)
cat("--- サンプルデータの一部を確認 ---\n")
print(str(sim_data_glm))設定した真の変化点: 60
--- サンプルデータの一部を確認 ---
'data.frame': 120 obs. of 2 variables:
$ x: int 1 2 3 4 5 6 7 8 9 10 ...
$ y: int 4 7 7 3 8 8 6 5 6 7 ...
NULL2. データの可視化と初期モデルの構築
まず、作成したデータがどのようなものか、散布図を描いて確認します。その後、segmented関数に渡すための、変化点を考慮しない標準的なポアソン回帰モデルをglm()で構築します。
# データをプロットして視覚的に確認します
plot(sim_data_glm$x, sim_data_glm$y,
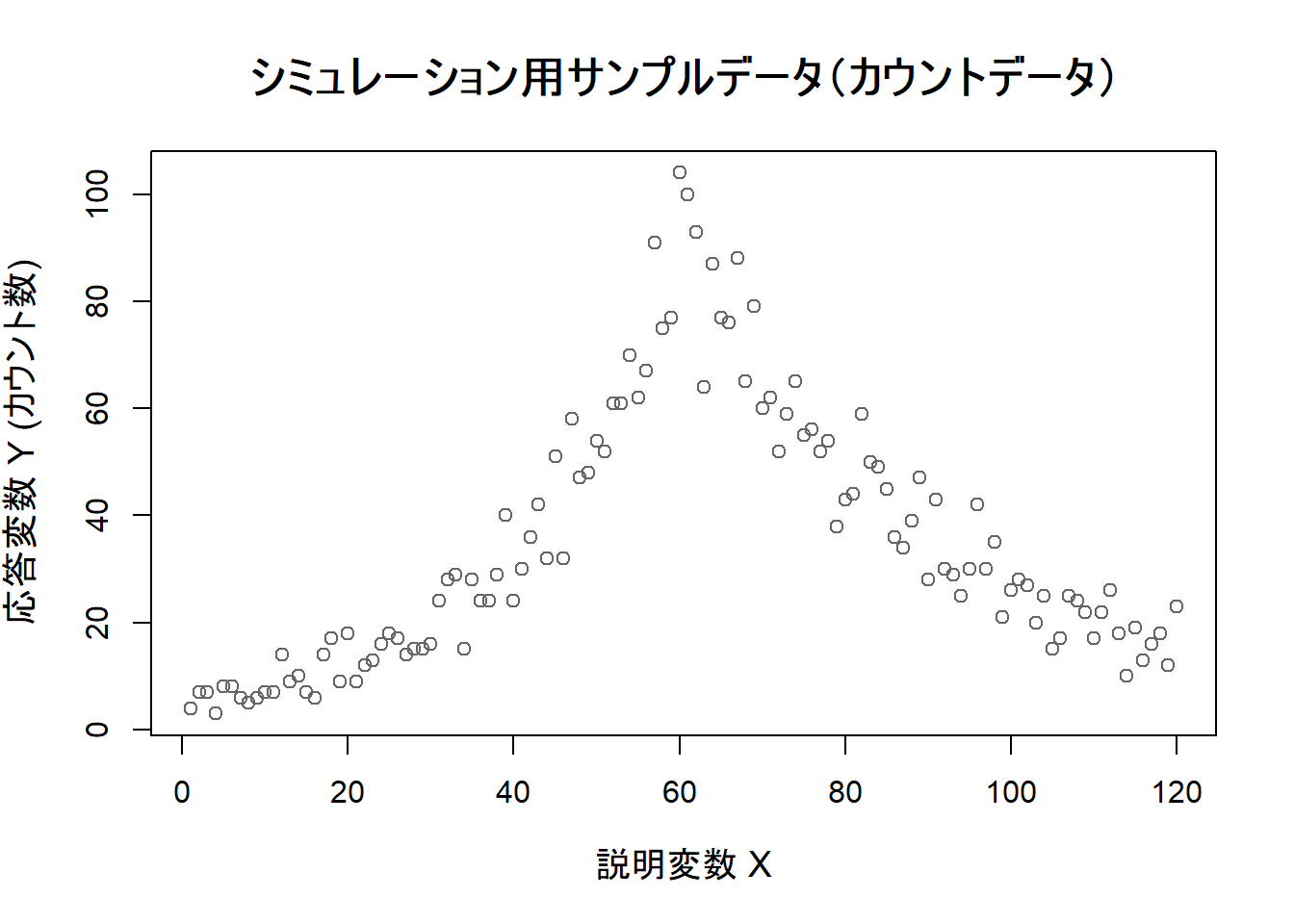
main = "シミュレーション用サンプルデータ(カウントデータ)",
xlab = "説明変数 X",
ylab = "応答変数 Y (カウント数)",
pch = 1, col = "gray40",
cex.main = 1.5, cex.lab = 1.2
)Figure 1 により、xが60付近で、カウント数の増加トレンドが減少トレンドに転じていることを確認できます。
# 変化点を考慮しない初期GLMの構築
# 始めに、変化点のない単純なポアソン回帰モデルを構築します
# y ~ x の関係をポアソン分布でモデル化します
glm_model <- glm(y ~ x, data = sim_data_glm, family = poisson)
cat("--- 初期モデルの係数 ---\n")
print(coef(glm_model))--- 初期モデルの係数 ---
(Intercept) x
3.261868565 0.004623689 3. segmented関数の適用と結果の確認
glm()で作成した初期モデルオブジェクトをsegmented関数に渡して、ポアソン回帰モデルを推定します。
seg.Zでxの傾きが変化することを指定し、psiで変化点の初期値を真の値(60)から少しずらした55に設定します。
# segmented関数による変化点の推定
# glm_modelを元に、xに関する変化点を推定します
# 変化点の初期値を55と設定します
seg_model <- segmented(glm_model, seg.Z = ~x, psi = 55)
# 結果の要約を表示します
cat("--- `summary(seg_model)` の出力 ---\n")
summary(seg_model)--- `summary(seg_model)` の出力 ---
***Regression Model with Segmented Relationship(s)***
Call:
segmented.glm(obj = glm_model, seg.Z = ~x, psi = 55)
Estimated Break-Point(s):
Est. St.Err
psi1.x 60.385 0.628
Coefficients of the linear terms:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.510223 0.077269 19.55 <2e-16 ***
x 0.049478 0.001687 29.33 <2e-16 ***
U1.x -0.079979 0.002106 -37.99 NA
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 1925.84 on 119 degrees of freedom
Residual deviance: 118.44 on 116 degrees of freedom
AIC: 741.97
Boot restarting based on 6 samples. Last fit:
Convergence attained in 1 iterations (rel. change 4.1323e-13)出力は、segmented関数によって推定されたポアソン回帰モデルの結果を要約したものです。
主に「変化点の推定値」、「各区間の回帰係数」、「モデル全体の適合度」の3つのパートから構成されています。
1. 最適な変化点の推定
Estimated Break-Point(s):
Est. St.Err
psi1.x 60.385 0.628このパートは、モデルが推定した構造変化点(ブレークポイント)に関する情報です。
psi1.x:変化点パラメータの名前です。「
xとの関係における1番目の変化点(psi)」を意味します。Est.(Estimate):推定された変化点の位置です。結果は 60.385 となっています。今回のシミュレーションでは、真の変化点を60に設定しましたので、モデルが変化点の位置を特定できたことがわかります。
St.Err(Standard Error):推定値の標準誤差です。この値が小さいほど、変化点の推定がより精確であることを示します。
2. 回帰係数の解釈
Coefficients of the linear terms:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.510223 0.077269 19.55 <2e-16 ***
x 0.049478 0.001687 29.33 <2e-16 ***
U1.x -0.079979 0.002106 -37.99 NA この表は、モデルの各回帰係数の推定値を示しています。ポアソン回帰ですので、これらの係数は対数スケールでの関係性を表します。
(Intercept):最初の区間における切片です。
x = 0のときの対数期待値の推定値が1.510であることを示します。x:最初の区間(変化点まで)の傾きです。推定値は 0.0495 となっています。これは、
xが1単位増加するごとに対数期待値が約0.0495増加することを意味します。データ作成時に設定した最初の傾き0.05と、ほぼ一致する値が推定されています。U1.x:segmentedモデルに特有の係数です。これは2番目の区間の傾きそのものではなく、変化点における傾きの「変化量」を示します。推定値は -0.0800 です。 ですので、2番目の区間(変化点以降)の実際の傾きは、最初の区間の傾きと、この変化量を足し合わせることで計算できます。0.0495 + (-0.0800) = -0.0305この計算結果は、データ作成時に設定した2番目の傾き
-0.03と、こちらもほぼ一致しており、モデルが各区間の関係性も正しく捉えられていることを示しています。
3. モデル全体の適合度
Null deviance: 1925.84 on 119 degrees of freedom
Residual deviance: 118.44 on 116 degrees of freedom
AIC: 741.97この部分は、構築されたモデルがどの程度データに適合しているかを示す指標です。
Null deviance:切片のみを含む最も単純なモデル(説明変数がないモデル)の逸脱度です。データが持つ全体のばらつきの大きさを表します。
Residual deviance:構築したモデルの逸脱度です。この値がNull devianceに比べて小さい(
1925.84>>118.44)ことから、このモデルがデータの変動を説明できていることがわかります。AIC(Akaike Information Criterion):モデルの当てはまりの良さと、モデルの複雑さ(パラメータ数)のバランスを考慮した指標です。異なるモデルを比較する際に用いられ、この値がより小さいモデルが良いモデルであると判断されます。
4. アルゴリズムに関する情報
Boot restarting based on 6 samples. Last fit:
Convergence attained in 1 iterations (rel. change 4.1323e-13)このメッセージは、モデルを推定する際の計算アルゴリズムに関する注記です。segmented関数は、より安定した解を見つけるために、内部でブートストラップを用いた再起動メカニズムを持っています。最終的に「Convergence attained(収束しました)」と表示されていることから、計算が問題なく完了したと判断できます。
4. 結果の可視化
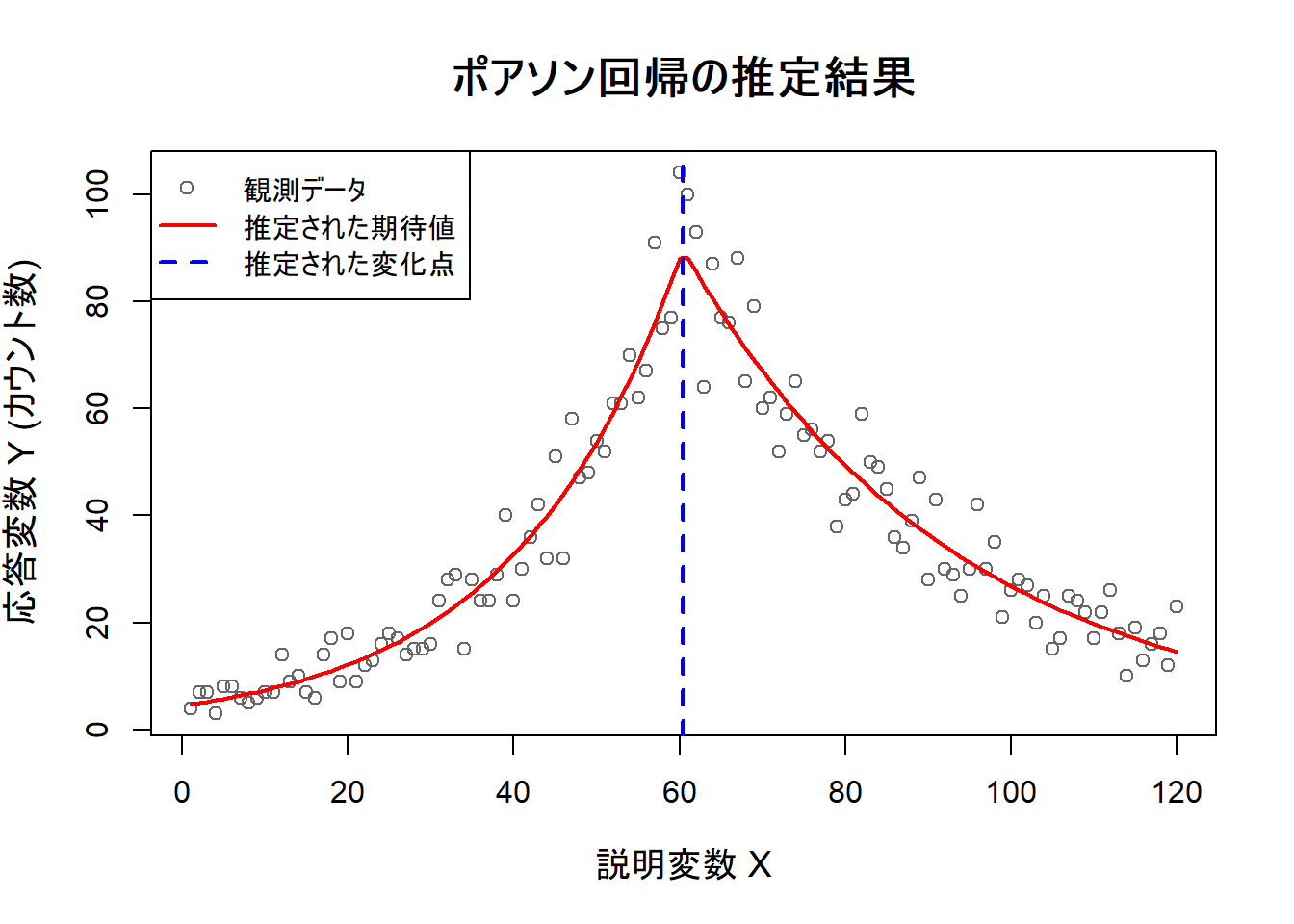
segmentedの実行結果を、plotメソッドを用いることで可視化できます。元のデータに、推定されたモデルの当てはまりと、変化点の位置を描画します。
# 1. 元のデータの散布図をプロットします
plot(sim_data_glm$x, sim_data_glm$y,
main = "ポアソン回帰の推定結果",
xlab = "説明変数 X",
ylab = "応答変数 Y (カウント数)",
pch = 1, col = "gray40",
cex.main = 1.5, cex.lab = 1.2
)
# 2. 推定された期待値を描画します (predict関数を使用)
# predict関数に type = "response" を指定して、GLMの期待値を取得します
fitted_values_response <- predict(seg_model, type = "response")
lines(sim_data_glm$x, fitted_values_response, col = "red", lwd = 2)
# 3. 推定された変化点の位置を垂直線で描画します
bp_value <- seg_model$psi[, "Est."]
abline(v = bp_value, col = "blue", lty = 2, lwd = 2)
# 4. 凡例を追加します
legend("topleft",
legend = c("観測データ", "推定された期待値", "推定された変化点"),
col = c("gray40", "red", "blue"),
lty = c(NA, 1, 2),
pch = c(1, NA, NA),
lwd = c(NA, 2, 2),
bg = "white"
)5. 信頼区間の確認
最後に、confint関数を用いて、推定された変化点の信頼区間を数値で確認します。
# 変化点の信頼区間の計算
# confint関数を用いて、変化点パラメータの信頼区間を計算します
ci_seg <- confint(seg_model)
cat("--- `confint(seg_model)` の出力 ---\n")
print(ci_seg)--- `confint(seg_model)` の出力 ---
Est. CI(95%).low CI(95%).up
psi1.x 60.3846 59.1411 61.628psi1.xの行が、変化点の信頼区間を示しています。
今回の結果では、95%信頼区間が [59.1411,61.628] となっており、真の変化点である60を区間内に含んでいます。
以上です。