Rの関数から segmented {segmented}:ARIMAモデルの場合 を確認します。
本ポストはこちらの続きです。

segmented関数について
segmented関数は、回帰モデルにおける説明変数と応答変数の関係が、ある点を境に変化するような Broken-Line Relationships を推定するためのツールです。
なお、下記引用のとおり、パッケージsegmentedの作者の論文に piecewise linear とありますため、以降本ポストでは Broken-Line Relationships を 区分線形関係 と呼称します。
Segmented or broken-line models are regression models where the relationships between the response and one or more explanatory variables are piecewise linear, namely represented by two or more straight lines connected at unknown values: these values are usually referred as breakpoints, changepoints or even joinpoints. Hereafter we use such words indistinctly.
出典:https://journal.r-project.org/articles/RN-2008-004/RN-2008-004.pdf
本関数は、変化点(ブレークポイント)をモデルのパラメータとして扱い、反復計算アルゴリズムを用いてその最適値を推定します。
変化点のおおよその初期値を与えることで、関数はモデルの対数尤度を最大化するような、最も当てはまりの良い変化点の位置と各区間の傾きを同時に見つけ出します。
segmentedはジェネリック関数であり、lm(線形モデル)やglm(一般化線形モデル)といった基本的な回帰モデルだけでなく、時系列モデルであるArimaオブジェクトなど、様々なモデルに適用可能です。
それぞれのモデルクラスに対応した専門のメソッド(segmented.lm, segmented.glm, segmented.Arimaなど)が用意されており、引数のモデルオブジェクトに応じて適切なメソッドが自動的に実行されます。
segmented関数の引数について
ジェネリック関数segmented及びその主要なメソッド(segmented.default, segmented.glm, segmented.Arima)で共通して用いられる引数は以下の通りです。
obj:区分線形関係を当てはめる対象となる、フィット済みのモデルオブジェクトを指定します。
lm()、glm()、またはarima()といった関数の実行結果がこの引数に渡されます。seg.Z:傾きの変化を許容する説明変数(共変量)を、
~ x1 + x2のようなformula形式で指定します。segmentedは、ここで指定された変数の係数が、ある変化点を境に変化するようなモデルを構築します。psi:変化点の位置に関する初期値を数値ベクトルまたはリストで指定します。アルゴリズムが最適解を見つけるための探索開始点であり、安定した収束のために適切な初期値を与えることが重要です。
npsi:psiの代わりに、推定したい変化点の個数を指定します。初期値が不明な場合に、アルゴリズムが内部で初期値を探索します。fixed.psi = NULL:推定するのではなく、位置を固定したい変化点を指定します。変化点の位置が既知である場合に、その点での傾きの変化量のみを推定したい際に利用します。
control = seg.control():seg.control()関数を用いて、フィッティングアルゴリズムの挙動を制御する詳細なパラメータ(最大反復回数、収束許容誤差など)を指定します。model = TRUE:論理値です。
TRUEの場合、結果のオブジェクトにモデルフレームを含めます。
segmented.Arimaメソッドのシミュレーション
本メソッドは、ARIMAモデルの外部共変量(xreg)に対する応答の仕方が、時系列の途中で変化するような状況をモデル化するために使用されます。
segmented.Arimaは、内部でU(傾きの変化を表す変数)やV(推定アルゴリズムで用いる変数)といった新しい共変量を動的に作成し、update()関数を用いてxregを更新しながら繰り返しarima()を呼び出すことで、最適な変化点を探索します。
1. パッケージの読み込みとサンプルデータの作成
始めに、segmentedパッケージを読み込みます。
次に、ARIMAモデルに従う時系列データを作成します。
このデータは、自己回帰的な構造(AR(1))を持つ誤差項と、ある外部変数xへの依存関係から構成されるものとします。
そして、xが時系列yに与える影響(傾き)が、70番目の時点を境に変化するように設定します。
# パッケージを読み込みます
library(segmented)
# 再現性を確保するために乱数のシードを固定します
seed <- 20251030
set.seed(seed)
# segmented.Arimaのためのサンプルデータ作成
# データ全体の観測数を設定します
n <- 150
# 外部共変量xを作成します (例えば、時間経過や何らかの介入量)
x <- 1:n
# 構造変化が発生する真の変化点を設定します
true_bp <- 70
cat(paste("設定した真の変化点:", true_bp, "\n\n"))
# 変化点を境にxの係数(傾き)が変わる潜在的な関係を定義します
y_latent <- numeric(n)
intercept <- 10
slope1 <- 0.8 # 最初の区間の傾き
y_latent[1:true_bp] <- intercept + slope1 * x[1:true_bp]
slope2 <- -0.5 # 2番目の区間の傾き
# 連続性を保つように2番目の区間の開始値を計算します
start_val_regime2 <- intercept + slope1 * true_bp
y_latent[(true_bp + 1):n] <- start_val_regime2 + slope2 * (x[(true_bp + 1):n] - true_bp)
# AR(1)構造を持つ誤差項を生成します
# y_t = y_latent_t + error_t, error_t = 0.6 * error_{t-1} + innovation_t
ar_error <- arima.sim(model = list(ar = 0.6), n = n, sd = 5)
# 最終的な時系列データyを生成します
y <- y_latent + ar_error
# 作成したデータをデータフレームにまとめます
sim_data_arima <- data.frame(y = y, x = x)
cat("--- サンプルデータの一部を確認 ---\n")
print(str(sim_data_arima))設定した真の変化点: 70
--- サンプルデータの一部を確認 ---
'data.frame': 150 obs. of 2 variables:
$ y: Time-Series from 1 to 150: 10.04 6.08 11.67 14.85 8.73 ...
$ x: int 1 2 3 4 5 6 7 8 9 10 ...
NULL2. データの可視化と初期ARIMAモデルの構築
作成したデータの関係性を視覚的に確認します。
その後、segmented関数に渡すための、変化点を考慮しない標準的なARIMAモデルをarima()で構築します。
この際、xを外部共変量としてxreg引数で指定します。
# yとxの関係をプロットして視覚的に確認します
plot(sim_data_arima$x, sim_data_arima$y,
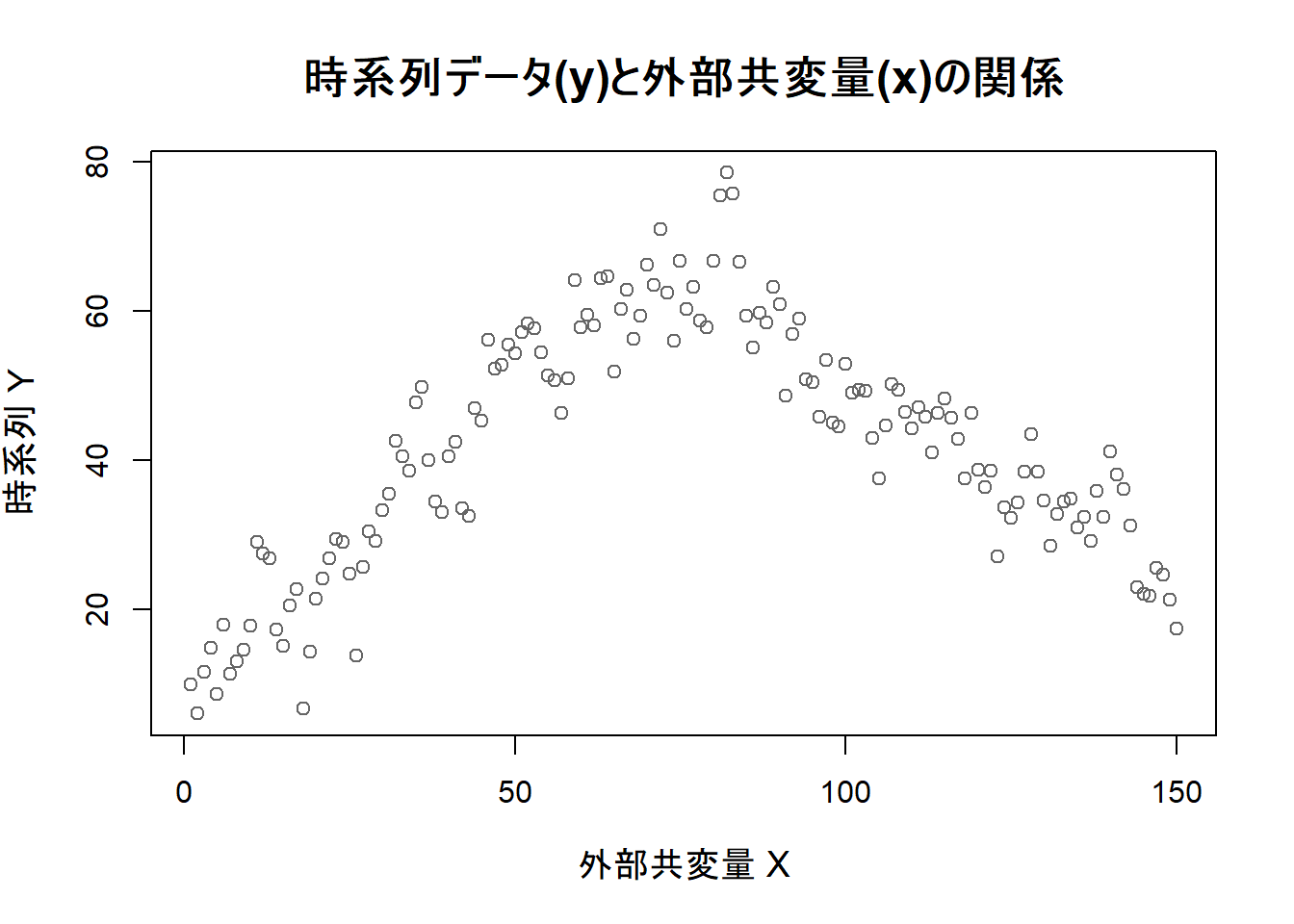
main = "時系列データ(y)と外部共変量(x)の関係",
xlab = "外部共変量 X",
ylab = "時系列 Y",
pch = 1, col = "gray40",
cex.main = 1.5, cex.lab = 1.2
)xが70付近で、yの増加トレンドが減少トレンドに転じていることを確認できます。
3. segmented.Arimaの適用と結果の確認
arima()で作成した初期モデルオブジェクトをsegmented関数に渡します。
objのクラスがArimaであるため、segmented.Arimaメソッドが自動的に実行されます。
seg.Zでxの傾きが変化することを指定し、psiで変化点の初期値を65と設定します。
# 変化点を考慮しない初期ARIMAモデルの構築
# 始めに、xを外部共変量として含む、変化点のないARIMAモデルを構築します
# データ生成過程に基づき、AR(1)モデルを指定します
# xreg引数で、外部からの影響をモデルに組み込みます
xreg_matrix <- as.matrix(sim_data_arima[, "x", drop = FALSE])
colnames(xreg_matrix) <- "x"
arima_model <- arima(sim_data_arima$y, order = c(1, 0, 0), xreg = xreg_matrix)
print(arima_model)
Call:
arima(x = sim_data_arima$y, order = c(1, 0, 0), xreg = xreg_matrix)
Coefficients:
ar1 intercept x
0.9451 31.5948 0.0657
s.e. 0.0276 13.4244 0.1442
sigma^2 estimated as 32.44: log likelihood = -474.92, aic = 957.84この出力は、segmented関数を適用する前段階として構築した、変化点を考慮しない初期ARIMAモデルの分析結果を要約したものです。
このモデルは、「時系列データyは、自己回帰的な構造を持ち、かつ、外部共変量xと単一の線形関係を持つ」と仮定しています。
この結果は、後ほど実行する区分線形モデルと比較するための基準(ベースライン)となります。
1. Call: (モデルの呼び出し)
Call:
arima(x = sim_data_arima$y, order = c(1, 0, 0), xreg = xreg_matrix)この部分は、このモデルを生成するために実行されたRのコマンドそのものを示しています。
x = sim_data_arima$y:モデル化の対象となっている時系列データを指定しています。
order = c(1, 0, 0):ARIMAモデルの次数(p, d, q)を指定しており、モデルの根幹を定義します。
-
p = 1: 自己回帰 (AR) の次数が1であることを示します。これは、時系列の現在の値が、1期前の過去の値に依存する構造(AR(1)モデル)を持つことを意味します。 -
d = 0: 和分 (I) の次数が0であることを示します。これは、時系列データに対して階差(差分)を取る処理を行っていないことを意味します。 -
q = 0: 移動平均 (MA) の次数が0であることを示します。
ですので、このモデルは時系列の誤差構造としてAR(1)モデルを仮定しています。
-
xreg = xreg_matrix:モデルに外部共変量(説明変数)が含まれていることを示します。今回のケースでは、
xという変数がyに影響を与えていると仮定しています。
2. Coefficients: (推定された係数)
Coefficients:
ar1 intercept x
0.9451 31.5948 0.0657
s.e. 0.0276 13.4244 0.1442この表は、モデルの各パラメータの推定値とその標準誤差(s.e.)を示しています。
ar1:AR(1)モデルの自己回帰係数(φ)の推定値です。
0.9451という値は1に近く、時系列の誤差項に強い正の自己相関があること(つまり、前期の誤差が今期の誤差に強く影響すること)を示唆しています。xの効果を単一の直線で当てはめようとした結果、データ生成時の設定(ar = 0.6)とは異なっています。intercept:モデルの切片の推定値です。
x=0のときのyの期待値を表します。x:外部共変量
xの係数(傾き)の推定値です。0.0657という値は、データ全期間を通じての平均的なxの効果を示しています。このモデルは変化点を考慮していないため、増加トレンドと減少トレンドが混ざり合った結果です。s.e.(Standard Error):各係数の推定値の標準誤差です。推定の精度を示し、この値が小さいほど、その係数の推定がより信頼できることを意味します。
3. モデル全体の適合度
sigma^2 estimated as 32.44: log likelihood = -474.92, aic = 957.84この部分は、モデルがどの程度データに適合しているかを示す統計指標です。
sigma^2 estimated as 32.44:モデルの残差(予測できなかった部分)の分散の推定値です。この値が小さいほど、モデルがデータの変動をより多く説明できていることを意味します。
log likelihood = -474.92:対数尤度です。モデルの当てはまりの良さを示す指標で、この値を最大化するようにパラメータが推定されます。
aic = 957.84:赤池情報量規準(AIC)です。モデルの当てはまりの良さと、モデルの複雑さ(パラメータ数)のバランスを評価します。この値が小さいほど、より良いモデルであると判断されます。この
957.84というAICの値が、後でsegmentedモデルのAICと比較され、モデルが改善したかどうかを判断するための基準となります。
# segmented.Arimaによる変化点の推定
# arima_modelを元に、共変量xに関する変化点を推定します
# 変化点の初期値を65と設定します
seg_arima_model <- segmented(arima_model, seg.Z = ~x, psi = list(x = 65))
print(seg_arima_model)Call: segmented.Arima(obj = arima_model, seg.Z = ~x, psi = list(x = 65))
Coefficients of the linear terms:
ar1 intercept x U1.x
0.4983 8.4459 0.8162 -1.3791
Estimated Break-Point(s):
psi1.x
72
sigma^2 estimated as 24.44: log likelihood = -452.69, aic = 917.39この出力は、segmented関数による分析の結果であり、変化点を導入したARIMAモデルの要約です。
初期のARIMAモデルと比較することで、モデルがどの程度改善されたかを評価できます。
1. Call: (モデルの呼び出し)
Call: segmented.Arima(obj = arima_model, seg.Z = ~x, psi = list(x = 65))この部分は、このモデルを生成するために実行されたコマンドを示しています。
arima_modelという初期モデルに対し、外部共変量xに関する変化点を、初期値65から探索を開始して推定したことが記録されています。
objのクラスがArimaであったため、segmented.Arimaメソッドが正しく呼び出されました。
2. Coefficients of the linear terms: (回帰係数の解釈)
Coefficients of the linear terms:
ar1 intercept x U1.x
0.4983 8.4459 0.8162 -1.3791 ar1:AR(1)モデルの自己回帰係数の推定値です。
0.4983という値は、初期モデルで推定された0.9451よりも小さくなっています。初期モデルでは、xの効果の変化を単一の直線で表現しようとしたため、説明しきれない変動が誤差項に残り、見かけ上の自己相関が過大に推定されていました。変化点を導入したことで、xの効果が正しくモデル化され、誤差項の自己相関がより適切に(データ生成時の0.6に近い値で)推定されるようになりました。intercept:最初の区間における切片の推定値です。
x:最初の区間(変化点まで)における
xの傾きです。推定値は0.8162となっており、データ生成時に設定した最初の傾き0.8を捉えています。U1.x:segmentedモデル特有の係数で、変化点における傾きの「変化量」を示します。推定値は-1.3791です。ですので、2番目の区間(変化点以降)の傾きは、以下のように計算されます。(最初の区間の傾き) + (傾きの変化量) = 0.8162 + (-1.3791) = -0.5629この計算結果は、データ生成時に設定した2番目の傾き
-0.5と近い値であり、モデルが区分ごとの関係性も正しく推定できていることを示します。
3. Estimated Break-Point(s): (変化点の推定)
Estimated Break-Point(s):
psi1.x
72 psi1.x:xとの関係における1番目の変化点の推定値を示します。結果は72と推定されました。データ生成時に設定した真の変化点は70でしたので、モデルが時系列データのノイズの中から、ほぼ構造変化のタイミングを特定できたことがわかります。
4. モデル全体の適合度
sigma^2 estimated as 24.44: log likelihood = -452.69, aic = 917.39この部分は、モデル全体の当てはまりの良さを示す指標です。
sigma^2(残差分散):24.44という値は、初期モデルの32.44よりも小さくなっています。これは、モデルの予測誤差が減少し、データへの適合度が向上したことを意味します。log likelihood(対数尤度):-452.69という値は、初期モデルの-474.92よりも大きくなっており(より0に近く)、当てはまりが良くなったことを示します。aic(赤池情報量規準):917.39という値は、初期モデルのAIC957.84と比較して減少しています。AICは、モデルの複雑さを考慮した上で当てはまりの良さを評価する指標です。AICが減少したということは、「変化点を導入するというモデルの複雑化は、それを補って余りあるほど当てはまりを改善した」ということを意味し、区分線形モデルの方が、単一の線形モデルよりも適切であることを示しています。
4. 結果の可視化
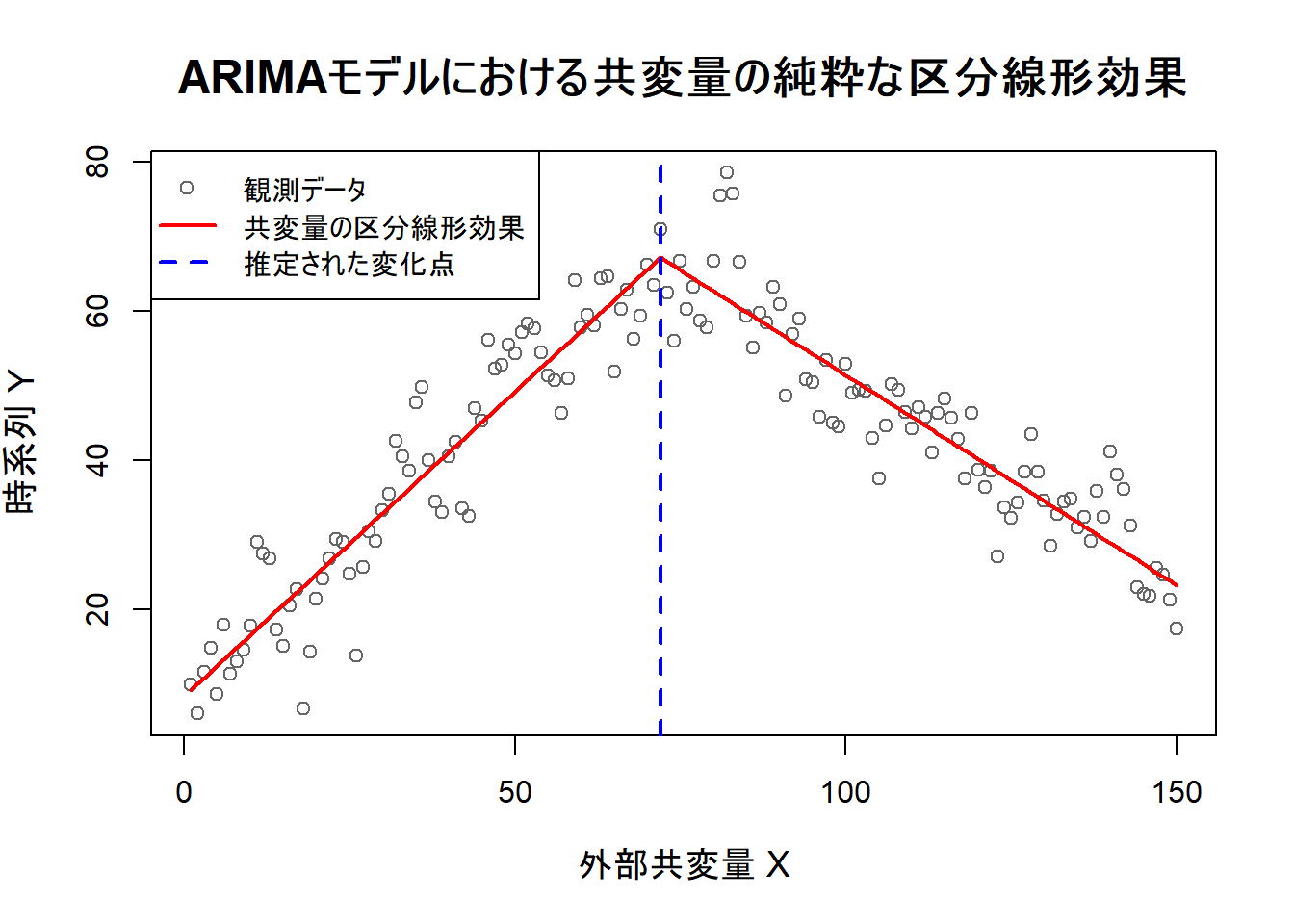
segmentedの実行結果を可視化します。元のデータに対し、推定された区分線形関係を重ねて描画します。
ARIMAモデルの場合、時系列の自己相関部分と共変量の効果が合わさってyが生成されるため、共変量の効果のみを抽出して可視化します。
# 1. 元のデータの散布図をプロットします
plot(sim_data_arima$x, sim_data_arima$y,
main = "ARIMAモデルにおける共変量の純粋な区分線形効果",
xlab = "外部共変量 X",
ylab = "時系列 Y",
pch = 1, col = "gray40",
cex.main = 1.5, cex.lab = 1.2
)
# 2. モデルから必要なパラメータを抽出します
# ==========================================
# 係数を取得します
model_coefs <- seg_arima_model$coef
# 変化点の推定値を取得します
breakpoint <- seg_arima_model$psi[, "Est."]
# 係数を個別の変数に格納します
intercept_hat <- model_coefs["intercept"]
slope1_hat <- model_coefs["x"]
slope_change_hat <- model_coefs["U1.x"]
# 3. 区分線形成分の値を格納するためのベクトルを用意します
# =======================================================
x_effect <- numeric(length(sim_data_arima$x))
# 4. 2つのセグメントに分けて、それぞれの期待値を計算します
# ========================================================
# 最初のセグメント (変化点まで)
indices1 <- sim_data_arima$x <= breakpoint
x_effect[indices1] <- intercept_hat + slope1_hat * sim_data_arima$x[indices1]
# 2番目のセグメント (変化点以降)
indices2 <- sim_data_arima$x > breakpoint
x_effect[indices2] <- intercept_hat + slope1_hat * sim_data_arima$x[indices2] +
slope_change_hat * (sim_data_arima$x[indices2] - breakpoint)
# 5. 計算した区分線形成分をプロットします
# =========================================
lines(sim_data_arima$x, x_effect, col = "red", lwd = 2)
# 6. 推定された変化点の位置に、青い破線の垂直線を引きます
abline(v = breakpoint, col = "blue", lty = 2, lwd = 2)
# 7. 凡例を追加します
# ===================
legend("topleft",
legend = c("観測データ", "共変量の区分線形効果", "推定された変化点"),
col = c("gray40", "red", "blue"),
lty = c(NA, 1, 2),
pch = c(1, NA, NA),
lwd = c(NA, 2, 2),
bg = "white"
)5. 信頼区間の確認
95%信頼区間は以下の式で計算されます。
95%信頼区間 = 推定値 ± 1.96 × 標準誤差
ここで、1.96は正規分布における95%の範囲をカバーするための臨界値(Z値)です。
segmentedモデルの推定値は正規分布に近似するため、この値を使用します。
seg_arima_modelオブジェクトには、この計算に必要な「推定値」と「標準誤差」の両方が含まれています。
- 推定値 (
Est.):seg_arima_model$psi[, "Est."] - 標準誤差 (
St.Err):seg_arima_model$psi[, "St.Err"]
これらを使って、以下のよう計算します。
# 1. モデルオブジェクトから必要な値を抽出します
bp_estimate <- seg_arima_model$psi[, "Est."]
bp_std_error <- seg_arima_model$psi[, "St.Err"]
cat(paste("推定された変化点:", round(bp_estimate, 3), "\n"))
cat(paste("標準誤差:", round(bp_std_error, 3), "\n\n"))
# 2. 95%信頼区間の臨界値(Z値)を設定します
critical_value <- qnorm(0.975) # 約1.96になります
# 3. 信頼区間の下限値と上限値を計算します
lower_bound <- bp_estimate - critical_value * bp_std_error
upper_bound <- bp_estimate + critical_value * bp_std_error
# 4. 結果をまとめて表示します
ci_matrix <- matrix(c(lower_bound, upper_bound), nrow = 1)
colnames(ci_matrix) <- c("2.5 %", "97.5 %")
rownames(ci_matrix) <- "psi1.x"
cat("--- 計算された95%信頼区間 ---\n")
print(ci_matrix)推定された変化点: 72
標準誤差: 2.139
--- 計算された95%信頼区間 ---
2.5 % 97.5 %
psi1.x 67.80756 76.19255以上です。