Rの関数から ur.df {urca} を確認します。
本ポストはこちらの続きです。

ur.df関数について
ur.df関数は、tseriesパッケージのadf.testと同様に、拡張ディッキー–フラー検定(Augmented Dickey-Fuller Test) を実行するための関数です。この関数の目的は、時系列データに単位根が存在するかどうかを検定すること、すなわち時系列が非定常か定常(もしくはトレンド定常)かを判断することです。
adf.test関数と比較して、ur.df関数はより高機能で柔軟です。特に、検定の前提となるモデルを明確に指定できる点や、ラグ選択を情報量規準により設定する機能、そして検定結果が詳細に出力される点が大きな特徴です。
検定の帰無仮説は一貫して「単位根が存在する(時系列は非定常である)」です。
ur.df関数の引数について
library(urca)
args(ur.df)function (y, type = c("none", "drift", "trend"), lags = 1, selectlags = c("Fixed",
"AIC", "BIC"))
NULLy
検定の対象となる時系列データを指定します。数値ベクトルやtsオブジェクトなどが該当します。
type
この引数は検定に使用する回帰モデルを指定する引数です。時系列データの形状や背景知識に基づいて、以下の3つから適切なモデルを選択します。
-
"none": 定数項(ドリフト)もトレンドも含まないモデルで検定します。- 検定方程式: Δyₜ = γyₜ₋₁ + … + εₜ
- 時系列がゼロを中心としてランダムウォークしているような場合に選択します。
-
"drift": 定数項(ドリフト)を含むが、トレンドは含まないモデルで検定します。- 検定方程式: Δyₜ = α + γyₜ₋₁ + … + εₜ
- 時系列がゼロではない一定の平均値の周りでランダムウォークしているように見える(ドリフト付きランダムウォーク)場合に選択します。
-
"trend": 定数項(ドリフト)と時間のトレンド項の両方を含むモデルで検定します。- 検定方程式: Δyₜ = α + βt + γyₜ₋₁ + … + εₜ
- 時系列が時間経過とともに増加または減少する明確な傾向(トレンド)の周りで変動しているように見える場合に選択します。この場合の対立仮説は「トレンド周りで定常(トレンド定常)」となります。
lags
検定モデルに含めるラグ次数を整数で指定します。これは、selectlags = "Fixed" の場合にのみ有効です。
selectlags
ラグ次数をどのように決定するかを指定します。
-
"Fixed"(デフォルト):lags引数で指定された固定の次数を使用します。 -
"AIC": 赤池情報量規準 (AIC) が最小になるように、最適なラグ次数を自動的に選択します。 -
"BIC": ベイズ情報量規準 (BIC) が最小になるように、最適なラグ次数を自動的に選択します。
シミュレーション
ur.df関数の挙動、特にtype引数の設定による差異を確認するために、それぞれのtypeに対応する3種類のサンプルデータを生成し、検定を実行します。
なお、有意水準は5%とします。
# 再現性を確保するために乱数のシードを設定します
seed <- 20251010
set.seed(seed)
# シミュレーションのためのサンプルデータ作成
# データポイントの数を定義します
n <- 200
# 1. type = "none" に対応するデータ(ゼロ中心のランダムウォーク)
# type='none'用データ:ドリフトなし単位根過程
data_none <- cumsum(rnorm(n))
# 2. type = "drift" に対応するデータ(ドリフト付きランダムウォーク)
# 毎期平均0.5ずつ上昇していく単位根過程です
# type='drift'用データ:ドリフト付き単位根過程
data_drift <- cumsum(rnorm(n) + 0.5)
# 3. type = "trend" に対応するデータ(トレンド定常過程)
# 時間トレンドの周りを定常的に変動する過程です。単位根は持ちません。
# type='trend'用データ:トレンド定常過程
data_trend_stationary <- 10 + 0.8 * (1:n) + arima.sim(model = list(ar = 0.5), n = n)
# 作成したデータの可視化
# 描画デバイスを1行3列に分割します
par(mfrow = c(1, 3), mar = c(4, 4, 3, 2))
# プロット1
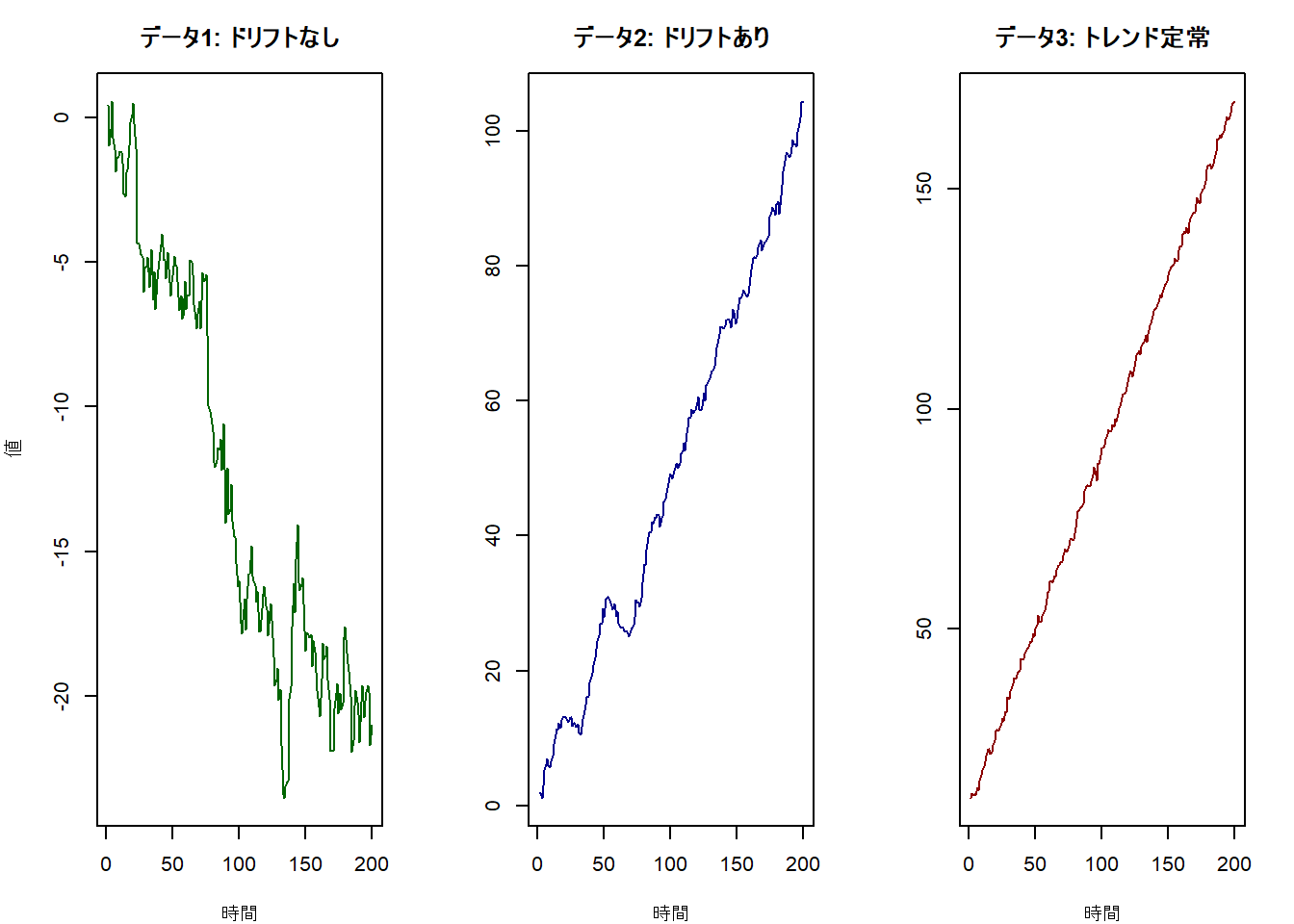
plot(data_none,
type = "l", col = "darkgreen",
main = "データ1: ドリフトなし",
xlab = "時間", ylab = "値"
)
# プロット2
plot(data_drift,
type = "l", col = "darkblue",
main = "データ2: ドリフトあり",
xlab = "時間", ylab = ""
)
# プロット3
plot(data_trend_stationary,
type = "l", col = "darkred",
main = "データ3: トレンド定常",
xlab = "時間", ylab = ""
)ケース1:ドリフトなしデータに type=‘none’ で検定
本サンプルデータは単位根を持つため、帰無仮説は棄却されないと予測されます。
ur_result_none <- ur.df(data_none, type = "none", selectlags = "AIC")
summary(ur_result_none)
###############################################
# Augmented Dickey-Fuller Test Unit Root Test #
###############################################
Test regression none
Call:
lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)
Residuals:
Min 1Q Median 3Q Max
-3.2871 -0.6976 -0.0075 0.4957 2.9120
Coefficients:
Estimate Std. Error t value Pr(>|t|)
z.lag.1 0.003414 0.004649 0.734 0.464
z.diff.lag -0.019537 0.071550 -0.273 0.785
Residual standard error: 0.9359 on 196 degrees of freedom
Multiple R-squared: 0.002918, Adjusted R-squared: -0.007256
F-statistic: 0.2868 on 2 and 196 DF, p-value: 0.751
Value of test-statistic is: 0.7342
Critical values for test statistics:
1pct 5pct 10pct
tau1 -2.58 -1.95 -1.62 ur.df検定結果の確認 (type = “none”)
この出力は、ドリフト(定数項)なしの単位根過程として生成されたdata_noneに対して、type="none"(定数項もトレンド項も含まないモデル)を指定して拡張ディッキー–フラー検定を行った結果です。
全体像
###############################################
# Augmented Dickey-Fuller Test Unit Root Test #
###############################################
Test regression none 最初の部分は、実行された検定が拡張ディッキー–フラー(ADF)単位根検定であること、そして検定に使用された回帰モデルがnoneタイプであることを示しています。
検定用の回帰モデル
Call:
lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)このCallの部分は、ur.df関数の内部で実行された具体的な回帰モデルを示しています。ADF検定は、内部的にこのような線形回帰(lm)を推定し、その結果を利用します。
-
z.diff: 応答変数(被説明変数)です。元の時系列データyの一階差分Δyₜに相当します。 -
z.lag.1: 検定の鍵となる説明変数です。元の時系列データの一期前の値yₜ₋₁に相当します。単位根の有無は、この変数の係数が0かどうかで判断されます。 -
- 1: 切片項(定数項)を含まないことを指定しています。type = "none"を選択したため、この設定になっています。 -
z.diff.lag: ラグ付けされた差分項Δyₜ₋₁,Δyₜ₋₂, … です。時系列の自己相関をモデルに含めるための項であり、この項があるため「拡張」ディッキー–フラー検定と呼ばれます。
回帰モデルの推定結果
Coefficients:
Estimate Std. Error t value Pr(>|t|)
z.lag.1 0.003414 0.004649 0.734 0.464
z.diff.lag -0.019537 0.071550 -0.273 0.785この部分は、上記の回帰モデルを推定した結果です。最も重要なのは z.lag.1 の行です。
-
Estimate:z.lag.1の係数の推定値 (γ) です。単位根が存在する場合、この係数は理論的に0になります。推定値は0.003414と0に非常に近い値です。 -
t value:z.lag.1の係数に対するt統計量です。この0.734という値が、ADF検定における検定統計量(tau statistic)そのものになります。
検定統計量と棄却限界値の比較
Value of test-statistic is: 0.7342
Critical values for test statistics:
1pct 5pct 10pct
tau1 -2.58 -1.95 -1.62出力の最終部分が、単位根検定の結論を導くための最も重要な箇所です。
Value of test-statistic is: 0.7342: ADF検定の検定統計量の値です。先に見た回帰モデルのz.lag.1のt値(0.734)と一致していることが確認できます。Critical values for test statistics:: 検定の判断基準となる棄却限界値(Critical Value)です。単位根検定の棄却限界値は、通常のt分布とは異なる特殊な分布に従うため、シミュレーションによって求められた値が用いられます。tau1はtype="none"モデルに対応する棄却限界値の名称です。-
1pct: 有意水準1%の棄却限界値 (-2.58) -
5pct: 有意水準5%の棄却限界値 (-1.95) -
10pct: 有意水準10%の棄却限界値 (-1.62)
-
結論の導出
検定の判断は、「検定統計量」と「棄却限界値」を比較して行います。
- 帰無仮説 (H₀): 単位根が存在する。
- 判断ルール:
検定統計量 < 棄却限界値であれば、帰無仮説を棄却する。
今回の結果を見てみましょう。有意水準5%で判断します。
- 検定統計量:
0.7342 - 5%棄却限界値:
-1.95
0.7342 > -1.95ですので、検定統計量は棄却限界値を下回っていません。
ですので、帰無仮説「単位根が存在する」を棄却することはできません。
この検定結果は、「この時系列データが単位根を持つ」という仮説と矛盾しないことを示しています。今回のデータは実際に単位根過程として生成したものですので、検定が正しく機能していることが確認できます。
ケース2:ドリフトありデータに type=‘drift’ で検定
こちらのデータも単位根を持つため、帰無仮説は棄却されないと予測されます。
ur_result_drift <- ur.df(data_drift, type = "drift", selectlags = "AIC")
summary(ur_result_drift)
###############################################
# Augmented Dickey-Fuller Test Unit Root Test #
###############################################
Test regression drift
Call:
lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)
Residuals:
Min 1Q Median 3Q Max
-2.52909 -0.65560 -0.01024 0.61564 2.38676
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.421359 0.144670 2.913 0.004 **
z.lag.1 0.001619 0.002508 0.646 0.519
z.diff.lag 0.031975 0.071782 0.445 0.656
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.009 on 195 degrees of freedom
Multiple R-squared: 0.003439, Adjusted R-squared: -0.006782
F-statistic: 0.3365 on 2 and 195 DF, p-value: 0.7147
Value of test-statistic is: 0.6455 19.3321
Critical values for test statistics:
1pct 5pct 10pct
tau2 -3.46 -2.88 -2.57
phi1 6.52 4.63 3.81 ur.df検定結果の確認 (type = “drift”)
この出力は、ドリフト(定数項)付きの単位根過程として生成されたdata_driftに対して、type="drift"(定数項を含むがトレンド項は含まないモデル)を指定して拡張ディッキー–フラー検定を行った結果です。
全体像
###############################################
# Augmented Dickey-Fuller Test Unit Root Test #
###############################################
Test regression drift 検定が拡張ディッキー–フラー(ADF)単位根検定であること、そして検定に使用された回帰モデルがdriftタイプであることを示しています。
検定用の回帰モデル
Call:
lm(formula = z.diff ~ z.lag.1 + 1 + z.diff.lag)このCallは、ur.df関数が内部で実行した回帰モデルを示しています。type="none"の時との違いは + 1 の部分です。
-
z.diff ~ z.lag.1 ...:type="none"と同様、Δyₜをyₜ₋₁などで回帰しています。 -
+ 1: 切片項(定数項)を含むことを指定しています。type = "drift"を選択したため、この項がモデルに追加されています。この切片項が、時系列の「ドリフト(平均的な変化量)」を捉えます。
回帰モデルの推定結果
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.421359 0.144670 2.913 0.004 **
z.lag.1 0.001619 0.002508 0.646 0.519
z.diff.lag 0.031975 0.071782 0.445 0.656 この回帰結果には、(Intercept)(切片項)が追加されています。
-
(Intercept): ドリフト項の推定値です。0.421となっており、これはサンプルデータ生成時に設定したドリフト0.5に近い値です。統計的にも有意(Pr(>|t|) = 0.004)であり、この時系列が平均的に上昇する傾向を持つことを示唆しています。 -
z.lag.1: 単位根の有無を判断するための項です。こちらの係数に対するt値0.646が、単位根検定の検定統計量になります。
検定統計量と棄却限界値の比較
Value of test-statistic is: 0.6455 19.3321
Critical values for test statistics:
1pct 5pct 10pct
tau2 -3.46 -2.88 -2.57
phi1 6.52 4.63 3.81type="drift"の場合、検定統計量と棄却限界値が2種類出力されます。これがtype="none"との大きな違いです。
- tau2統計量(単位根の検定)
-
Value of test-statistic is: 0.6455: 1つ目の値がtau2統計量です。これは回帰モデルのz.lag.1のt値(0.646)と同じ値であり、単位根の存在(γ=0)を検定するためのものです。 -
Critical values ... tau2:tau2統計量に対応する棄却限界値です。
-
- phi1統計量(ドリフトの有意性の検定)
-
Value of test-statistic is: 19.3321: 2つ目の値がphi1統計量です。こちらはF統計量の一種で、「ドリフト項は0であり、かつ、単位根が存在する(α=0, γ=0)」という同時仮説を検定するためのものです。ドリフト項を含めたこのモデルが、ドリフト項を含まないtype="none"のモデルよりも意味があるかどうかを判断するのに役立ちます。 -
Critical values ... phi1:phi1統計量に対応する棄却限界値です。
-
結論の導出
最初に、主目的である単位根の有無をtau2統計量で判断します。
- 帰無仮説 (H₀): 単位根が存在する。
- 判断ルール:
検定統計量(tau2) < 棄却限界値(tau2)であれば、帰無仮説を棄却する。
有意水準5%で判断します。
- 検定統計量 (tau2):
0.6455 - 5%棄却限界値 (tau2):
-2.88
0.6455 > -2.88ですので、検定統計量は棄却限界値を下回っていません。
ですので、帰無仮説「単位根が存在する」を棄却することはできません。 この結果は、このデータが非定常であることを示唆しています。
次に(補助的に)、phi1統計量でモデルの妥当性を確認します。
- 帰無仮説 (H₀): ドリフトは不要であり、かつ単位根が存在する。
- 判断ルール:
検定統計量(phi1) > 棄却限界値(phi1)であれば、帰無仮説を棄却する。
有意水準5%で判断します。
- 検定統計量 (phi1):
19.3321 - 5%棄却限界値 (phi1):
4.63
19.3321 > 4.63ですので、帰無仮説は棄却されます。 この結果は、「ドリフト項は0である」という部分が否定されたことを意味し、ドリフト項をモデルに含めたtype="drift"の選択は適切であったことを示唆しています。
総合的な結論: この時系列は単位根を持ち(非定常であり)、かつ統計的に有意なドリフト(定数項)を持つ、いわゆる「ドリフト付きランダムウォーク」であると結論付けられます。こちらもデータ生成時の設定と整合的な結果です。
ケース3:トレンド定常データに type=‘trend’ で検定
このデータは単位根を持たない(トレンド定常)ため、帰無仮説は棄却されると予測されます。
ur_result_trend <- ur.df(data_trend_stationary, type = "trend", selectlags = "AIC")
summary(ur_result_trend)
###############################################
# Augmented Dickey-Fuller Test Unit Root Test #
###############################################
Test regression trend
Call:
lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
Residuals:
Min 1Q Median 3Q Max
-2.99129 -0.46722 0.03611 0.55783 2.06553
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.33625 0.72458 8.745 1.07e-15 ***
z.lag.1 -0.55479 0.07340 -7.559 1.58e-12 ***
tt 0.44312 0.05861 7.561 1.56e-12 ***
z.diff.lag 0.04937 0.07153 0.690 0.491
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8698 on 194 degrees of freedom
Multiple R-squared: 0.2676, Adjusted R-squared: 0.2563
F-statistic: 23.63 on 3 and 194 DF, p-value: 4.439e-13
Value of test-statistic is: -7.5586 70.0758 28.5859
Critical values for test statistics:
1pct 5pct 10pct
tau3 -3.99 -3.43 -3.13
phi2 6.22 4.75 4.07
phi3 8.43 6.49 5.47 ur.df検定結果の確認 (type = “trend”)
この出力は、時間トレンドの周りで定常的に変動するデータとして生成されたdata_trend_stationaryに対して、type="trend"(定数項と時間トレンド項の両方を含むモデル)を指定して拡張ディッキー–フラー検定を行った結果です。
全体像
###############################################
# Augmented Dickey-Fuller Test Unit Root Test #
###############################################
Test regression trend 検定が拡張ディッキー–フラー(ADF)単位根検定であること、そして検定に使用された回帰モデルがtrendタイプであることを示しています。
検定用の回帰モデル
Call:
lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)このCallは、ur.df関数が内部で実行した回帰モデルを示しています。type="drift"のモデルに、さらに時間トレンドttが追加されています。
-
z.diff ~ z.lag.1 ...:Δyₜをyₜ₋₁などで回帰しています。 -
+ 1: 切片項(定数項)です。 -
+ tt: 時間トレンド項です。ur.df関数が内部で自動的に生成する変数で、t = 1, 2, 3, ...という時間の経過を表します。type = "trend"を選択したため、この項がモデルに追加されています。
回帰モデルの推定結果
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.33625 0.72458 8.745 1.07e-15 ***
z.lag.1 -0.55479 0.07340 -7.559 1.58e-12 ***
tt 0.44312 0.05861 7.561 1.56e-12 ***
z.diff.lag 0.04937 0.07153 0.690 0.491 この回帰結果には、(Intercept)とttの両方が含まれています。
-
z.lag.1: 単位根の有無を判断するための項です。係数γの推定値は-0.55479と負で、統計的にも有意です。この係数に対するt値-7.559が、単位根検定の検定統計量になります。 -
tt: 時間トレンドの係数です。0.44312という推定値は、この時系列が平均して1期間あたり約0.44ずつ上昇するトレンドを持つことを示唆しています。こちらも統計的に有意であり、トレンド項をモデルに含めたことが適切であったことを示しています。
検定統計量と棄却限界値の比較
Value of test-statistic is: -7.5586 70.0758 28.5859
Critical values for test statistics:
1pct 5pct 10pct
tau3 -3.99 -3.43 -3.13
phi2 6.22 4.75 4.07
phi3 8.43 6.49 5.47type="trend"の場合、検定統計量と棄却限界値が3種類出力されます。
- tau3統計量(単位根の検定)
-
Value of test-statistic is: -7.5586: 1つ目の値がtau3統計量です。これは回帰モデルのz.lag.1のt値(-7.559)と同じものであり、単位根の存在(γ=0)を検定するためのものです。
-
- phi2統計量(単位根とトレンドの同時検定)
-
Value of test-statistic is: 70.0758: 2つ目の値がphi2統計量です。「トレンド項は0であり、かつ、単位根が存在する(β=0, γ=0)」という同時仮説を検定します。
-
- phi3統計量(単位根とドリフトとトレンドの同時検定)
-
Value of test-statistic is: 28.5859: 3つ目の値がphi3統計量です。「定数項もトレンド項も0であり、かつ、単位根が存在する(α=0, β=0, γ=0)」という最も制約の強い同時仮説を検定します。これはモデル全体の適合度を評価するF検定に似た役割を持ちます。
-
結論の導出
最初に、主目的である単位根の有無をtau3統計量で判断します。
- 帰無仮説 (H₀): 単位根が存在する。
- 判断ルール:
検定統計量(tau3) < 棄却限界値(tau3)であれば、帰無仮説を棄却する。
有意水準5%で判断します。
- 検定統計量 (tau3):
-7.5586 - 5%棄却限界値 (tau3):
-3.43
-7.5586 < -3.43ですので、検定統計量は棄却限界値を下回っています。
ですので、帰無仮説「単位根が存在する」は棄却されます。 この結果は、このデータが非定常な単位根過程ではないことを強く示唆しています。
次に、phi2およびphi3でモデルの妥当性を確認します。
phi3統計量を見てみましょう。
- 帰無仮説 (H₀): 定数項もトレンド項も不要であり、かつ単位根が存在する。
- 検定統計量 (phi3):
28.5859 - 5%棄却限界値 (phi3):
6.49
28.5859 > 6.49ですので、帰無仮説は棄却されます。この結果は、モデルに定数項やトレンド項を含めることが適切であったことを示しています。
総合的な結論: 単位根の存在を検定するtau3統計量の結果、帰無仮説が棄却されました。加えて、回帰モデルのトレンド項ttが統計的に有意であり、モデルの妥当性を検定するphi3統計量も有意でした。
これらの結果を総合すると、この時系列データは「単位根を持たず、確定的な時間トレンドの周りで変動する、トレンド定常過程である」と結論付けられます。こちらもデータ生成時の設定と完全に一致する、正しい検定結果です。
以上です。