Rの関数:ur.ers {urca}

Rの関数から ur.ers {urca} を確認します。

本ポストはこちらの続きです。

Rの関数:ur.kpss {urca}
Rの関数から ur.kpss {urca} を確認します。本ポストはこちらの続きです。ur.kpss関数についてur.kpss関数は、tseriesパッケージのkpss.testと同様に、クウィアトコウスキー–フィリップス–シュミット–シン...
www.saecanet.com
2025.10.14

ur.ers関数について

ur.ersは、エリオット–ローゼンバーグ–ストック（Elliot, Rothenberg, and Stock, ERS）検定 を実行するための関数です。

ADF検定との主な違いと特徴

  1. データの前処理: ADF検定では、トレンドを持つデータに対して、通常の最小二乗法（OLS）を用いてトレンドを除去（detrending）しますが、ERS検定は、一般化最小二乗法（Generalized Least Squares, GLS） を用いてデータのトレンドを除去します。
  2. 検出力: GLSによる前処理の結果、ERS検定は自己回帰係数が1に近い（しかし1ではない）定常過程、つまり持続性の高い（highly persistent）定常過程を、非定常な単位根過程と区別する能力がADF検定よりも向上しています。

検定の帰無仮説はADF検定と同じく「単位根が存在する（時系列は非定常である）」です。

ur.ers関数の引数について

library(urca)
args(ur.ers)
function (y, type = c("DF-GLS", "P-test"), model = c("constant", 
    "trend"), lag.max = 4) 
NULL

y

検定の対象となる時系列データを指定します。

type

実行するERS検定の種類を指定します。

  • "DF-GLS"（デフォルト）: GLSによってトレンド除去されたデータに対して、ディッキー–フラー形式の検定を実行します。
  • "P-test": ERSの論文で提案されているもう一つの検定で、point-optimal testと呼ばれます。DF-GLS検定とは異なる検定統計量を計算します。

model

検定の対立仮説となる定常性の種類を指定し、GLSによるトレンド除去の方法を決定します。

  • "constant"（デフォルト）: 対立仮説をStationarity round a constant levelとします(本ポストでは以降「水準定常性」と呼称)。データから定数項（平均値）をGLSで除去した上で検定を行います。
  • "trend": 対立仮説をStationarity around a deterministic trendとします(本ポストでは以降「トレンド定常性」と呼称)。データから時間トレンドをGLSで除去した上で検定を行います。

lag.max

DF-GLS検定の回帰式に含めるラグ次数を決定する際に、考慮する最大のラグ数を指定します。関数は1からlag.maxまでの範囲で最適なラグ次数を情報量規準などに基づいて自動的に選択します。

シミュレーション

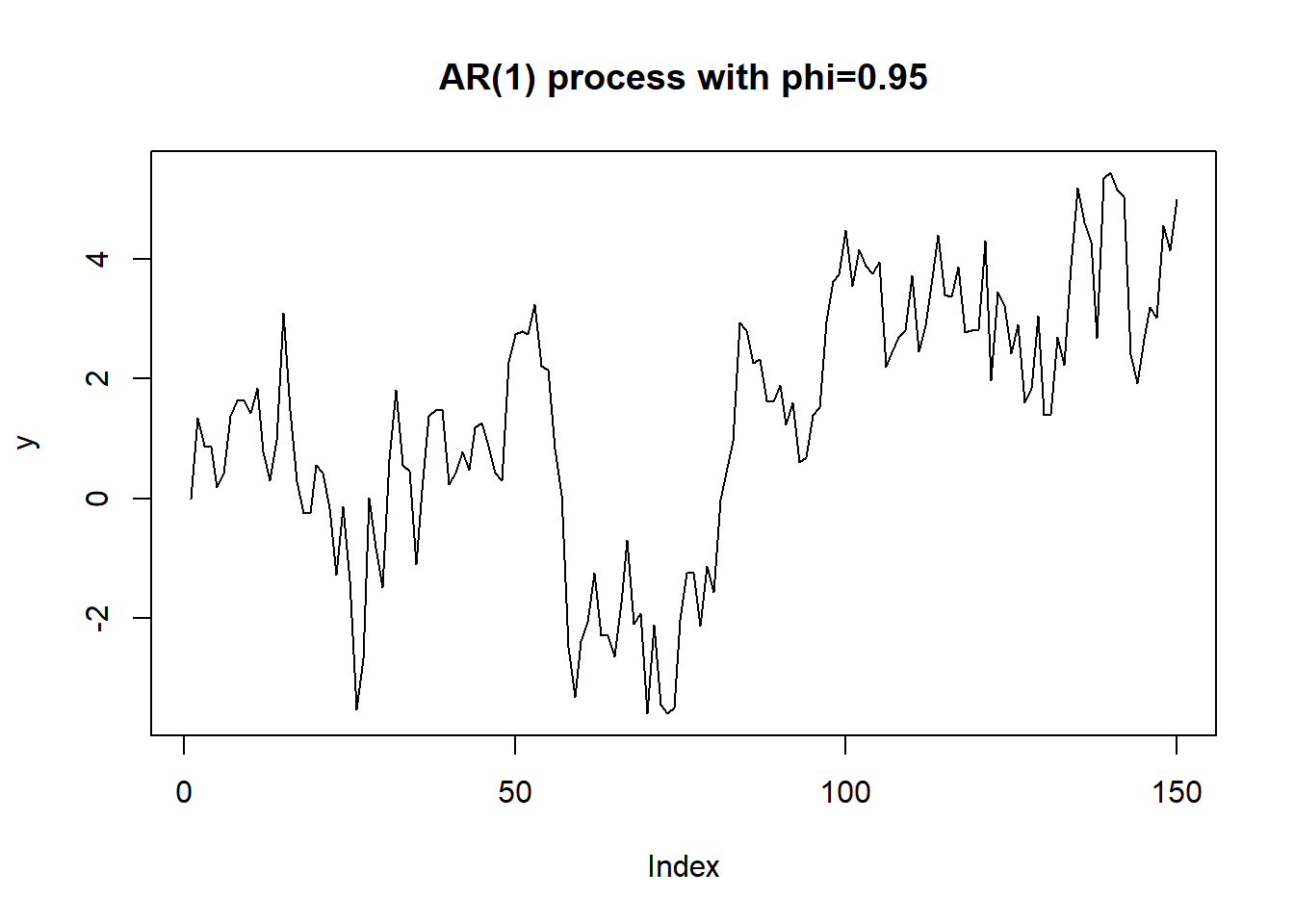
ERS検定の検出力を確認するために、定常過程(phi = 0.95)のサンプル時系列データを生成し、通常のADF検定(ur.df)とERS検定(ur.ers)の結果を比較します。

# 再現性を確保するために乱数のシードを設定します
seed <- 20251015
set.seed(seed)

# 定常過程（AR(1) with phi=0.95）のサンプル時系列データを生成
n <- 150
phi <- 0.95
e <- rnorm(n)
y <- numeric(n)
for (t in 2:n) y[t] <- phi * y[t - 1] + e[t]

plot(y, type = "l", main = "AR(1) process with phi=0.95")
Figure 1

始めに、通常のADF検定を実行します。

# Augmented Dickey-Fuller test
adf_result <- ur.df(y, type = "trend", lags = 1)
summary(adf_result)

############################################### 
# Augmented Dickey-Fuller Test Unit Root Test # 
############################################### 

Test regression trend 


Call:
lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.68378 -0.63069  0.07194  0.58093  2.45392 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) -0.173662   0.166797  -1.041  0.29955   
z.lag.1     -0.146393   0.045885  -3.190  0.00174 **
tt           0.005124   0.002262   2.265  0.02498 * 
z.diff.lag  -0.051607   0.082806  -0.623  0.53412   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9735 on 144 degrees of freedom
Multiple R-squared:  0.08246,   Adjusted R-squared:  0.06334 
F-statistic: 4.314 on 3 and 144 DF,  p-value: 0.006033


Value of test-statistic is: -3.1904 3.545 5.2558 

Critical values for test statistics: 
      1pct  5pct 10pct
tau3 -3.99 -3.43 -3.13
phi2  6.22  4.75  4.07
phi3  8.43  6.49  5.47

1. 検定の仮説

  • 帰無仮説 (H₀): データ y には単位根が存在する（データは非定常である）。
  • 対立仮説 (H₁): データ y には単位根が存在しない（データは定常、またはトレンド周りに定常である）。

2. 検定結果の確認

  • 検定統計量 (Value of test-statistic): -3.1904
  • 臨界値 (Critical values for test statistics):

    • 1%水準 (1pct): -3.99
    • 5%水準 (5pct): -3.43
    • 10%水準 (10pct): -3.13

今回の検定は type = "trend" で実行されており、データに時間トレンドが存在することを想定したモデルです。そのため、対応する臨界値は tau3 の行を参照します。

3. 結論

検定統計量 -3.1904 は、有意水準5%の臨界値 -3.43 よりも大きいため、元のデータは phi=0.95 の定常過程として生成されていますが、帰無仮説「データは非定常である」を棄却することはできません。

続いて、ERS検定を実行します。

# DF-GLS (Elliott-Rothenberg-Stock) test
ers_result <- ur.ers(y, type = "DF-GLS", model = "trend", lag.max = 1)
summary(ers_result)

############################################### 
# Elliot, Rothenberg and Stock Unit Root Test # 
############################################### 

Test of type DF-GLS 
detrending of series with intercept and trend 


Call:
lm(formula = dfgls.form, data = data.dfgls)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.75189 -0.66642  0.02734  0.52434  2.49927 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
yd.lag       -0.13941    0.04488  -3.106  0.00228 **
yd.diff.lag1 -0.05407    0.08239  -0.656  0.51268   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9699 on 146 degrees of freedom
Multiple R-squared:  0.07651,   Adjusted R-squared:  0.06386 
F-statistic: 6.048 on 2 and 146 DF,  p-value: 0.002996


Value of test-statistic is: -3.1062 

Critical values of DF-GLS are:
                 1pct  5pct 10pct
critical values -3.46 -2.93 -2.64

1. 検定の仮説

  • 帰無仮説 (H₀): データ y には単位根が存在する（データは非定常である）。
  • 対立仮説 (H₁): データ y には単位根が存在しない（データはトレンド周りに定常である）。

2. 検定結果の確認

  • 検定統計量 (Value of test-statistic): -3.1062
  • 臨界値 (Critical values of DF-GLS):

    • 1%水準 (1pct): -3.46
    • 5%水準 (5pct): -2.93
    • 10%水準 (10pct): -2.64

3. 結論

検定統計量 -3.1062 は、有意水準5%の臨界値 -2.93 よりも小さいため、帰無仮説「データは非定常である」は棄却されます。

サンプル時系列データは定常過程として生成していますので、データと検定結果は整合しています。

以上です。