Rの関数:nls {stats}

Rの関数から nls {stats} を確認します。

`nls`関数とは

nls（Nonlinear Least Squares）関数は、観測データを非線形モデルに当てはめるための関数です。

線形回帰が応答変数と説明変数の間の線形関係を仮定するのに対し、非線形回帰はより複雑な関係性を表現するモデルのパラメータを、最小二乗法を用いて推定します。

具体的には、モデルの予測値と実際の観測値の差（残差）の二乗和を最小化するようなパラメータの値を、反復計算によって探索します。

`nls`関数の引数

nls関数の主要な引数は以下のとおりです。

formula:
- モデルの構造を定義する式です。response ~ predictor_expression の形式で記述します。predictor_expression は、説明変数と推定したいパラメータ（例: a, b）を含む数式となります。チルダ(~)の左側に応答変数、右側にパラメータを含む非線形モデル式を記述します。
data:
- モデル式に含まれる変数が格納されたデータフレームまたはリストを指定します。このデータソースから、formulaで指定された変数が検索されます。
start:
- パラメータの初期値を指定する、名前付きのリストまたはベクトルです。非線形モデルのパラメータ推定は反復計算で行われるため、計算を開始するための初期値が不可欠です。適切な初期値を設定することが、収束の成功率を高める上で重要となります。
control:
- アルゴリズムの挙動を制御するためのパラメータを設定します。nls.control()関数を用いて、最大反復回数（maxiter）、収束判定の閾値（tol）などをリスト形式で指定できます。
algorithm:
- パラメータ推定に使用するアルゴリズムを指定します。主要な選択肢は以下の通りです。
- "default": デフォルトのアルゴリズム（Gauss-Newton法）を使用します。
- "plinear": モデルの一部がパラメータに対して線形である場合に使用するplinearアルゴリズム（partially linear model）です。
- "port": PORTライブラリの nl2sol アルゴリズムを使用します。このアルゴリズムは、パラメータに制約（上限・下限）を設けたい場合に有用です。
trace:
- 論理値（TRUEまたはFALSE）で指定します。TRUEに設定すると、反復計算の過程（パラメータ値や残差平方和の変化）が出力されます。これは、アルゴリズムがどのように収束に向かっているか、あるいはなぜ収束しないのかをデバッグする際に役立ちます。
subset:
- dataの中から、モデルの当てはめに使用するデータのサブセットを指定するためのベクトルです。
weights:
- 各観測値に対する重みを指定します。例えば、測定の精度が観測ごとに異なる場合、精度の高い観測値の重みを大きくするといった調整が可能です。
na.action:
- データに欠損値（NA）が含まれている場合の処理方法を指定します。
model:
- 論理値で指定します。TRUEに設定すると、返されるオブジェクトにモデルフレームが含まれるようになります。
lower, upper:
- パラメータが取りうる値の下限と上限を指定します。これらの引数は algorithm = "port" を選択した場合にのみ有効です。パラメータの探索範囲を物理的制約などに基づいて限定したい場合に使用します。

シミュレーション

nls関数を確認するため、指数関数的な成長にノイズが加わったデータを想定したシミュレーションを行います。

なお、有意水準は5%とします。

1. サンプルデータの作成と可視化

始めに、モデル y = a * exp(b * x) に従って生成されるデータに、正規分布する誤差を加えたサンプルデータを作成します。パラメータの真の値は a = 5、b = 0.3 と設定します。

# 乱数のシードを固定し、再現性を確保
seed <- 20251109
set.seed(seed)

# パラメータの真の値を設定
a_true <- 5
b_true <- 0.3

# 独立変数 x を生成
x <- seq(0, 10, length.out = 50)

# 真のモデルに従う y の値を計算し、ノイズを加える
y_true <- a_true * exp(b_true * x)
y_obs <- y_true + rnorm(length(x), mean = 0, sd = 10)

# データフレームを作成
sample_data <- data.frame(x = x, y = y_obs)

# データをプロットして関係性を視覚的に確認
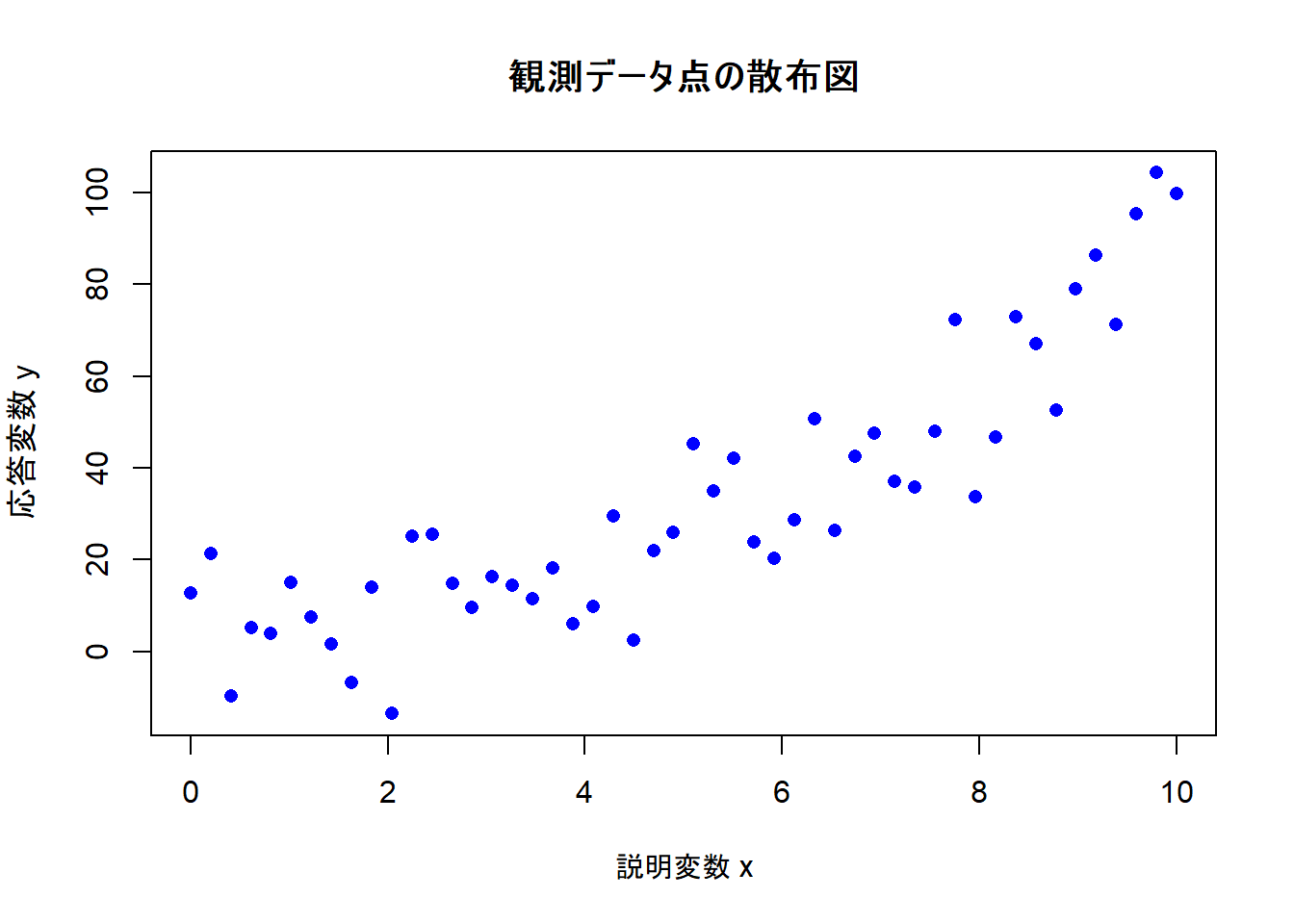
plot(sample_data$x, sample_data$y,
  main = "観測データ点の散布図",
  xlab = "説明変数 x",
  ylab = "応答変数 y",
  pch = 16, col = "blue"
)

2. `nls`によるモデルフィッティング

作成したサンプルデータに対して、nls関数を用いて非線形モデルを当てはめます。パラメータaとbの初期値を設定し、モデルのフィッティングを実行します。

# パラメータの初期値を設定
# 散布図から、x=0 のとき y は 12 付近であることから a の初期値を 12 と推測
# x が増加すると y も増加するため、b は正の値と推測し、0.1 と設定
start_values <- list(a = 12, b = 0.1)

# nls関数による非線形回帰の実行
# formula にはモデル式 y ~ a * exp(b * x) を指定
# data には作成したデータフレームを、start には初期値を渡す
cat("--- 収束過程 ---\n")
nls_model <- nls(y ~ a * exp(b * x),
  data = sample_data,
  start = start_values,
  trace = TRUE
) # trace=TRUEで計算過程を表示

--- 収束過程 ---
34689.30    (2.04e+00): par = (12 0.1)
15311.61    (1.27e+00): par = (5.653967 0.2405088)
6652.815    (3.65e-01): par = (5.037875 0.31043)
5870.572    (1.26e-02): par = (5.317549 0.2942412)
5869.633    (2.15e-04): par = (5.365787 0.2928848)
5869.633    (2.99e-06): par = (5.367142 0.2928591)

trace = TRUE を指定したことで、反復計算の過程で残差平方和が減少していく様子が確認できます。

# フィッティング結果の要約を表示
cat("--- nlsモデルの要約 ---\n")
print(summary(nls_model))

--- nlsモデルの要約 ---

Formula: y ~ a * exp(b * x)

Parameters:
  Estimate Std. Error t value Pr(>|t|)    
a  5.36714    1.04756   5.123 5.29e-06 ***
b  0.29286    0.02276  12.865  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 11.06 on 48 degrees of freedom

Number of iterations to convergence: 5 
Achieved convergence tolerance: 2.993e-06

`nls`モデルの要約結果の確認

Formula: y ~ a * exp(b * x)

これは、nls関数に与えられたモデルの式を示しています。応答変数 y が、説明変数 x と2つのパラメータ a および b によって構成される指数関数 a * exp(b * x) に従って変動すると仮定しています。

Parameters:

このセクションでは、推定された各パラメータに関する情報が提供されます。

	Estimate	Std. Error	t value	Pr(>	t
a	5.36714	1.04756	5.123	5.29e-06	***
b	0.29286	0.02276	12.865	< 2e-16	***

Estimate (推定値):
- 残差平方和を最小化することによって得られたパラメータの最適値です。パラメータ a の推定値は約 5.37、b の推定値は約 0.29 です。シミュレーションで設定した真の値（a=5, b=0.3）に近い値が推定されており、モデルがデータを捉えていることが示唆されます。
Std. Error (標準誤差):
- パラメータ推定値のばらつき、すなわち推定の精度を示す指標です。この値が小さいほど、推定値の信頼性が高いと解釈できます。
t value (t値):
- 各パラメータが 0 と有意に異なるかどうかを検定するための統計量です。Estimate / Std. Error によって計算されます。この絶対値が大きいほど、パラメータがモデルに対して重要であることを意味します。
Pr(>|t|) (p値):
- パラメータの係数が実際には 0 であるという帰無仮説のもとで、観測されたt値以上の値が得られる確率を示します。この確率が設定した有意水準より小さい場合、帰無仮説は棄却され、パラメータは統計的に有意であると判断されます。
- a と b のp値は、それぞれ 5.29e-06 と < 2e-16 であり、どちらも設定した有意水準を下回っています。それゆえ、両方のパラメータがモデルに対して統計的に有意であることが支持されます。Signif. codes の *** は、p値が 0.001 未満であることを示す記号です。

Residual standard error: 11.06 on 48 degrees of freedom

Residual standard error (残差標準誤差):
- モデルの予測値が実際の観測値から平均してどの程度ずれているかを示す指標です。これは、モデルの当てはまりの良さを表し、値が小さいほどモデルがデータをよく説明していることを意味します。このモデルでは、当てはめによる誤差の平均的な大きさが約 11.06 であることを示しています。
degrees of freedom (自由度):
- 残差の自由度は、「観測数 – パラメータ数」で計算されます（この場合、50 – 2 = 48）。

Number of iterations to convergence: 5

モデルのパラメータを最適化するために、アルゴリズムが5回の反復計算を行ったことを示しています。少ない回数で収束していることは、アルゴリズムが効率的に最適解を見つけられたことを意味します。

Achieved convergence tolerance: 2.993e-06

収束判定の閾値（tolerance）に到達したことを示しています。この値は、反復計算の最終ステップにおけるパラメータの変化量が小さくなり、計算が収束したと判断されたことを示すものです。

3. 結果の可視化

最後に、元の散布図に、nlsによって推定されたパラメータを用いたモデル曲線を重ねて描画します。これにより、モデルがどの程度データに適合しているかを視覚的に評価できます。

# 元のデータの散布図を再度描画
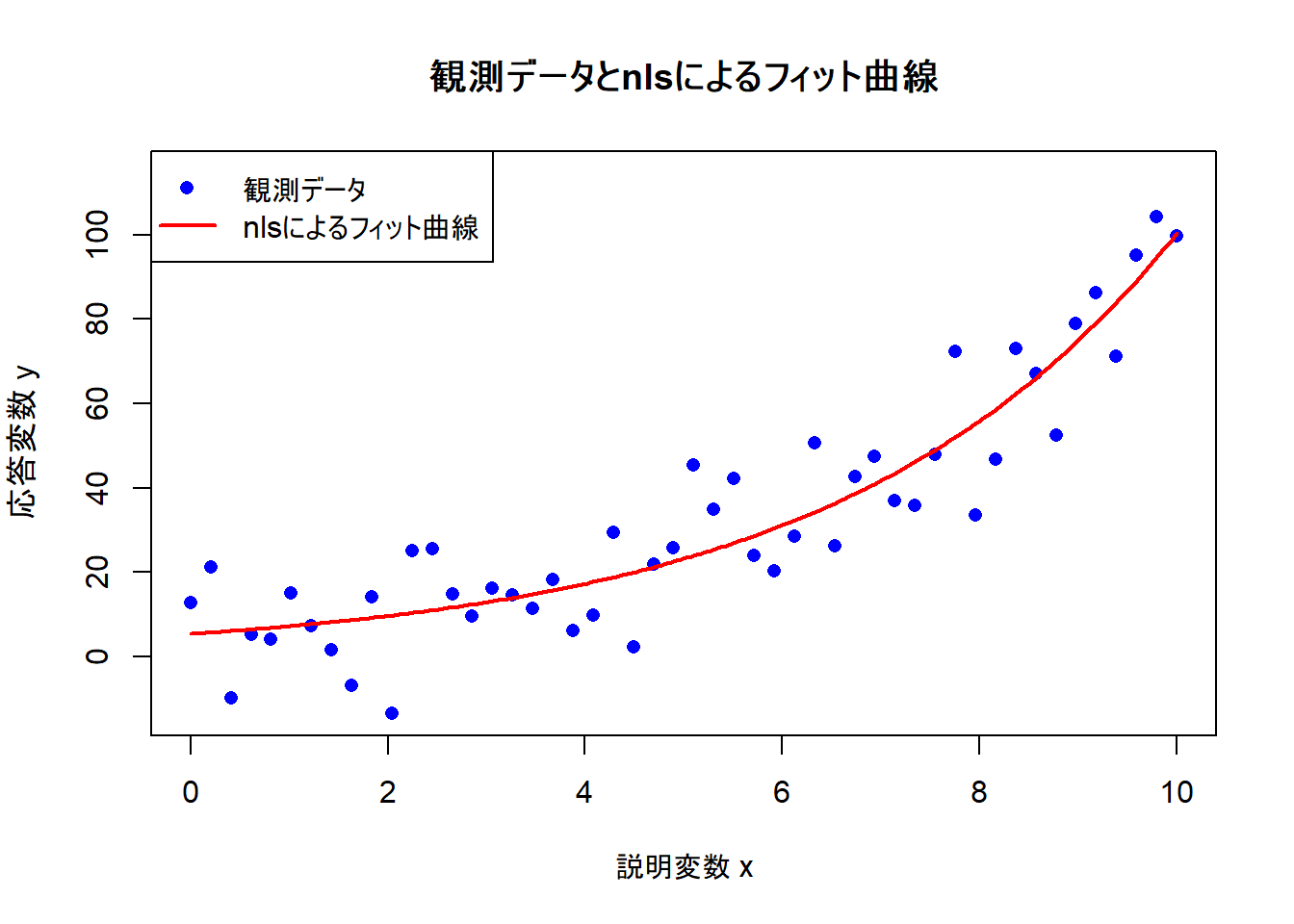
plot(sample_data$x, sample_data$y,
  main = "観測データとnlsによるフィット曲線",
  xlab = "説明変数 x",
  ylab = "応答変数 y",
  pch = 16, col = "blue",
  ylim = c(min(y_obs), max(y_obs) * 1.1)
) # y軸の範囲を調整

# 推定されたパラメータを取得
params <- coef(nls_model)
a_est <- params["a"]
b_est <- params["b"]

# フィットした曲線を描画するための x の値を生成
x_curve <- seq(min(x), max(x), length.out = 200)

# 推定されたパラメータを用いて y の値を計算
y_curve <- a_est * exp(b_est * x_curve)

# 散布図にフィットした曲線を追加
lines(x_curve, y_curve, col = "red", lwd = 2)

# 凡例を追加
legend("topleft",
  legend = c("観測データ", "nlsによるフィット曲線"),
  col = c("blue", "red"),
  pch = c(16, NA),
  lty = c(NA, 1),
  lwd = c(NA, 2)
)