Rの関数から s {mgcv} を確認します。
本ポストは、こちらの続きです。

s関数とは
mgcv::s関数は、gamのモデル式内において、変数の平滑化項を定義するための関数です。
本関数自体がデータを平滑化するわけではなく、その役割は、gam関数に対して、指定された変数をどのように平滑化すべきか、その「仕様」を伝えることにあります。
s()関数は、平滑化に使用する基底関数の種類(例:スプライン)、基底の次元(複雑さの上限)、罰則(ペナルティ)の形式などを引数で指定することで、柔軟なモデル構築を可能にします。
gam関数は、s()によって生成された仕様オブジェクトを解釈し、モデルフィッティングに必要な計画行列と罰則行列を内部で構築します。
s関数の主要な引数
library(mgcv)
args(s)function (..., k = -1, fx = FALSE, bs = "tp", m = NA, by = NA,
xt = NULL, id = NULL, sp = NULL, pc = NULL)
NULL...:平滑化の対象となる1つ以上の変数(共変量)を指定します。
s(x)のように1次元のスムーズを定義したり、s(x, z)のように多次元のスムーズを定義したりできます。k:平滑化に使用する基底関数の次元(数)を指定する整数値です。この値は、平滑化項が取りうる複雑さの上限を定めます。
kを大きくすると、より複雑で波打った関数を表現できますが、過剰適合のリスクも増大します。k=-1(デフォルト)の場合、mgcvがデータに応じて適切な値を自動的に選択します。有効自由度(edf)は、このkの値を超えることはありません。fx:TRUEに設定すると、この項は罰則化されない(fixed)回帰スプラインとして扱われます。その場合、自由度はk-1に固定されます。FALSE(デフォルト)の場合は、平滑化パラメータを用いて罰則化が行われ、有効自由度はデータから推定されます。bs:平滑化に使用する基底関数の種類(basis type)を指定する文字列です。代表的なものには以下があります。
-
"tp"(Thin Plate Regression Splines): デフォルト。低次元のスムーズに適しており、基底次元kの選択に比較的頑健です。 -
"cr"(Cubic Regression Splines): 1次元のスムーズに適した3次スプラインです。 -
"ps"(P-splines): B-spline基底と差分ペナルティを組み合わせたものです。 -
"cc"(Cyclic Cubic Splines): 周期性を持つデータ(例:時刻、月)に適した3次スプラインです。
-
m:罰則(ペナルティ)の次数を指定します。例えば3次スプライン(
bs="cr")の場合、m=2(デフォルト)は関数の2階微分(曲率)に対して罰則を科し、滑らかな曲線を促します。m=1とすると1階微分(傾き)に罰則を科します。by:変数によって平滑化曲線の形状を変化させる「Varying Coefficient Model(変動係数モデル)」を定義します。
byに指定された変数の値に応じて、s()で指定された変数の効果が変化します。by変数が数値の場合はその値に比例して、因子(factor)の場合はその水準ごとに異なる平滑化曲線が推定されます。xt:平滑化基底の種類によっては、追加の制御情報(例えば、使用するB-splineの次数など)をリスト形式で渡すことができます。
id:複数の平滑化項に同じ平滑化パラメータを使用させたい場合に、共通のID番号を振るために使用します。
sp:この平滑化項に対する平滑化パラメータの値を直接指定します。通常は
gam関数が自動推定します。pc:特定の点における平滑化関数の値を0に制約する場合などに使用する引数です。
シミュレーションによるs関数の確認
s()関数の主要な引数であるkとbyが、モデルの推定結果にどのような影響を与えるかをシミュレーションで確認します。
なお、有意水準は5%とします。
サンプルデータの作成
応答変数yと説明変数xの間に非線形の関係が存在し、さらにその関係が2つのグループ(A, B)で異なるような状況を想定したデータを作成します。
- グループA:
yはxのsin関数に従う。 - グループB:
yはxのcos関数に従う(Aとは形状が異なる)。
# 再現性のための乱数シード固定
seed <- 20251114
set.seed(seed)
n <- 200 # 各グループのデータ点数
# グループAのデータを作成
x_a <- seq(0, 2 * pi, length.out = n)
true_f_a <- 2 * sin(x_a)
y_a <- true_f_a + rnorm(n, mean = 0, sd = 0.8)
# グループBのデータを作成
x_b <- seq(0, 2 * pi, length.out = n)
true_f_b <- -1.5 * cos(x_b) + 1 # Aとは異なる形状と切片
y_b <- true_f_b + rnorm(n, mean = 0, sd = 0.8)
# データを一つのデータフレームに結合
sample_data_s <- data.frame(
y = c(y_a, y_b),
x = c(x_a, x_b),
group = factor(rep(c("A", "B"), each = n))
)
# 生成したデータの一部を確認
cat("--- 生成されたサンプルデータの一部を確認 ---\n")
print(str(sample_data_s))--- 生成されたサンプルデータの一部を確認 ---
'data.frame': 400 obs. of 3 variables:
$ y : num 0.0925 -0.4881 1.2092 -0.552 1.0411 ...
$ x : num 0 0.0316 0.0631 0.0947 0.1263 ...
$ group: Factor w/ 2 levels "A","B": 1 1 1 1 1 1 1 1 1 1 ...
NULL1. 基本的な平滑化 s(x)
まず、グループの違いを無視して、xに対する基本的な平滑化項をモデル化します。
cat("--- モデル1: グループを無視した基本的な平滑化 ---\n")
# グループを考慮せずにモデルをフィッティング
gam_mod1 <- gam(y ~ s(x), data = sample_data_s)
print(summary(gam_mod1))
# 結果のプロット
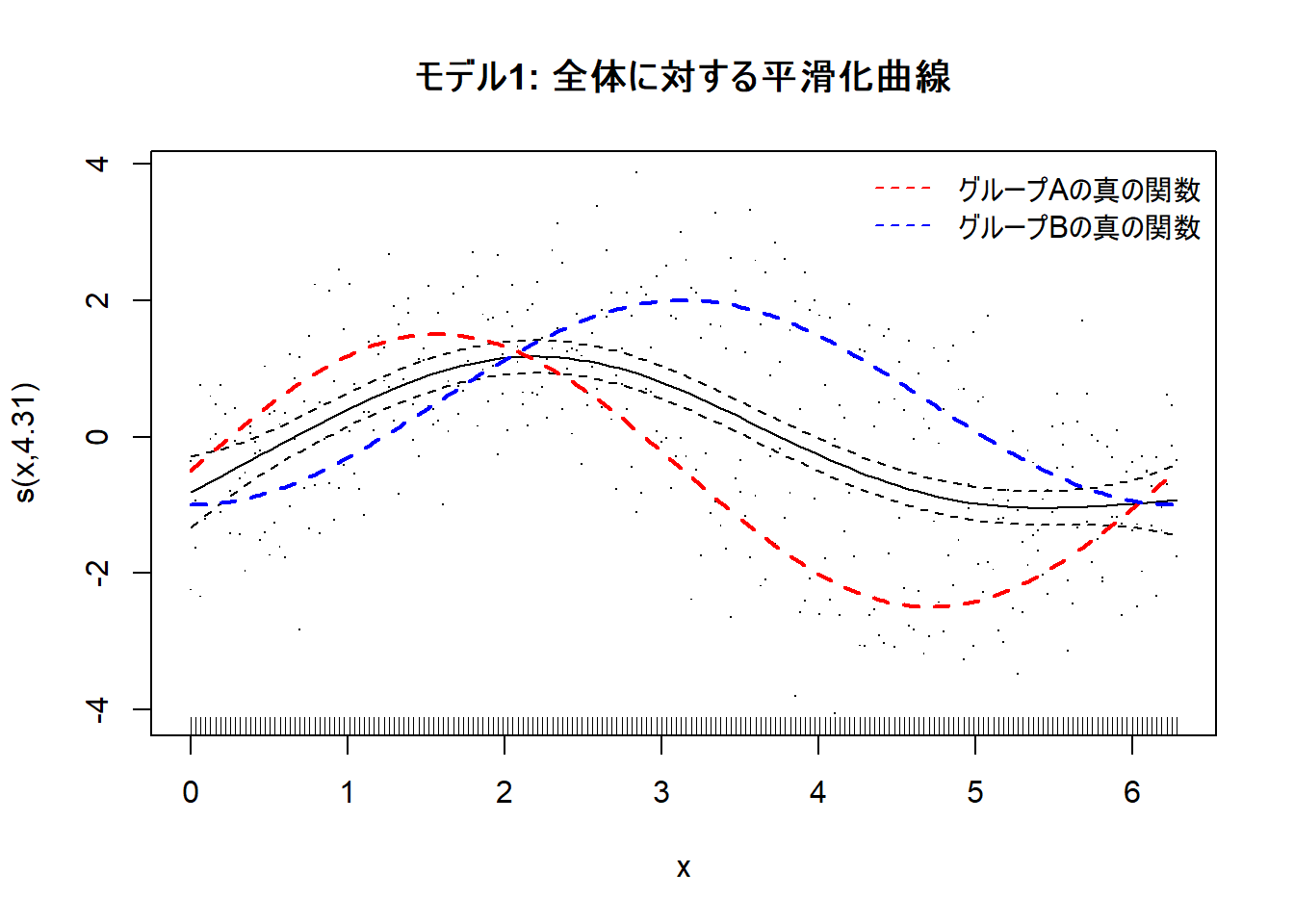
plot(gam_mod1, residuals = TRUE, shade = TRUE, main = "モデル1: 全体に対する平滑化曲線")
# グループごとの真の関数を重ね描き
lines(x_a, true_f_a - mean(c(true_f_a, true_f_b)), col = "red", lty = 2, lwd = 2)
lines(x_b, true_f_b - mean(c(true_f_a, true_f_b)), col = "blue", lty = 2, lwd = 2)
legend("topright",
legend = c("グループAの真の関数", "グループBの真の関数"),
col = c("red", "blue"), lty = 2, bty = "n"
)--- モデル1: グループを無視した基本的な平滑化 ---
Family: gaussian
Link function: identity
Formula:
y ~ s(x)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.44772 0.06567 6.817 3.49e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(x) 4.305 5.3 29.94 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.289 Deviance explained = 29.6%
GCV = 1.7484 Scale est. = 1.7252 n = 400Family: gaussian / Link function: identity
- モデルが応答変数
yの誤差構造として正規分布(ガウス分布)を、リンク関数として恒等関数(identity)を仮定していることを示します。今回のシミュレーションデータは正規分布に従う誤差を加えて生成したため、この設定は適切です。
Formula: y ~ s(x)
- モデルの構造式です。応答変数
yを、説明変数xの単一の平滑化項s(x)によって説明しようとしていることを意味します。このモデル式にはgroup変数が含まれていません。それゆえ、モデルはグループAとグループBの区別なく、全てのデータに対して一本の平滑化曲線を当てはめようとします。
Parametric coefficients:
- モデルに含まれる線形項(パラメトリックな項)の係数です。このモデルでは切片
(Intercept)のみです。 - Estimate: 切片の推定値は
0.44772です。 - Pr(>|t|): p値は
3.49e-11と設定した有意水準を下回っており、この切片が統計的に有意であることを示しています。
Approximate significance of smooth terms:
- 平滑化項
s(x)の評価を示す部分です。 - edf (有効自由度):
4.305という値になっています。1より大きいこの値は、モデルがxとyの間に明確な非線形関係を検出したことを示唆しています。ただし、この非線形性はグループAのsin波とグループBのcos波という、本来異なる2つのパターンを無理に一つの曲線で表現しようとした結果、両者の中間的な形状を捉えようとしたことによるものです。 - F / p-value: F統計量の値が
29.94と大きく、p値が<2e-16と有意水準を下回っていることから、平滑化項s(x)は統計的に有意であると判断されます。すなわち、xがyを予測する上で有意な説明変数であることになります。
モデル全体の適合度
- R-sq.(adj) = 0.289: 調整済み決定係数が
0.289、つまり約28.9%であることを示しています。モデルがデータ全体のばらつきの3割弱しか説明できていないことを意味し、適合度はあまり高くないと言えます。 - Deviance explained = 29.6%: 逸脱度の説明率も同様に約29.6%であり、低い値です。
- GCV = 1.7484: 一般化交差検証(Generalized Cross-Validation)スコアです。モデル選択の際の一つの指標となります。
総括
- 有意な非線形関係の検出: モデルは、
xとyの間に単純な直線ではない、有意な非線形関係が存在すること自体は捉えています(edf > 1,p-value < 0.001)。 - モデルの本質的な限界: しかし、データが持つ「グループごとに
xとyの関係性が異なる」という構造を無視しているため、モデル全体の適合度は低くなっています(R-sq.(adj) = 0.289)。Figure 1 の通り、単一の曲線では、sin波とcos波という2つの異なるパターンを同時にうまく表現することはできず、その結果として多くの情報(データのばらつき)が残差として説明できないまま残ってしまっています。
この結果は、「統計的に有意な項がある」ことと「モデルとして適切である」ことは必ずしも同義ではないことを示しています。そして、s()関数のby引数を用いてグループ構造をモデルに組み込むことの重要性を示唆しています。
2. k引数による複雑さの制限
次に、k引数を用いて、意図的にモデルの複雑さを制限してみます。k=3と設定すると、平滑化項は最大でも2次の多項式程度の単純な曲線しか表現できなくなります。
cat("--- モデル2: k=3で複雑さを制限した平滑化 ---\n")
# k=3 を指定してフィッティング
gam_mod2 <- gam(y ~ s(x, k = 3), data = sample_data_s)
print(summary(gam_mod2))
# 結果のプロット
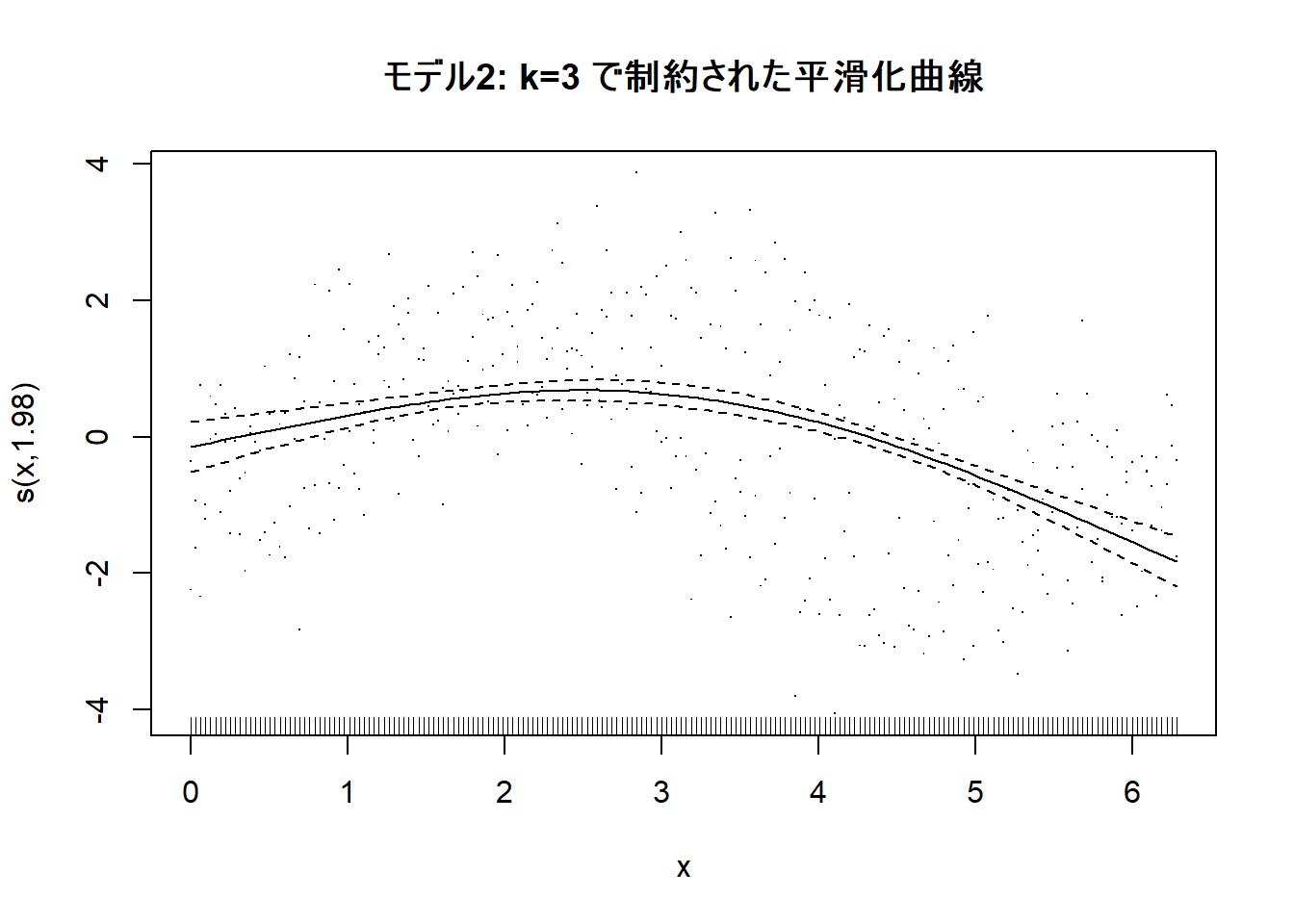
plot(gam_mod2, residuals = TRUE, shade = TRUE, main = "モデル2: k=3 で制約された平滑化曲線")--- モデル2: k=3で複雑さを制限した平滑化 ---
Family: gaussian
Link function: identity
Formula:
y ~ s(x, k = 3)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.44772 0.06964 6.429 3.68e-10 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(x) 1.981 2 51.13 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.2 Deviance explained = 20.4%
GCV = 1.9543 Scale est. = 1.9397 n = 400Formula: y ~ s(x, k = 3)
- このモデルの特徴は、式内の
s(x, k = 3)という部分です。k = 3と指定することにより、gam関数に対して「xの平滑化項を表現するために使用できる基底関数の数を3つに制限せよ」と指定しています。 - 基底関数の数が3つである場合、モデルが表現できる関数の形状は、最大でも2次関数(放物線)程度にまで単純化されます。データの持つ複雑なsin波やcos波の形状を捉えるには、不十分な設定です。
Approximate significance of smooth terms:
- 平滑化項
s(x)の評価を示します。このセクションから、k=3という制約がモデルに与えた影響を明確に読み取ることができます。 - edf (有効自由度):
1.981となっています。この値は、指定された上限であるk-1 = 2に近い値です。これは、モデルがデータにより良くフィットしようと、与えられた柔軟性(自由度)を上限いっぱいまで使い切っている状態を示唆しています。この現象は、kの値が小さすぎる可能性を示す警告サインです。モデルはもっと複雑になりたいのに、kによってその能力が抑制されているのです。 - F / p-value:
p値は<2e-16と依然として有意水準を下回っており、この単純化された曲線でさえも、xがyを説明する上で統計的に有意な項であることを示しています。しかしながら、これは「全く関係がない(平坦な線)」という帰無仮説と比較して有意であるに過ぎず、モデルがデータを適切に表現できていることを意味するものではありません。
モデル全体の適合度
- R-sq.(adj) = 0.200: 調整済み決定係数は
0.200(20.0%)です。kを制限しなかったgam_mod1の0.289から低下しており、モデルがデータのばらつきを説明する能力がさらに失われたことを示しています。 - Deviance explained = 20.4%: 逸脱度の説明率も同様に20.4%と低い値です。
- GCV = 1.9543: 一般化交差検証スコアは
1.9543であり、gam_mod1の1.7484よりも悪化しています。GCVスコアは値が小さいほど良いモデル(予測性能が高い)とされるため、このモデルの予測性能が低いことが示唆されます。
総括
gam_mod2のサマリーは、s()関数のk引数の重要性を示す実例です。
- 不適切な
kの選択:k=3という小さすぎる値を設定したため、モデルはデータの背後にある真の関数形(sin波とcos波の混合)を全く捉えることができず、Figure 2 の通り、単純な放物線状の近似しかできませんでした。 - 診断的価値:
edfがk-1に近い値を取ったことは、「kの値がモデルの表現力を不当に制限している」という診断情報を提供します。実世界のデータ分析においてこのような状況に遭遇した場合、kの値をより大きく設定してモデルを再評価する必要があります。
結論として、このモデルはkという制約によってデータの構造を正しく学習できず、結果として適合度の低い、不適切なモデルとなりました。
3. by引数によるグループ別の平滑化
最後に、by引数を用いて、グループごとに異なる平滑化曲線を推定します。by引数には因子型変数groupを指定します。
cat("--- モデル3: by=group でグループ別に平滑化 ---\n")
# by引数を用いてグループごとに異なるスムーズを推定
# `group`をパラメトリック項にも加えることで、各曲線の平均的な高さ(切片)も
# グループごとに異なることを許容します。
gam_mod3 <- gam(y ~ group + s(x, by = group), data = sample_data_s)
print(summary(gam_mod3))
# 結果のプロット (2つのプロットが生成される)
par(mfrow = c(1, 2))
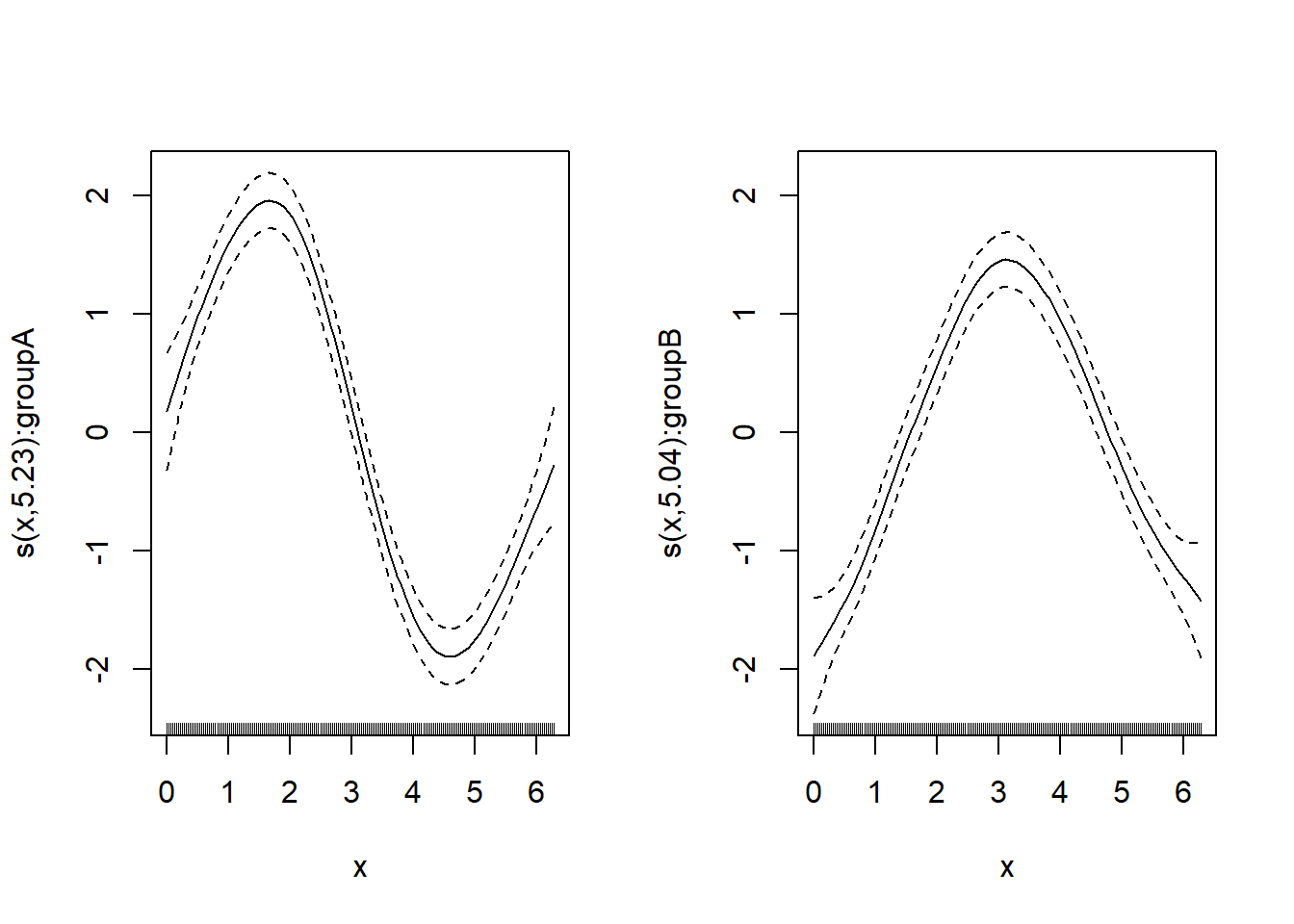
plot(gam_mod3, shade = TRUE)--- モデル3: by=group でグループ別に平滑化 ---
Family: gaussian
Link function: identity
Formula:
y ~ group + s(x, by = group)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.03563 0.05722 -0.623 0.534
groupB 0.96671 0.08092 11.946 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(x):groupA 5.226 6.346 93.27 <2e-16 ***
s(x):groupB 5.044 6.145 54.28 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.73 Deviance explained = 73.8%
GCV = 0.6756 Scale est. = 0.65488 n = 400Formula: y ~ group + s(x, by = group)
- このモデル式は、
gam_mod1やgam_mod2とは根本的に異なり、以下の2つの要素で構成されています。-
group:group変数が線形項(パラメトリック項)としてモデルに含まれています。こちらは、グループAとグループBの平均的な高さの違い(切片の差)を捉える役割を果たします。 -
s(x, by = group):s()関数にby = groupという引数を指定しています。こちらは、xとyの関係を示す曲線の形状自体が、グループAとグループBでそれぞれ異なることを許容する項です。
-
- この2つの項を組み合わせることで、モデルは「グループ間で曲線の平均的な高さも形状も異なる」という、シミュレーションデータが持つ構造を表現できるようになります。
Parametric coefficients:
- 線形項に関する情報です。
-
(Intercept):group変数の基準水準(ベースライン)であるグループAの切片に相当します。 -
groupB: グループAと比較した際の、グループBの切片の差を示します。0.96671という推定値は、グループBの曲線がグループAの曲線よりも平均的に約0.97高い位置にあることを意味します。p値が<2e-16と有意水準を下回っているため、この高さの違いは統計的に有意です。サンプルデータ生成時にグループBの関数に+1の切片項を加えた設定を、モデルが検出したことを示しています。
Approximate significance of smooth terms:
- 平滑化項の評価です。
by引数を使用した結果、平滑化項が2つに分割されている点が特徴です。 -
s(x):groupA: グループAのデータのみに対するxの平滑化項です。- edf (有効自由度):
5.226と高い値となっており(1よりも大きな値となっており)、グループAのデータが持つ非線形なsin波の形状を捉えるために、モデルが十分な柔軟性を使用したことを示します。 - p-value:
<2e-16であり、グループAにおけるxとyの間の非線形な関係が、統計的に有意であることを示しています。
- edf (有効自由度):
-
s(x):groupB: グループBのデータのみに対するxの平滑化項です。- edf (有効自由度): こちらも
5.044と高い値であり、グループBのデータが持つ非線形なcos波の形状を捉えたことを示唆しています。 - p-value:
<2e-16であり、グループBにおいてもxの効果が有意であることを示しています。
- edf (有効自由度): こちらも
モデル全体の適合度
- R-sq.(adj) = 0.730: 調整済み決定係数が
0.73、つまり73.0%という高い値です。gam_mod1(28.9%) やgam_mod2(20.0%) と比較して、適合度が改善しました。これは、モデルがデータのばらつきの大部分を説明できるようになったことを意味します。 - Deviance explained = 73.8%: 逸脱度の説明率も同様に73.8%と高い値です。
- GCV = 0.6756: GCVスコアは
0.6756であり、gam_mod1(1.7484) やgam_mod2(1.9543) よりも低下しました。GCVスコアは小さいほどモデルの予測性能が良いとされるため、gam_mod3が他のモデルに比べて優れたモデルであることを示しています。
総括
gam_mod3のサマリーは、適切なモデル構造を定義することの重要性を示しています。
-
by引数を用いることで、シミュレーションデータが持つ「グループごとにxとyの関係が異なる」という本質的な構造をモデルに組み込むことに成功しました。 - その結果、Figure 3 の通り、モデルはグループAのsin波とグループBのcos波という、全く異なる2つの関数形を推定することができました。その事実は、調整済み決定係数が73%という高い値に達したことからも裏付けられます。
結論として、gam_mod3はデータの構造を的確に捉えた、統計的に信頼性が高く、説明力も優れたモデルであると評価できます。s()関数のby引数が、このような交互作用構造、つまりyとxの間の関数関係がgroupの水準に依存して変化する構造をモデリングする上でいかに重要であるかを示す結果と言えるでしょう。
以上です。