Rの関数:brm {brms}

1. モデルの基本情報

このセクションは、実行された分析の設計図を示します。

• Family: gaussian:

  目的変数heightの分布として正規分布（ガウス分布）を仮定していることを示します。

• Links: mu = identity:

  リンク関数がidentity（恒等）であることを意味し、モデルが身長の期待値muを直接予測することを示します。

• Formula:

  このモデルの構造を定義する部分です。

  • height ~ Asym/(1 + exp(-(day - xmid)/scal)):

    モデルの非線形な部分で、身長heightがロジスティック成長曲線に従うことを定義しています。Asym、xmid、scalがこの曲線の形状を決めるパラメータです。

  • Asym ~ 1 + (1 | group):

    パラメータAsym（最終的な身長）が、集団全体の平均（1で示される切片）と、個体groupごとのばらつき（(1 | group)で示されるランダム効果）によって決まることを示しています。

  • xmid ~ 1 + (1 | group):

    同様に、パラメータxmid（成長の変曲点）も、集団平均と個体ごとのばらつきを持つことを示します。

  • scal ~ 1:

    パラメータscal（成長の速さ）は、個体差を考慮しない単一の集団平均値としてモデル化されていることを示します。

• Data:

    使用されたデータフレーム sim_data と、観測数150であることがわかります。

• Draws:

    MCMCサンプリングの設定です。4つのチェーンで、ウォームアップ後に各チェーン1000サンプル、合計で4000の事後分布サンプルが得られたことを示します。

2. Multilevel Hyperparameters (グループ（個体）レベルの効果)

このセクションは、モデルの階層構造、つまり、個体差の大きさを定量化したものです。「ハイパーパラメータ」とは、パラメータの分布を制御するパラメータを意味します。

• sd(Asym_Intercept):

  個体ごとのAsym（最終的な身長）が、集団平均の周りでどの程度ばらついているかを示す標準偏差の推定値です。Estimateが12.11であり、シミュレーションで設定した真の値（sd_asym = 20）をその信用区間（7.21 – 20.25）内に捉えています。

• sd(xmid_Intercept):

  個体ごとのxmid（成長のタイミング）のばらつきの標準偏差です。Estimateが3.00であり、こちらも真の値（sd_xmid = 2）を信用区間（1.84 – 5.09）内に捉えています。

3. Regression Coefficients (集団レベルの効果)

一般的に固定効果（Fixed Effects）と呼ばれる部分で、集団全体の平均的な成長パターンを示します。

• Asym_Intercept:

  集団全体で平均したAsym（最終的な身長）の推定値です。Estimateが98.98であり、真の値（pop_asym = 100）に近い値が推定されています。

• xmid_Intercept:

  集団全体で平均したxmid（成長のタイミング）の推定値です。Estimateが8.45であり、真の値（pop_xmid = 8）を信用区間内に捉えています。

• scal_Intercept:

  集団全体で共通のscal（成長の速さ）の推定値です。Estimateが1.46であり、真の値（pop_scal = 1.5）とほぼ一致しています。

4. Further Distributional Parameters (その他の分布パラメータ)

上記の構造では説明しきれない、データのばらつき（ノイズ）に関するパラメータです。

• sigma:

  観測誤差の標準偏差の推定値です。個々のデータ点が、モデルが予測する成長曲線から平均してどの程度離れているかを示します。Estimateが5.36であり、真の値（pop_sigma = 5）をほぼ再現しています。

MCMC診断指標

各パラメータの右側にあるRhat, Bulk_ESS, Tail_ESSは、推定結果の信頼性を担保するための診断指標です。

• Rhat:

  すべてのパラメータで1.00または1.01となっており、MCMCのチェーンが正しく同じ分布に収束したことを示しています。

• Bulk_ESS, Tail_ESS:

  実効サンプルサイズを示します。値が大きいほど、より安定した推定ができていることを意味し、今回の結果に問題は見られません。

# 4. モデルの予測結果の可視化
# --- 集団レベルの平均的な成長曲線を描画します ---
me_plot <- conditional_effects(fit_brm_nl)

plot_pop_fit <- plot(me_plot, plot = FALSE)[[1]] +
  geom_point(
    data = sim_data,
    aes(x = day, y = height),
    alpha = 0.3,
    inherit.aes = FALSE
  ) +
  labs(
    title = "集団レベルでの平均的な成長曲線と95%信用区間",
    x = "日数",
    y = "身長"
  ) + theme_bw()
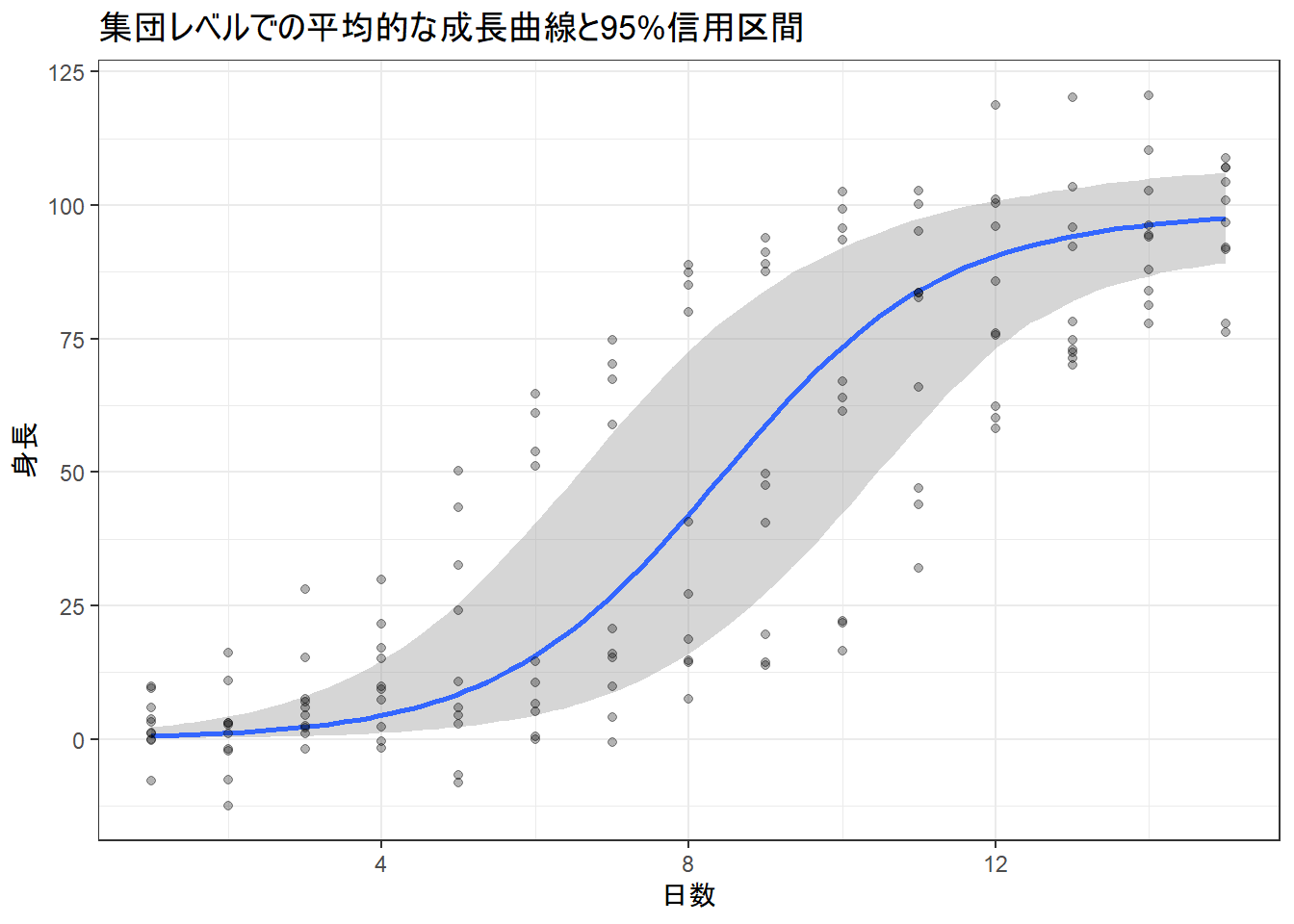
print(plot_pop_fit)

Figure 1 は、構築した階層非線形モデルが、個体差をならした（平均化した）上で、この植物集団全体の平均的な成長パターンをどのように捉えているかを視覚化するものです。

個々の植物がどのように成長するかではなく、「この品種の植物は、平均的に見れば、このようなS字カーブを描いて成長する」という、集団レベルでの大きなトレンドを明らかにすることを目的とします。

1. 黒色の点 (観測データ)

• シミュレーションで作成したすべての個体（10個体分）の、すべての観測データを一つのグラフ上にプロットしたものです。
• 個体差（最終的な身長や成長タイミングの違い）が大きいため、データは全体的に広くばらついて見えます。

2. 青色の実線 (平均的な成長曲線)

• モデルが推定した集団レベルでの平均的な成長曲線です。
• モデルの要約結果におけるPopulation-Level Effects（Asym_Intercept, xmid_Intercept, scal_Intercept）の推定値に基づいて描画されています。それゆえ、特定の個体ではなく、この集団における「架空の平均的な個体」の成長予測を示しています。
• データの中心を貫く滑らかなS字状（ロジスティック曲線）を描いていることから、モデルがデータの持つ非線形なトレンドを学習していることがわかります。

3. 灰色の帯 (平均予測に対する95%信用区間)

• 平均的な成長曲線（青い線）そのものに対する不確実性を示す95%信用区間（Credible Interval）です。
• rstanarmの例で見た「事後予測区間」とは異なります。事後予測区間が「新しいデータ点1つがどこに現れるか」の範囲を示すのに対し、この信用区間は「集団の真の平均成長曲線が、95%の確率でこの帯の範囲内に存在する」という、平均値の不確実性を示しています。それゆえ、データ全体のばらつきよりも狭い範囲となります。
• この帯の幅は、モデルがAsym_Interceptなどの集団レベルパラメータをどの程度の確信度で推定できたかを反映しています。幅が狭いほど、平均的な成長パターンに対するモデルの確信度が高いことを意味します。

総合的な解釈

1. 全体トレンドの的確な把握:

   青色の平均成長曲線は、広く散らばった黒いデータ点のちょうど中心を滑らかに貫いています。これは、個体差という大きな変動の中から、モデルが集団に共通する基本的な成長パターン（S字カーブ）を抽出できていることを示しています。

2. モデルの適合度の高さ:

   観測されたデータ点は、予測された平均曲線の上下に偏りなく分布しています。もしモデルの仮定（例えばロジスティック曲線という形状）がデータと合っていなければ、ある区間ではデータが系統的に予測線の上側に、別の区間では下側に外れる、といったパターンが見られますが、そのような兆候はありません。

# --- 個体ごとの成長曲線を描画します ---

# 1. conditions引数に渡すためのデータフレームを作成します。
#    プロットを描画したいグループの一覧を`group`列に含めます。
make_conditions <- data.frame(group = unique(sim_data$group))

# 2. conditional_effectsを呼び出します。
#    effectsに主効果 "day" を、conditionsにグループ一覧を指定します。
ce_plot <- conditional_effects(
  fit_brm_nl,
  effects = "day",
  conditions = make_conditions,
  re_formula = NULL # 全てのランダム効果を考慮に含める(デフォルト)
)

# 3. プロットを描画します。
plot_group_fit <- plot(ce_plot, plot = FALSE, ask = FALSE)[[1]] +
  geom_point(
    data = sim_data,
    aes(x = day, y = height),
    alpha = 0.3,
    inherit.aes = FALSE
  ) +
  labs(
    title = "個体ごとの成長曲線と95%信用区間",
    x = "日数",
    y = "身長"
  ) +
  # 描画領域を個体ごとに分割します
  facet_wrap(~group) + theme_bw()

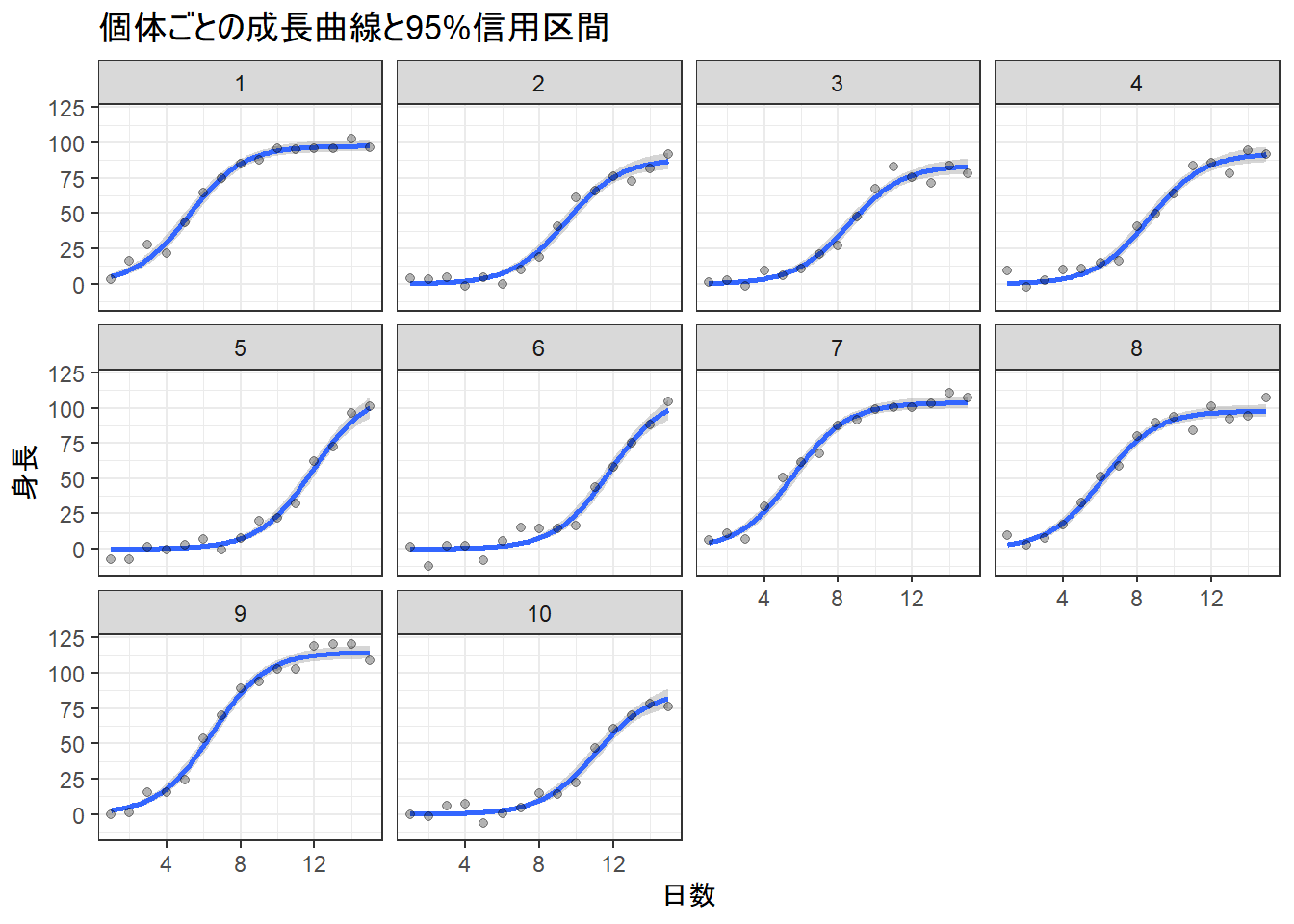
print(plot_group_fit)

Figure 2 は、Figure 1 が集団全体の「平均像」を描いたのに対し、Figure 2 は個々の植物が持つユニークな成長パターンを、モデルがどのように捉えたかを明らかにします。

「集団として共通の成長パターン（S字カーブ）を持ちながらも、個体ごとに最終的な身長や成長のタイミングは異なる」という、データの階層構造そのものを視覚化することを目的とします。

1. 10個のパネル

• グラフ全体が、番号1から10が振られた10個の小さなパネルに分割されています。
• 各パネルが、シミュレーションデータにおける一個体 (group) に対応しています。これにより、個体ごとの振る舞いを直接比較・検討することが可能になります。

2. 各パネル内の要素

各パネルの中には、集団レベルのプロットと同様の要素が描かれていますが、その意味合いは個体に特化しています。

• 黒色の点: そのパネルに対応する特定の一個体から観測された、実際の身長データです。
• 青色の実線: モデルが予測した、その個体のためだけの成長曲線です。この線は、集団全体の平均パラメータと、その個体特有のランダム効果（Asymとxmidの平均からのズレ）の両方を考慮して描画されています。
• 灰色の帯: その個体の平均予測に対する95%信用区間です。モデルが、その個体の成長曲線をどの程度の不確実性を持って予測しているかを示します。

総合的な解釈

1. 個体差の表現

• 最終身長 (Asym) の違い:

  例えば、パネル1や7の個体は、身長が約100で頭打ち（飽和）になる曲線が描かれています。一方で、パネル5や6の個体は、それよりも高く、100を超えて成長する曲線が予測されています。

• 成長タイミング (xmid) の違い:

  パネル8の個体は、比較的早い段階（日数が8より前）で成長の勢いが最大になっているように見えます。対照的に、パネル10の個体は、成長が本格化するのが少し遅いようです。

  このように、モデルがAsym ~ 1 + (1 | group)とxmid ~ 1 + (1 | group)という式で指定された通り、個体ごとに異なるAsymとxmidの値を推定し、それに基づいて個別の予測を行っていることが確認できます。

2. 「情報の共有」による推定

   各個体のデータは15点しかありませんが、モデルは滑らかで妥当な成長曲線を推定できています。これは階層モデルの「情報の共有」（Partial Pooling）という特性のおかげです。

   各個体の曲線は、その個体自身のデータ点にフィットしようとすると同時に、集団全体の平均的な成長パターンからも情報を「借りて」います。それゆえ、個々のデータのノイズに過剰に適合することなく、全体として、より安定した予測が可能になります。

以上です。