Rの関数から gam {mgcv} を確認します。
gam関数とは
gam関数は、一般化加法モデル(Generalized Additive Model, GAM)をフィッティングするためのRの関数です。
なお、一般化加法モデルとは、一般化線形モデル(GLM)を拡張し、応答変数と説明変数の間の非線形な関係を捉えることができる統計モデルです。
gam関数の引数
library(mgcv)
args(gam)function (formula, family = gaussian(), data = list(), weights = NULL,
subset = NULL, na.action, offset = NULL, method = "GCV.Cp",
optimizer = c("outer", "newton"), control = list(), scale = 0,
select = FALSE, knots = NULL, sp = NULL, min.sp = NULL, H = NULL,
gamma = 1, fit = TRUE, paraPen = NULL, G = NULL, in.out = NULL,
drop.unused.levels = TRUE, drop.intercept = NULL, nei = NULL,
discrete = FALSE, ...)
NULLformula:モデルの構造を定義する式です。
glmと同様の線形項に加え、mgcv::s()やmgcv::te()といった平滑化項を含めることができます。複数の線形予測子を持つモデル(例:gaulssファミリー)では、式のリストを渡します。family:応答変数の誤差分布とリンク関数を指定するファミリーオブジェクトです。
gaussian()(正規分布)、poisson()(ポアソン分布)、binomial()(二項分布)などに加え、mgcvパッケージ独自の拡張ファミリー(例:mgcv::nb()(負の二項分布)、mgcv::tw()(Tweedie分布))も利用できます。data:モデルで使用するデータを含むデータフレームまたはリストです。
method:平滑化パラメータを推定する方法を指定します。デフォルトは
"GCV.Cp"で、スケールパラメータが未知の場合はGCV、既知の場合はCp(マローズのCp)を用います。その他、"REML"(制限付き最尤法)や"ML"(最尤法)なども利用できます。weights:観測値ごとの重みを指定します。
subset:フィッティングに使用するデータのサブセットを指定します。
na.action:データに欠損値(NA)が含まれる場合の処理方法を指定します。
offset:モデルに含めるオフセット項を指定します。
optimizer:平滑化パラメータ選択規準を最適化するための数値的な手法を指定します。
control:フィッティングの挙動を制御するためのパラメータリストです。
scale:スケールパラメータを固定したい場合に正の値を指定します。負の値は未知、0は
poissonとbinomialでは1、それ以外では未知と判断されます。select:TRUEに設定すると、各平滑化項にさらなるペナルティが追加され、モデル選択の過程で項が完全にモデルから除外される(効果がゼロになる)可能性があります。knots:平滑化基底を構築するためのノットの位置をユーザーが指定するためのリストです。
sp:平滑化パラメータの値を直接指定します。負の値を設定したパラメータはデータから推定され、正の値は固定値として扱われます。
gamma:1より大きい値を設定すると、より平滑なモデルが選択されるようになります。GCV/UBRE/AICスコアにおける有効自由度に乗算されます。
fit:FALSEに設定すると、モデルのフィッティングは行われず、フィッティングに必要な設定情報を含むオブジェクトが返されます。
シミュレーションによるgam関数の確認
gam関数がどのように非線形関係を捉えるかを確認するために、シミュレーションデータを作成し、モデルを当てはめてみます。
なお、有意水準は5%とします。
サンプルデータの作成
ここでは、応答変数 y が3つの説明変数 x1, x2, x3 と以下のような関係を持つデータを生成します。
-
x1:yと非線形(sin波)の関係を持つ。 -
x2:yと線形の関係を持つ。 -
x3:yに影響を与えないノイズ変数。
生成されたデータには、正規分布に従う誤差を加えます。
# シミュレーションのためのサンプルデータ作成
seed <- 20251113
set.seed(seed) # 再現性のための乱数シード固定
n <- 200 # データ点数
# 説明変数の生成
x1 <- runif(n, 0, 10)
x2 <- runif(n, 0, 5)
x3 <- runif(n, 0, 1) # y には影響しない変数
# 応答変数 y の真の関数関係を定義
# f1(x1) は非線形、f2(x2) は線形
true_f1 <- 2 * sin(x1 * pi / 5)
true_f2 <- 0.5 * x2
mu <- true_f1 + true_f2
# 誤差を加えて観測データ y を生成
noise <- rnorm(n, mean = 0, sd = 1.5)
y <- mu + noise
# データフレームにまとめる
sample_data <- data.frame(y, x1, x2, x3)
# 生成したデータの一部を確認
cat("--- 生成されたサンプルデータの一部を確認 ---\n")
print(str(sample_data))--- 生成されたサンプルデータの一部を確認 ---
'data.frame': 200 obs. of 4 variables:
$ y : num 1.989 -1.454 3.097 -0.757 3.683 ...
$ x1: num 4.57 6.7 5.1 6.27 5.71 ...
$ x2: num 2.299 3.239 2.418 0.423 4.3 ...
$ x3: num 0.299 0.639 0.864 0.552 0.273 ...
NULL gam関数によるモデリングと結果の解釈
作成したサンプルデータに対してgam関数を適用します。モデル式には、各説明変数の平滑化項 s() を含めます。
# GAMモデルのフィッティング
# y ~ s(x1) + s(x2) + s(x3)
# 各説明変数が応答変数yにどのように影響するかを平滑化項s()を用いてモデル化します。
# method = "REML" は、平滑化パラメータの推定に制限付き最尤法を用いることを指定します。
gam_model <- gam(y ~ s(x1) + s(x2) + s(x3), data = sample_data, method = "REML")
# モデルのサマリーを出力
cat("--- GAMモデルのサマリー ---\n")
print(summary(gam_model))--- GAMモデルのサマリー ---
Family: gaussian
Link function: identity
Formula:
y ~ s(x1) + s(x2) + s(x3)
Parametric coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.2208 0.1093 11.16 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Approximate significance of smooth terms:
edf Ref.df F p-value
s(x1) 5.107 6.215 33.81 <2e-16 ***
s(x2) 1.000 1.000 51.47 <2e-16 ***
s(x3) 1.000 1.001 1.27 0.261
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
R-sq.(adj) = 0.541 Deviance explained = 55.7%
-REML = 379.42 Scale est. = 2.3911 n = 200Family: gaussian / Link function: identity
Family: gaussian:
モデルが応答変数
yの誤差構造として「正規分布(ガウス分布)」を仮定していることを示します。サンプルデータはrnorm()を用いて誤差を生成していますので、適切な設定です。Link function: identity:
応答変数の期待値(予測値)と、説明変数から計算される予測子(線形予測子)が、恒等関数(
identity)で結びつけられていることを意味します。言い換えれば、E[y] = (切片) + f(x1) + f(x2) + f(x3)という直接的な関係をモデル化していることを示します。こちらもシミュレーションの設定と一致しています。
Formula: y ~ s(x1) + s(x2) + s(x3)
- こちらはモデルを構築する際に指定した式そのものです。応答変数
yを、x1,x2,x3それぞれの平滑化項の和としてモデル化していることを表しています。
Parametric coefficients:
- こちらのセクションは、モデルに含まれる線形(パラメトリック)な項の係数に関する情報です。今回のモデルでは、平滑化項以外の線形項は切片
(Intercept)のみです。 - Estimate: 切片の推定値は
1.2208です。 - Pr(>|t|): p値は
<2e-16と設定した有意水準を下回っています。
Approximate significance of smooth terms:
- こちらは、各平滑化項の評価を示しています。
- s(x1):
- edf (有効自由度):
5.107となっており、1よりも大きい値です。これは、x1とyの関係が非線形であることをモデルが捉えたことを意味します。モデルは、この関係を表現するために約5つの自由度を使用しました。 - p-value:
<2e-16と設定した有意水準より小さく、x1の平滑化項が統計的に有意であり、yの予測に貢献していることを示しています。
- edf (有効自由度):
- s(x2):
- edf (有効自由度):
1.000となっており、値が正確に1です。これは、x2とyの関係が線形(直線)であるとモデルが判断したことを意味します。平滑化項の罰則(ペナルティ)が強く働き、曲線が直線まで平滑化された結果です。サンプルデータ生成において設定した線形関係を捉えています。 - p-value:
<2e-16と設定した有意水準を下回っており、x2の項も統計的に有意です。
- edf (有効自由度):
- s(x3):
- edf (有効自由度):
1.000となっており、こちらも線形の関係が推定されています。 - p-value:
0.261となっており、設定した有意水準を上回っています。それゆえ、この項は統計的に有意ではないと判断されます。モデルは、シミュレーションで意図した通り、x3がyに対して意味のある影響を与えていない(ノイズ変数である)ことを捉えています。
- edf (有効自由度):
モデル全体の適合度
R-sq.(adj) = 0.541:
調整済み決定係数で、モデルがデータ全体のばらつきの約54.1%を説明できていることを示します。
Deviance explained = 55.7%:
逸脱度の説明率で、こちらもモデルの適合度を表す指標です。
-REML = 379.42:
モデルの平滑化パラメータを推定する際に最適化された制限付き最尤法のスコアです。
Scale est. = 2.3911:
残差の分散(σ²)の推定値です。平方根を取ると
sqrt(2.3911) ≈ 1.546となり、シミュレーションで設定したノイズの標準偏差sd = 1.5に近い値です。n = 200:
モデルの学習に使用されたデータ点の数です。
モデリング結果の可視化
plot()関数を用いることで、推定された各平滑化関数を視覚的に確認できます。
# 結果のプロット
# 2x2のグラフィックレイアウトを設定
par(mfrow = c(2, 2))
# 1. s(x1) のプロットと真の関数の重ね描き
# select = 1 で最初の平滑化項を指定し、residuals = TRUE で部分残差をプロットします。
plot(gam_model, select = 1, residuals = TRUE, shade = TRUE, main = "s(x1) と真の関数", ylab = "効果")
# points() で真の関数(中心化済み)を赤色の点線で上描きします。
points(sort(x1), true_f1[order(x1)] - mean(true_f1), type = "l", col = "red", lty = 2, lwd = 2)
legend("topright", legend = "真の関数", col = "red", lty = 2, lwd = 2, bty = "n")
# 2. s(x2) のプロットと真の関数の重ね描き
# こちらも同様に、s(x2)のプロットと真の関数を重ねます。
plot(gam_model, select = 2, residuals = TRUE, shade = TRUE, main = "s(x2) と真の関数", ylab = "効果")
points(sort(x2), true_f2[order(x2)] - mean(true_f2), type = "l", col = "red", lty = 2, lwd = 2)
legend("topleft", legend = "真の関数", col = "red", lty = 2, lwd = 2, bty = "n")
# 3. s(x3) のプロット
# この項には比較対象の真の関数がないため、通常通りプロットします。
plot(gam_model, select = 3, residuals = TRUE, shade = TRUE, main = "s(x3)")
# 4. モデルの診断プロットとして残差のQ-Qプロットを描画
# qq.gam() はGAMモデルの残差が正規分布に従うかを視覚的に確認するための関数です。
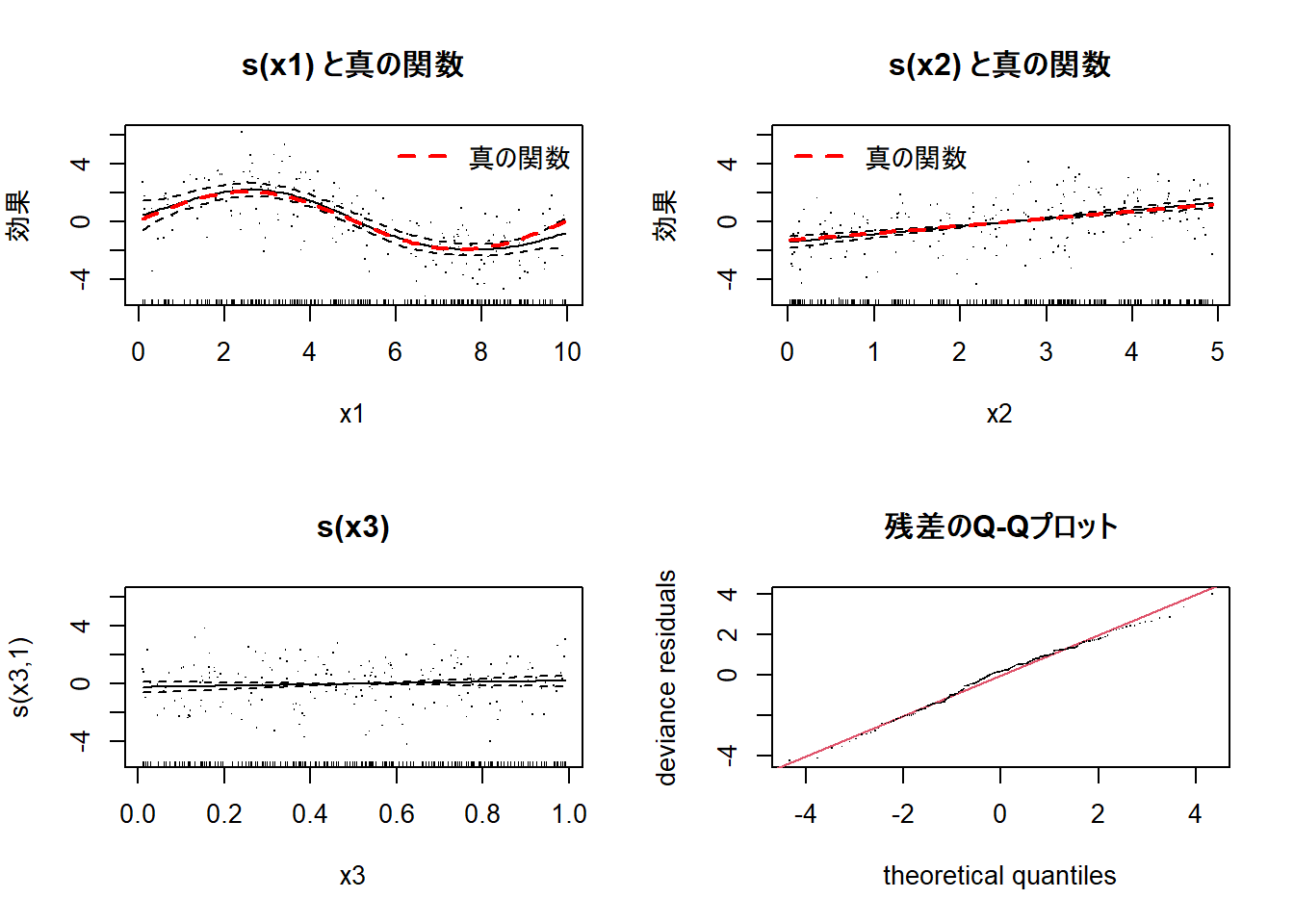
qq.gam(gam_model, main = "残差のQ-Qプロット")1. 左上: s(x1) と真の関数
説明変数x1が応答変数に与える非線形の効果を示しています。
- 実線: GAMによって推定された
x1の平滑化関数です。 - 点線(黒): 推定された関数の95%信頼区間です。
- 点線(赤): シミュレーションで設定した真のsin波の関数(
true_f1)です。 - 点群: 部分残差です。各データ点が、他の変数の効果を取り除いた後に、この平滑化曲線からどれだけ離れているかを示します。
- X軸下の短い縦線(ラグプロット):
x1のデータが存在する位置を示します。
推定された実線が、真の関数である赤色の点線を追従していることがわかります。これは、summary()でs(x1)の有効自由度(edf)が5.107と高かったことと一致し、GAMがx1とyの間の非線形な関係を捉えられたことを視覚的に示唆しています。
2. 右上: s(x2) と真の関数
説明変数x2が応答変数に与える効果を示しています。
- 実線:
x2の平滑化関数ですが、ほぼ直線になっています。 - 点線(赤): シミュレーションで設定した真の線形関数(
true_f2)です。
推定された関数(実線)はほぼ完全な直線であり、真の線形関数(赤色の点線)と重なっています。これは、summary()でs(x2)の有効自由度(edf)が1.000であったことの視覚的な裏付けです。モデルはs(x2)を罰則化(ペナルティ)によって平滑にし、データが示す単純な線形関係を正しく抽出しました。
3. 左下: s(x3)
説明変数x3の効果を示しています。
推定された関数は、y=0のライン上でほぼ水平になっています。さらに、95%信頼区間(黒の点線)が、x3の全範囲にわたって常に0を含んでいることです。これは、x3がyに対して統計的に有意な影響を与えていないことを意味します。summary()でs(x3)のp値が0.261と高かった結果と一致しており、モデルがx3を効果のないノイズ変数として判断したことを示しています。
4. 右下: 残差のQ-Qプロット
モデルの仮定が満たされているかを確認するための診断図です。
- Y軸 (deviance residuals): モデルの残差(観測値と予測値の差)です。
- X軸 (theoretical quantiles): 理論的な正規分布の分位点です。
もしモデルの残差が正規分布に従うならば、プロット上の点はほぼ直線(赤色の線)上に並びます。このプロットでは、点が直線上に乗っています。これは、モデルの残差が、正規分布に従うというサンプルデータの仮定を満たしていることを示しています。
以上です。