Rの関数から hurdle {pscl} を確認します。
hurdle関数とは
hurdle(ハードル)モデルは、ゼロが非常に多く観測されるカウントデータ(ゼロ過剰データ)を分析するために用いられる統計モデルの一種です。
ハードルモデルは、データの生成プロセスを2つの段階に分けて考えます。
第1段階(ハードル部分/ゼロ決定プロセス): 観測値が「ゼロ」か「正のカウント(1以上)」かを決定する二値的なプロセスです。このハードルを越える(すなわち、正のカウントになる)かどうかをモデル化します。通常、このプロセスは二項モデル(ロジスティック回帰など)が用いられます。
第2段階(カウント部分/正の値の決定プロセス): 観測値がハードルを越えた(すなわち、正のカウントである)場合に、そのカウント数がいくつになるかを決定するプロセスです。このプロセスは、ゼロを含まないように調整された(切断された)カウントデータ分布(例えば、切断ポアソン分布や切断負の二項分布)でモデル化されます。
hurdle関数は、これら2つのプロセスをそれぞれ別の説明変数と確率分布を用いて同時にモデル化できます。それにより、なぜゼロが多くなるのかという要因と、正の値がどの程度の大きさになるのかという要因を区別して分析することが可能になります。
hurdle関数の引数
以下にhurdle関数の引数について確認します。
library(pscl)
args(hurdle)function (formula, data, subset, na.action, weights, offset,
dist = c("poisson", "negbin", "geometric"), zero.dist = c("binomial",
"poisson", "negbin", "geometric"), link = c("logit",
"probit", "cloglog", "cauchit", "log"), control = hurdle.control(...),
model = TRUE, y = TRUE, x = FALSE, ...)
NULL-
formula- モデルの構造を定義する式。
y ~ x1 + x2 | z1 + z2のように、|の左側にカウント部分のモデル式を、右側にハードル部分(ゼロ決定)のモデル式を記述します。|以降を省略した場合、両方のモデルで同じ説明変数が使用されます。
- モデルの構造を定義する式。
-
data- モデルに使用するデータフレーム。
-
subset- データの一部を使用してモデルを推定する場合に、そのサブセットを指定します。
-
na.action- データに欠損値(
NA)が含まれる場合の処理方法を指定します。
- データに欠損値(
-
weights- 各観測値に対する重みを指定します。
-
offset- モデルに含めるオフセット項を指定します。
-
dist- カウント部分の確率分布を指定します。選択肢は
"poisson"(ポアソン分布),"negbin"(負の二項分布),"geometric"(幾何分布) です。デフォルトは"poisson"です。
- カウント部分の確率分布を指定します。選択肢は
-
zero.dist- ハードル部分の確率分布を指定します。選択肢は
"binomial"(二項分布),"poisson","negbin","geometric"です。デフォルトは"binomial"です。
- ハードル部分の確率分布を指定します。選択肢は
-
link-
zero.distに"binomial"を指定した場合のリンク関数です。選択肢は"logit","probit","cloglog","cauchit","log"です。デフォルトは"logit"で、これはロジスティック回帰を意味します。
-
-
control-
optim関数による最適化の際の詳細な設定を行うためのリスト。
-
-
model,y,x- 結果のオブジェクトに、それぞれモデルフレーム、応答変数、計画行列を含めるかどうかを指定する論理値。
シミュレーション
それでは、hurdle関数を確認するためのシミュレーションを行います。
ここでは、あるオンラインサービスの「1日の追加機能利用回数」を想定したサンプルデータを作成します。
多くのユーザーは追加機能を利用しない(利用回数0)一方で、利用するユーザーはその機能の特性から複数回利用する傾向にある、という状況を考えます。
なお、有意水準は5%とします。
1. 準備
シミュレーションに必要なパッケージを読み込みます。
library(ggplot2)
library(dplyr)2. サンプルデータの作成
ハードルモデルが適している「ゼロ過剰」なカウントデータを生成します。
-
z1(ユーザーの経験年数) とz2(チュートリアルの閲覧有無) が、追加機能を利用するかどうか(ゼロか非ゼロか)に影響を与えるとします。 -
x1(ユーザーの活動レベル) とx2(前日の利用時間) が、もし機能を利用した場合に何回利用するかに影響を与えるとします。
seed <- 20251103
set.seed(seed)
n <- 2000 # サンプルサイズ
# 説明変数の生成
z1 <- rnorm(n, mean = 3, sd = 1.5) # ゼロ部分: ユーザーの経験年数
z2 <- rbinom(n, 1, 0.6) # ゼロ部分: チュートリアル閲覧有無 (1 = 閲覧, 0 = 未閲覧)
x1 <- rnorm(n, mean = 5, sd = 2) # カウント部分: ユーザーの活動レベル
x2 <- runif(n, 0, 5) # カウント部分: 前日の利用時間
# --- ハードル部分のモデル化 ---
# 経験年数が長く(z1)、チュートリアルを閲覧している(z2)ほど、機能を利用する(非ゼロになる)確率が高いと仮定
# ロジットリンク関数の逆関数 plogis() を用いて確率を計算
# 係数を設定: intercept=-2.5, z1=0.8, z2=1.2
prob_nonzero <- plogis(-2.5 + 0.8 * z1 + 1.2 * z2)
# 上記の確率に基づき、二項分布からゼロ(0)か非ゼロ(1)かを生成
is_nonzero <- rbinom(n, 1, prob_nonzero)
# --- カウント部分のモデル化 ---
# 活動レベルが高く(x1)、前日の利用時間が長い(x2)ほど、利用回数が増えると仮定
# ログリンク関数なので、exp() を用いてポアソン分布の期待値(ラムダ)を計算
# 係数を設定: intercept=0.5, x1=0.1, x2=0.2
lambda <- exp(0.5 + 0.1 * x1 + 0.2 * x2)
# 正の値のみを持つ切断ポアソン分布からカウント数を生成
# ここでは単純化のため、通常のポアソン分布からサンプリングし、0が出た場合は1に置き換える処理を行う
positive_counts <- rpois(n, lambda)
positive_counts[positive_counts == 0] <- 1 # 0を許容しない
# --- 最終的な目的変数の作成 ---
# is_nonzeroが0の場合は0、1の場合はpositive_countsの値を採用
y <- ifelse(is_nonzero == 0, 0, positive_counts)
# データフレームの作成
sim_data <- data.frame(y, x1, x2, z1, z2)
# 生成したデータの分布を確認
cat("作成した目的変数 y の要約:\n")
print(summary(sim_data$y))
cat(sprintf("\nゼロの割合: %.2f%%\n", mean(sim_data$y == 0) * 100))
# データの可視化
ggplot(sim_data, aes(x = y)) +
geom_histogram(binwidth = 1, fill = "skyblue", color = "black") +
labs(
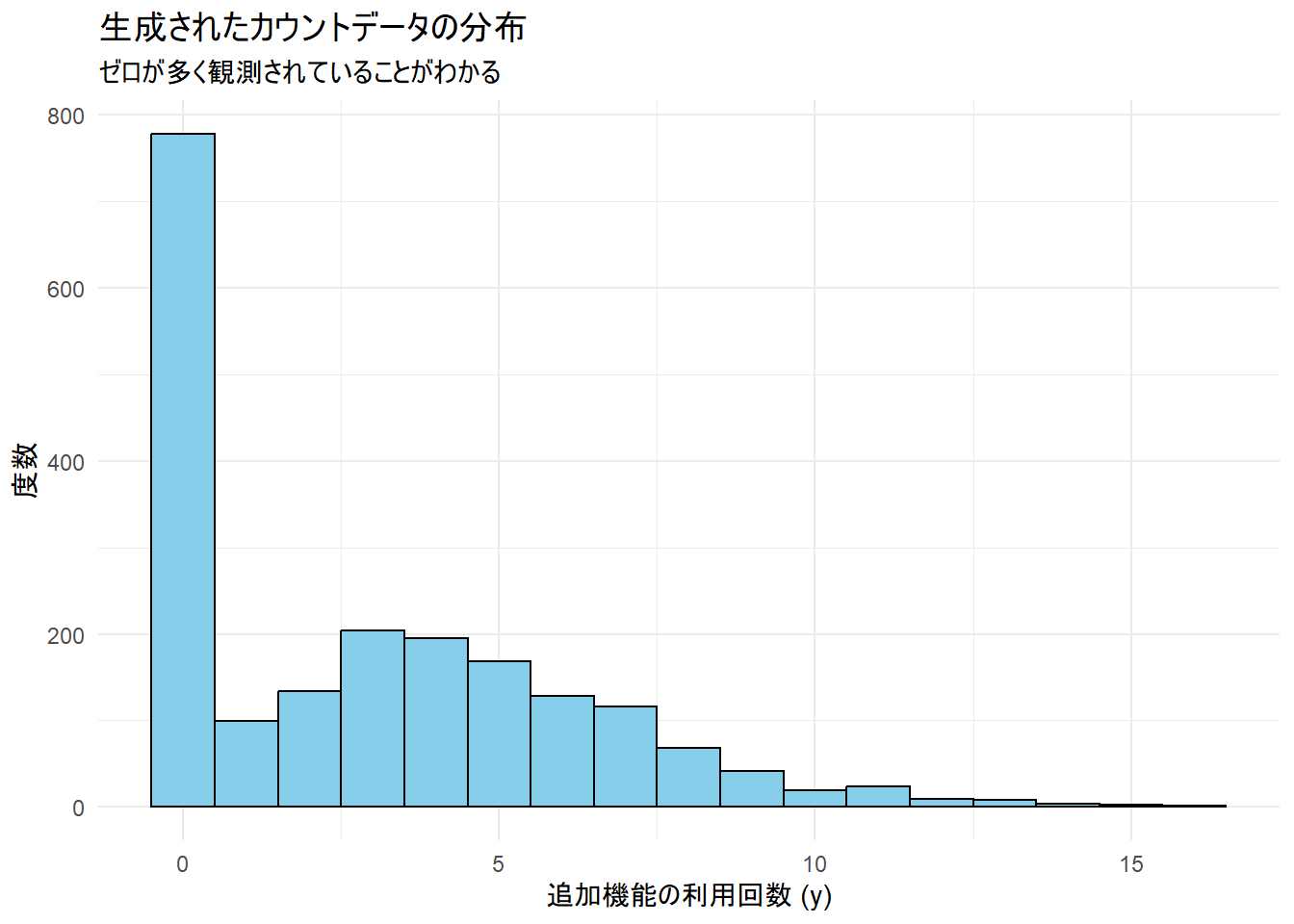
title = "生成されたカウントデータの分布",
subtitle = "ゼロが多く観測されていることがわかる",
x = "追加機能の利用回数 (y)",
y = "度数"
) +
theme_minimal()作成した目的変数 y の要約:
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 0.00 2.00 2.95 5.00 16.00
ゼロの割合: 38.85%生成されたデータは、約60%がゼロであり、ゼロ過剰な特徴を持っていることが確認できます。
3. hurdleモデルの適用
作成したサンプルデータに対してhurdleモデルを適用します。データ生成の際に仮定した通り、カウント部分のモデルにはx1とx2を、ハードル部分のモデルにはz1とz2を使用します。
# ハードルモデルの推定
# カウント部分(正の値)はポアソン分布(dist = "poisson")
# ゼロ/非ゼロのハードル部分は二項分布(zero.dist = "binomial")
hurdle_model <- hurdle(
y ~ x1 + x2 | z1 + z2,
data = sim_data,
dist = "poisson",
zero.dist = "binomial",
link = "logit"
)4. 結果の確認
モデルの推定結果をsummary()で確認します。
cat("ハードルモデルの推定結果:\n")
summary(hurdle_model)ハードルモデルの推定結果:
Call:
hurdle(formula = y ~ x1 + x2 | z1 + z2, data = sim_data, dist = "poisson", zero.dist = "binomial", link = "logit")
Pearson residuals:
Min 1Q Median 3Q Max
-2.1482 -0.7547 -0.2425 0.6453 4.2597
Count model coefficients (truncated poisson with log link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.471731 0.050536 9.334 <2e-16 ***
x1 0.103657 0.006933 14.950 <2e-16 ***
x2 0.201768 0.009686 20.830 <2e-16 ***
Zero hurdle model coefficients (binomial with logit link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.27257 0.15342 -14.81 <2e-16 ***
z1 0.74014 0.04324 17.12 <2e-16 ***
z2 1.08173 0.10781 10.03 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Number of iterations in BFGS optimization: 13
Log-likelihood: -3674 on 6 Df全体のサマリー
Call:
hurdle(formula = y ~ x1 + x2 | z1 + z2, data = sim_data, dist = "poisson",
zero.dist = "binomial", link = "logit")このCallセクションは、このモデルがどのような設定で実行されたかを示しています。
-
formula = y ~ x1 + x2 | z1 + z2:- 目的変数
yに対し、|の左側 (x1 + x2) がカウント部分を、右側 (z1 + z2) がハードル部分をモデル化するために使用されたことを意味します。
- 目的変数
-
dist = "poisson":- カウント部分(利用回数が1以上の場合)が、切断ポアソン分布に従うと仮定されています。
-
zero.dist = "binomial"とlink = "logit":- ハードル部分(利用回数が0か1以上か)が、ロジットリンク関数を用いた二項分布(ロジスティック回帰)でモデル化されていることを示します。
1. カウントモデル部分 (Count model coefficients)
Count model coefficients (truncated poisson with log link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.471731 0.050536 9.334 <2e-16 ***
x1 0.103657 0.006933 14.950 <2e-16 ***
x2 0.201768 0.009686 20.830 <2e-16 ***こちらのパートは、「もしユーザーが追加機能を利用した場合(利用回数が1回以上の場合)、その利用回数が何に影響されるか」を分析した結果です。
- 解釈:
-
(Intercept): 切片です。x1とx2が共に0のときの、対数スケールでの平均利用回数に相当します。 -
x1(ユーザーの活動レベル): 係数(Estimate)は0.103657と正の値です。これは、活動レベルが高いユーザーほど、利用回数が多くなる傾向にあることを示しています。 -
x2(前日の利用時間): 係数は0.201768とこちらも正の値です。前日の利用時間が長いユーザーほど、利用回数が多くなることを示唆しています。
-
- 統計的有意性:
-
Pr(>|z|)列の値はp値を示しています。全ての変数で2e-16より小さい(ほぼ0に近い)値になっており、設定した有意水準を下回っています。それゆえ、これらの変数が利用回数に与える影響は、偶然によるものではないと示唆されます。 - この結果から、データ生成時の設定(
x1の係数=0.1,x2の係数=0.2)をモデルが捉えられていることを確認できます。
-
2. ゼロハードルモデル部分 (Zero hurdle model coefficients)
Zero hurdle model coefficients (binomial with logit link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.27257 0.15342 -14.81 <2e-16 ***
z1 0.74014 0.04324 17.12 <2e-16 ***
z2 1.08173 0.10781 10.03 <2e-16 ***こちらのパートは、「そもそもユーザーが追加機能を利用するか、しないか(利用回数が0か、1以上か)」というハードルを越える確率が何に影響されるかを分析した結果です。
- 解釈:
-
(Intercept): 切片です。z1とz2が共に0のときの、利用する(非ゼロである)確率の対数オッズです。 -
z1(ユーザーの経験年数): 係数は0.74014と正の値です。経験年数が長いユーザーほど、機能を利用する確率(ハードルを越える確率)が高くなることを示しています。 -
z2(チュートリアル閲覧有無): 係数は1.08173とこちらも正の値です。チュートリアルを閲覧したユーザーの方が、機能を利用する確率が有意に高いことを示唆しています。
-
- 統計的有意性:
- カウントモデル部分と同様に、全ての変数のp値が設定した有意水準を下回っていることを確認できます。
- この結果からも、データ生成時の設定(
z1の係数=0.8,z2の係数=1.2)をモデルが捉えられていることを確認できます。
補足情報
-
Pearson residuals: モデルの当てはまりを診断するための残差の要約統計量です。 -
Number of iterations in BFGS optimization: 13: モデルを推定するための計算(最適化)が13回の反復で収束したことを示します。少ない回数での収束は、問題なく推定が完了したことを意味します。 -
Log-likelihood: -3674 on 6 Df: モデルの対数尤度です。モデルの適合度を示す指標であり、異なるモデルを比較する際などに用いられます。6 Dfは、モデルが6個のパラメータ(カウント部分で3個、ハードル部分で3個)を推定したことを示します。
5. 予測と可視化
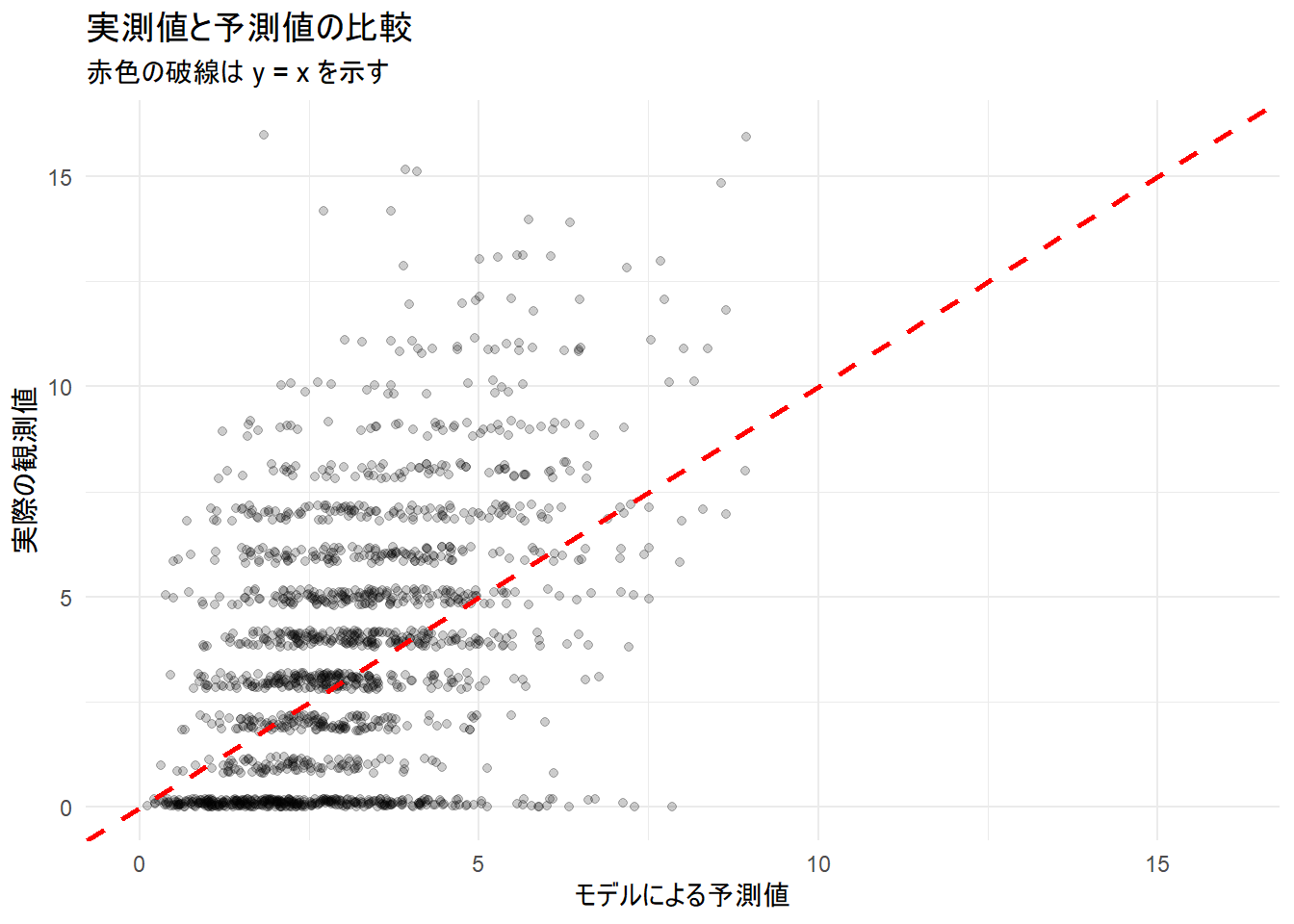
最後に、構築したモデルを用いて予測値と実測値を比較し、モデルの当てはまりを視覚的に確認します。
# 予測値の取得
sim_data$predicted <- predict(hurdle_model, type = "response")
# 実測値と予測値の比較プロット
ggplot(sim_data, aes(x = predicted, y = y)) +
geom_jitter(alpha = 0.2, width = 0.2, height = 0.2) +
geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed", size = 1) +
labs(
title = "実測値と予測値の比較",
subtitle = "赤色の破線は y = x を示す",
x = "モデルによる予測値",
y = "実際の観測値"
) +
xlim(0, max(sim_data$predicted, sim_data$y)) +
ylim(0, max(sim_data$predicted, sim_data$y)) +
theme_minimal()以上です。