Rの関数から stan_glm {rstanarm} を確認します。
stan_glm関数について
stan_glmは、Rのrstanarmパッケージに属する関数であり、ベイズ一般化線形モデル(Bayesian Generalized Linear Models)を推定するために使用されます。
本関数は、統計モデリング言語Stanをバックエンドに利用して、MCMC(マルコフ連鎖モンテカルロ法)サンプリングを実行します。
従来の最尤法を用いるglm関数と似た構文(formula, family, dataなど)で使用できるため、glmに慣れたユーザーがベイズモデリングへ移行する際の障壁が低いという利点があります。
glmがパラメータを単一の点推定値として求めるのに対し、stan_glmはパラメータの事後分布を推定します。
この事後分布を通じて、パラメータの不確実性を確率分布として評価できる点が、ベイズモデリングの特徴です。
それゆえ、サンプルサイズが小さい場合や、モデルの不確実性を厳密に評価したい場合に利用されます。
stan_glm関数の引数
以下に、stan_glm関数の引数について確認します。
formula:モデルの構造を定義するRのformulaオブジェクトです。
目的変数 ~ 説明変数1 + 説明変数2のように記述します。family:目的変数の確率分布とリンク関数を指定する
familyオブジェクトです。例えば、gaussian()(正規分布)、binomial()(二項分布)、poisson()(ポアソン分布)、Gamma()(ガンマ分布)などがあります。glm関数と同様の指定方法です。data:モデルで使用するデータが含まれたデータフレームを指定します。
weights:各観測値に対する重みを指定します。
subset:データの一部をモデル推定に使用する場合に、そのサブセットを指定します。
na.action:データに欠損値(
NA)が含まれている場合の処理方法を指定します。デフォルトでは、欠損値を持つ行は除外されます。offset:モデルに含めるオフセット項を指定します。オフセット項は、係数が1に固定された既知の変数です。例えば、ポアソン回帰で観察期間が異なる場合などに使用します。
model,x,y:それぞれ、モデルフレーム、モデル行列、目的変数を結果のオブジェクトに含めるかどうかを指定する論理値です。
contrasts:モデルに含まれる因子(カテゴリカル変数)の対比(コントラスト)を指定します。
prior:回帰係数(切片を除く)に対する事前分布を指定します。
rstanarmでは、normal(),student_t(),cauchy()などの事前分布が用意されています。事前分布を指定しない場合、モデルファミリーに応じてデフォルトの弱情報事前分布が設定されます。prior_intercept:切片に対する事前分布を指定します。係数とは別に設定することで、より柔軟なモデリングが可能になります。
prior_aux:補助パラメータに対する事前分布を指定します。例えば、正規分布モデルにおける誤差の標準偏差(σ)や、負の二項分布モデルにおける形状パラメータなどが該当します。
prior_PD:論理値であり、
TRUEに設定すると、事前分布からのみサンプリングを行います。モデルにデータがどの程度適合しているかではなく、事前分布がどのようなデータを生成するかを確認するために使用します。algorithm:パラメータを推定するためのアルゴリズムを
"sampling"、"optimizing"、"meanfield"、"fullrank"から選択します。デフォルトは"sampling"であり、マルコフ連鎖モンテカルロ法(MCMC)、特にハミルトニアン・モンテカルロ法(HMC)を用いて、パラメータの事後分布からサンプリングを行います。mean_PPD:論理値であり、
TRUEの場合、事後予測分布(Posterior Predictive Distribution)の平均を計算します。デフォルトでは、algorithmが"optimizing"でない限りTRUEです。adapt_delta:MCMCサンプリングのチューニングパラメータの一つです。目標とする平均受容確率を制御し、通常は0.8から1の間の値を指定します。発散(divergence)が多い場合に、この値を大きくする(例えば0.99に)ことで問題が改善することがあります。
QR:論理値であり、
TRUEに設定すると、予測子行列(モデル行列)に対してQR分解を適用してからモデルを推定します。これにより、予測子間に強い相関がある場合のサンプリング効率が向上することがあります。sparse:論理値であり、予測子行列がスパース(疎行列)である場合に
TRUEに設定することで、計算効率を向上させることができます。
シミュレーション
ここでは、「あるオンライン広告の1日あたりのクリック数」を目的変数とし、「広告の表示回数」を説明変数とするシミュレーションを行います。
GLMを用いる理由:
クリック数は0以上の整数値をとるカウントデータであり、正規分布を仮定する通常の線形モデルは適切ではありません。それゆえ、ポアソン分布を仮定する一般化線形モデル(ポアソン回帰)を利用します。
ベイズ推定を用いる理由:
今回は、意図的にサンプルサイズを小さく(N=40)設定します。サンプルサイズが小さい場合、最尤法による推定は不安定になりがちですが、ベイズ推定では事前分布の設定による正則化効果により、より安定した推定が期待できます。
以下に、シミュレーションを実行するためのRコードを示します。
1. サンプルデータの作成
# 必要なパッケージを読み込みます
library(rstanarm)
library(ggplot2)
library(bayesplot)
# シミュレーションのための乱数シードを設定します
seed <- 20251101
set.seed(seed)
# サンプルサイズを40と、意図的に小さく設定します
N <- 40
# 説明変数:1日の広告表示回数(単位:1000回)
# 1から20の範囲で一様分布から生成します
impressions <- runif(N, min = 1, max = 20)
# 真のパラメータを設定します
# 真の切片(表示回数が0の場合の対数クリック数)
true_beta0 <- 1.0
# 真の係数(表示回数が1単位増加した場合の対数クリック数の増加量)
true_beta1 <- 0.15
# 線形予測子を計算し、指数変換によって平均クリック数(λ)を求めます
lambda <- exp(true_beta0 + true_beta1 * impressions)
# ポアソン分布に従って目的変数(クリック数)を生成します
clicks <- rpois(n = N, lambda = lambda)
# シミュレーションデータをデータフレームに格納します
sim_data <- data.frame(impressions, clicks)
cat("--- 作成されたサンプルデータの一部を確認 ---\n")
print(str(sim_data))--- 作成されたサンプルデータの一部を確認 ---
'data.frame': 40 obs. of 2 variables:
$ impressions: num 7.83 11.37 19.25 12.87 17.12 ...
$ clicks : int 9 12 50 16 31 18 17 30 6 33 ...
NULL2. stan_glmによるポアソン回帰モデルの推定
# familyにpoisson(link = "log")を指定します
# algorithmのデフォルトは"sampling"(NUTSサンプラー)です
# MCMCのウォームアップ期間を500、サンプリングを1500に設定します
fit_stan_glm <- stan_glm(
clicks ~ impressions,
family = poisson(link = "log"),
data = sim_data,
warmup = 500,
iter = 2000,
chains = 4,
seed = seed,
refresh = 0
)3. モデル推定結果の要約
summary(fit_stan_glm)
Model Info:
function: stan_glm
family: poisson [log]
formula: clicks ~ impressions
algorithm: sampling
sample: 6000 (posterior sample size)
priors: see help('prior_summary')
observations: 40
predictors: 2
Estimates:
mean sd 10% 50% 90%
(Intercept) 0.9 0.1 0.7 0.9 1.1
impressions 0.2 0.0 0.1 0.2 0.2
Fit Diagnostics:
mean sd 10% 50% 90%
mean_PPD 21.1 1.0 19.8 21.1 22.5
The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).
MCMC diagnostics
mcse Rhat n_eff
(Intercept) 0.0 1.0 2086
impressions 0.0 1.0 2216
mean_PPD 0.0 1.0 4548
log-posterior 0.0 1.0 2319
For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).この要約は、主に4つのセクションから構成されています。
- Model Info: どのようなモデルを構築したかの概要
- Estimates: 推定されたパラメータ(回帰係数など)の詳細
- Fit Diagnostics: モデルがデータにどれだけ適合しているかの診断
- MCMC diagnostics: MCMCサンプリングが正しく機能したかの診断
以下、それぞれのセクションを確認します。
1. Model Info (モデル情報)
このセクションは、実行された分析の全体像を示します。
function: stan_glm:このモデルが
rstanarmパッケージのstan_glm関数を用いて構築されたことを示します。family: poisson [log]:モデルがポアソン回帰モデルであることを示しています。目的変数(クリック数)がポアソン分布に従うと仮定しており、リンク関数として対数(log)リンクを使用していることを意味します。
formula: clicks ~ impressions:モデルの構造式です。
clicksが目的変数であり、impressionsがその変動を説明するための説明変数であることを示します。algorithm: sampling:パラメータの推定に、MCMCサンプリング(ハミルトニアン・モンテカルロ法)が使用されたことを示します。
sample: 6000 (posterior sample size):事後分布からの総サンプルサイズです。これは
(iter - warmup) * chains、すなわち(2000 - 500) * 4 = 6000回のサンプリング結果に基づいて、以降の統計量が計算されていることを示します。priors: see help('prior_summary'):パラメータの事前分布に関する情報です。今回は明示的に指定しなかったため、
rstanarmが自動で設定したデフォルトの弱情報事前分布が使用されています。詳細はprior_summary(fit_stan_glm)により確認できます。
# 使用された事前分布の確認
prior_summary(fit_stan_glm)Priors for model 'fit_stan_glm'
------
Intercept (after predictors centered)
~ normal(location = 0, scale = 2.5)
Coefficients
Specified prior:
~ normal(location = 0, scale = 2.5)
Adjusted prior:
~ normal(location = 0, scale = 0.5)
------
See help('prior_summary.stanreg') for more detailsこの出力は、大きく分けて「切片(Intercept)」と「係数(Coefficients)」の2つの部分に関する事前分布の情報を示しています。
1. Intercept (after predictors centered) (切片の事前分布)
~ normal(location = 0, scale = 2.5)これは、切片パラメータに対する事前分布が、平均(location)が0で、標準偏差(scale)が2.5の正規分布であることを示しています。なお、
after predictors centeredとあります通り、説明変数(今回はimpressions)からその平均値を引く中心化(centering)という前処理が行われています。よって、中心化されたモデルでは、切片は「すべての説明変数がその平均値をとるときの目的変数の予測値」を意味するようになります。
2. Coefficients (係数の事前分布)
このセクションは、説明変数(今回はimpressions)の係数に対する事前分布を示しています。
Specified prior: ~ normal(location = 0, scale = 2.5)これは、
rstanarmのデフォルトで指定されている係数用の事前分布です。ユーザーが何も指定しない場合、この「平均0、標準偏差2.5の正規分布」が基本的な設定として用意されています。Adjusted prior: ~ normal(location = 0, scale = 0.5)こちらが、このモデルで実際に使用された事前分布です。デフォルトの
scale = 2.5からscale = 0.5へと自動的に調整(Adjusted)されています。今回のケースでは、impressions変数のスケールに基づき、rstanarmがscale = 0.5がより適切であると判断し、事前分布を調整しています。observations: 40:モデルの推定に使用された観測データの数(サンプルサイズ)が40であることを示します。
predictors: 2:モデルに含まれる予測子の数です。この「2」は、切片(Intercept)と説明変数
impressionsの合計です。
2. Estimates (パラメータの推定結果)
このセクションは、各パラメータの事後分布の要約統計量を示します。
- 行 (
(Intercept),impressions):-
(Intercept): 切片です。impressionsが0のときの、対数クリック数の期待値を表します。 -
impressions: 説明変数impressionsの係数です。impressionsが1単位増加したときに、対数クリック数が平均してどれだけ増加するかを示します。
-
- 列:
-
mean: 事後分布の平均値です。パラメータの点推定値としてよく用いられます。 -
sd: 事後分布の標準偏差です。この値が大きいほど、パラメータの推定に関する不確実性が高いことを意味します。 -
10%,50%,90%: 事後分布の分位点です。50%は中央値(median)であり、meanと同様に代表値として使われます。10%と90%の間には、パラメータの真の値が80%の確率で含まれると推定されます(80%信用区間)。
-
結果の解釈: impressionsの係数の平均値は0.2であり、正の値をとっています。それゆえ、「広告の表示回数が増加すると、クリック数も増加する」という正の関係性がデータから示唆されていることがわかります。
3. Fit Diagnostics (モデルの適合度診断)
このセクションは、モデルが観測データをどの程度うまく説明できているかを示します。
mean_PPD(mean of the posterior predictive distribution):事後予測分布の平均値です。これは、推定されたモデルを用いて、もし同じ条件で再度データを取得した場合に、目的変数がどのような値をとるかをシミュレーションした結果の平均です。
結果の解釈:
mean_PPDの平均値は21.1です。この値は、実際の観測データclicksの平均値と比較されるべきです。両者の値が近ければ、モデルはデータの中心的な傾向をうまく捉えられていると判断できます。
# clicks の平均値
mean(clicks)[1] 21.1754. MCMC diagnostics (MCMC診断)
このセクションは、サンプリングアルゴリズムがうまく機能し、信頼できる結果を生成したかどうかを評価するための指標です。
mcse(Monte Carlo Standard Error):モンテカルロ標準誤差です。事後分布の平均値を推定する際のシミュレーション自体に起因する誤差の大きさを示します。事後分布の標準偏差(
sd)と比較して、この値が十分に小さければ問題ありません。0.0となっているため、精度良く推定できていることがわかります。Rhat(Potential Scale Reduction Factor):MCMCの収束を診断するための指標です。複数のチェーン(今回は4つ)の結果を比較し、それらが同じ分布に収束しているかを評価します。値が1.0に近い場合、チェーンが良好に収束したと判断します。今回の結果はすべて
1.0であり、収束に関して問題ないことを示しています。n_eff(effective sample size):実効サンプルサイズです。MCMCで得られるサンプルは系列相関(自己相関)を持つため、独立なサンプルよりも情報量が少なくなります。
n_effは、得られたMCMCサンプルが、独立なサンプル何個分に相当するかの情報量を持っているかを示します。この値が大きいほど、事後分布をより安定して推定できていることを意味します。一般に数百以上あれば問題ないとされますが、今回は2000以上あり、効率的なサンプリングが行われたことを確認できます。
4. 事後分布の可視化
# 必要なパッケージを読み込みます
library(patchwork)
# 1. モデルから事後分布のサンプリングデータを抽出します
posterior_draws <- as.data.frame(fit_stan_glm)
# 2. 各パラメータの95%信用区間を計算します
intercept_ci <- quantile(posterior_draws$`(Intercept)`, probs = c(0.025, 0.975))
impressions_ci <- quantile(posterior_draws$impressions, probs = c(0.025, 0.975))
# 3. 切片(Intercept)のプロットを作成します
plot_intercept <- ggplot(posterior_draws, aes(x = `(Intercept)`)) +
# 事後分布を密度プロットとして描画
geom_density(fill = "skyblue", alpha = 0.7) +
# 95%信用区間の下限と上限を青い点線で追加
geom_vline(xintercept = intercept_ci, color = "navy", linetype = "dotted", linewidth = 1) +
# 真の値を赤い破線で追加
geom_vline(xintercept = true_beta0, color = "red", linetype = "dashed", linewidth = 1) +
labs(
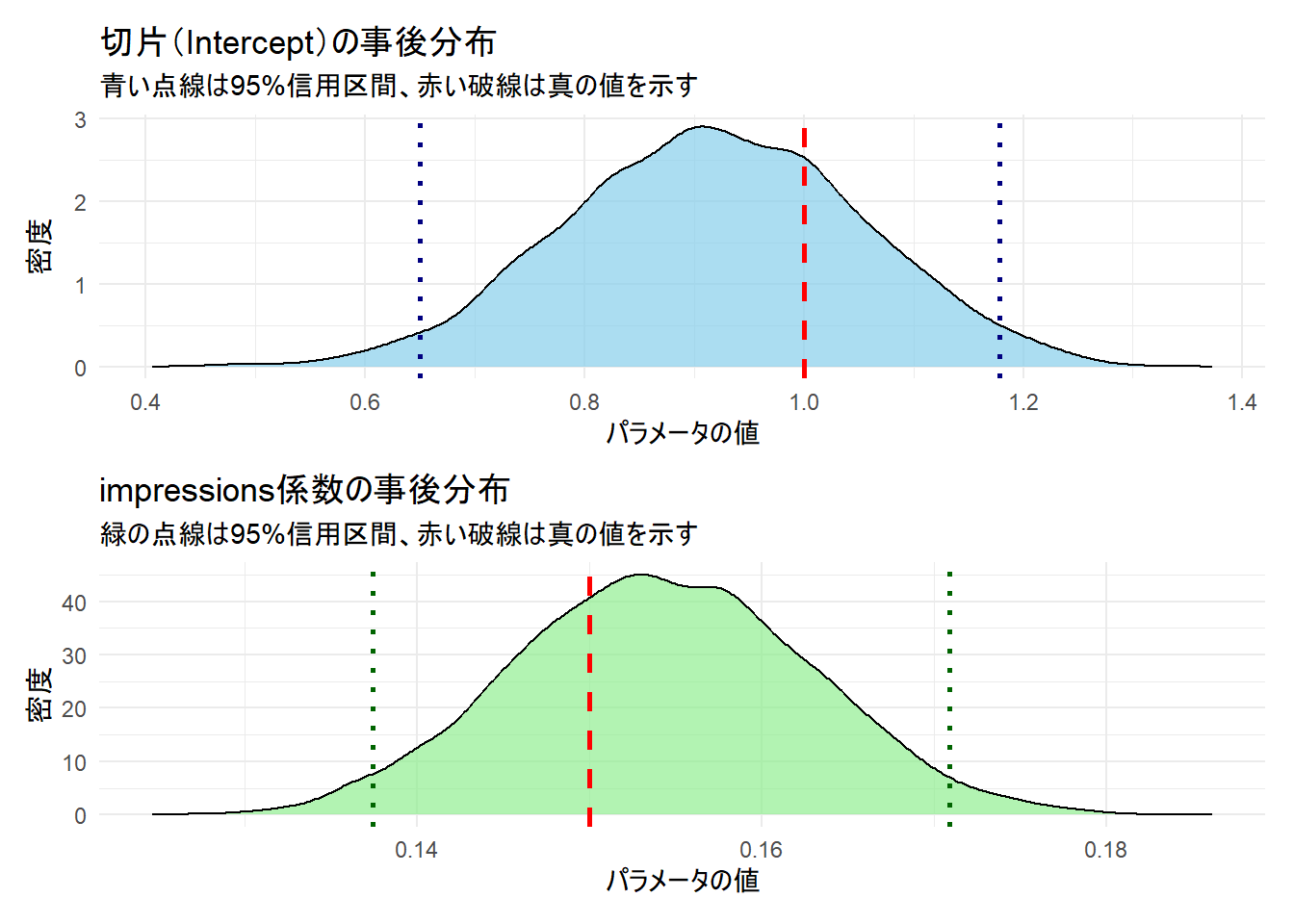
title = "切片(Intercept)の事後分布",
subtitle = "青い点線は95%信用区間、赤い破線は真の値を示す",
x = "パラメータの値",
y = "密度"
) +
theme_minimal()
# 4. impressionsのプロットを作成します
plot_impressions <- ggplot(posterior_draws, aes(x = impressions)) +
# 事後分布を密度プロットとして描画
geom_density(fill = "lightgreen", alpha = 0.7) +
# 95%信用区間の下限と上限を緑の点線で追加
geom_vline(xintercept = impressions_ci, color = "darkgreen", linetype = "dotted", linewidth = 1) +
# 真の値を赤い破線で追加
geom_vline(xintercept = true_beta1, color = "red", linetype = "dashed", linewidth = 1) +
labs(
title = "impressions係数の事後分布",
subtitle = "緑の点線は95%信用区間、赤い破線は真の値を示す",
x = "パラメータの値",
y = "密度"
) +
theme_minimal()
# 5. patchworkパッケージを使って2つのプロットを縦に並べて表示します
combined_plot <- plot_intercept / plot_impressions
# 結合したプロットを表示します
print(combined_plot)
# posterior_interval()関数を用いて95%信用区間を計算します
# 第1引数にモデルオブジェクトを、prob引数に求める確率(95%なので0.95)を指定します
cat("--- パラメータの95%信用区間 ---\n")
cred_intervals <- posterior_interval(fit_stan_glm, prob = 0.95)
print(cred_intervals)--- パラメータの95%信用区間 ---
2.5% 97.5%
(Intercept) 0.6502968 1.1787904
impressions 0.1374118 0.17088415. 事後予測チェック
# モデルがデータをうまく表現できているかを確認します
# yrepはモデルから生成された予測データセットです
pp_check_plot <- pp_check(fit_stan_glm, plotfun = "dens_overlay") +
labs(
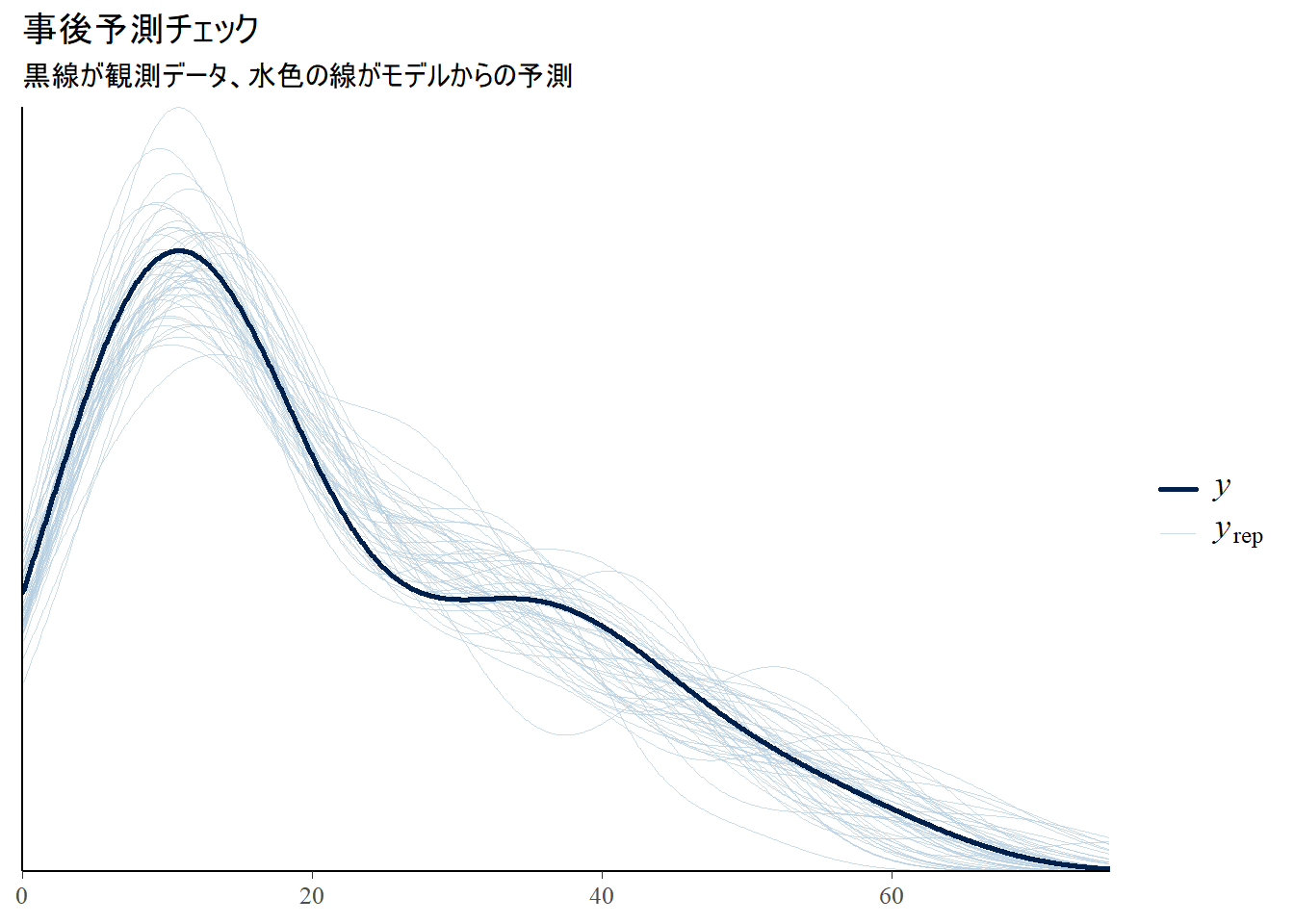
title = "事後予測チェック",
subtitle = "黒線が観測データ、水色の線がモデルからの予測"
)
print(pp_check_plot)Figure 2 の事後予測チェック(Posterior Predictive Check, PPC)は、構築したベイズモデルが現実のデータをどの程度うまく再現できるかを評価するための診断プロットです。
グラフの各要素の確認
Figure 2 は、2種類の密度プロット(データの分布を滑らかな曲線で示したもの)を重ね合わせて描画しています。
黒い太線 (
y):これは、実際に観測されたデータ(今回のシミュレーションにおける
clicks変数)の分布を示しています。この線が、我々がモデルに再現してほしい「お手本」あるいは「正解」となります。多数の水色の細線 (
y_rep):y_repは “replicated y”、すなわち「複製されたデータセット」を意味します。これは、学習済みモデルが「もし現実に似たデータがもう一度生成されたら、どのような分布になるだろうか」と、何度もシミュレーションを行った結果です。 具体的には、モデルの事後分布からパラメータ(切片と係数)のセットをランダムに抽出し、そのパラメータを使って新しいデータセットを生成する、というプロセスを繰り返します。水色の細線一本一本が、そのようにして生成された一つの仮想的なデータセットの分布に対応します。
Figure 2 の解釈は、「黒い太線が、水色の細線の集団の中に自然に紛れ込んでいるか?」を見ることにあります。
良い適合の場合:
Figure 2 を見ると、黒い太線(観測データ)は、多数の水色の細線(モデルによる予測)の集団のちょうど中心あたりに位置しており、形状も似ています。 黒い線が水色の線の中から浮き上がって見えるような、特別な外れ値にはなっていません。 この結果は、構築したポアソン回帰モデルが、観測データの分布の形状(山の位置、広がり、歪みなど)を捉えられており、データ生成のメカニズムを模倣できていることを示唆しています。
悪い適合の場合:
もしモデルの適合が悪ければ、黒い線は水色の線の束から大きく外れた位置にあるでしょう。例えば、山の位置が全く違っていたり、黒い線だけが二つの山を持つような特殊な形状をしていたりします。そのような場合、モデル(例:ポアソン分布という仮定)がデータの構造を捉えきれていないと判断し、モデルの修正を検討する必要があります。
6. 予測結果の可視化
# 観測データとモデルによる予測を重ねてプロットします
# 予測の不確実性(信用区間)も同時に描画します
predicted_draws <- posterior_predict(fit_stan_glm, newdata = sim_data)
# 95%予測区間を計算します
sim_data$pred_mean <- apply(predicted_draws, 2, mean)
sim_data$pred_lower <- apply(predicted_draws, 2, quantile, probs = 0.025)
sim_data$pred_upper <- apply(predicted_draws, 2, quantile, probs = 0.975)
# 描画します
prediction_plot <- ggplot(sim_data, aes(x = impressions)) +
geom_point(aes(y = clicks), color = "black", alpha = 0.8, size = 3) +
geom_line(aes(y = pred_mean), color = "royalblue", linewidth = 1) +
geom_ribbon(aes(ymin = pred_lower, ymax = pred_upper), alpha = 0.2, fill = "royalblue") +
labs(
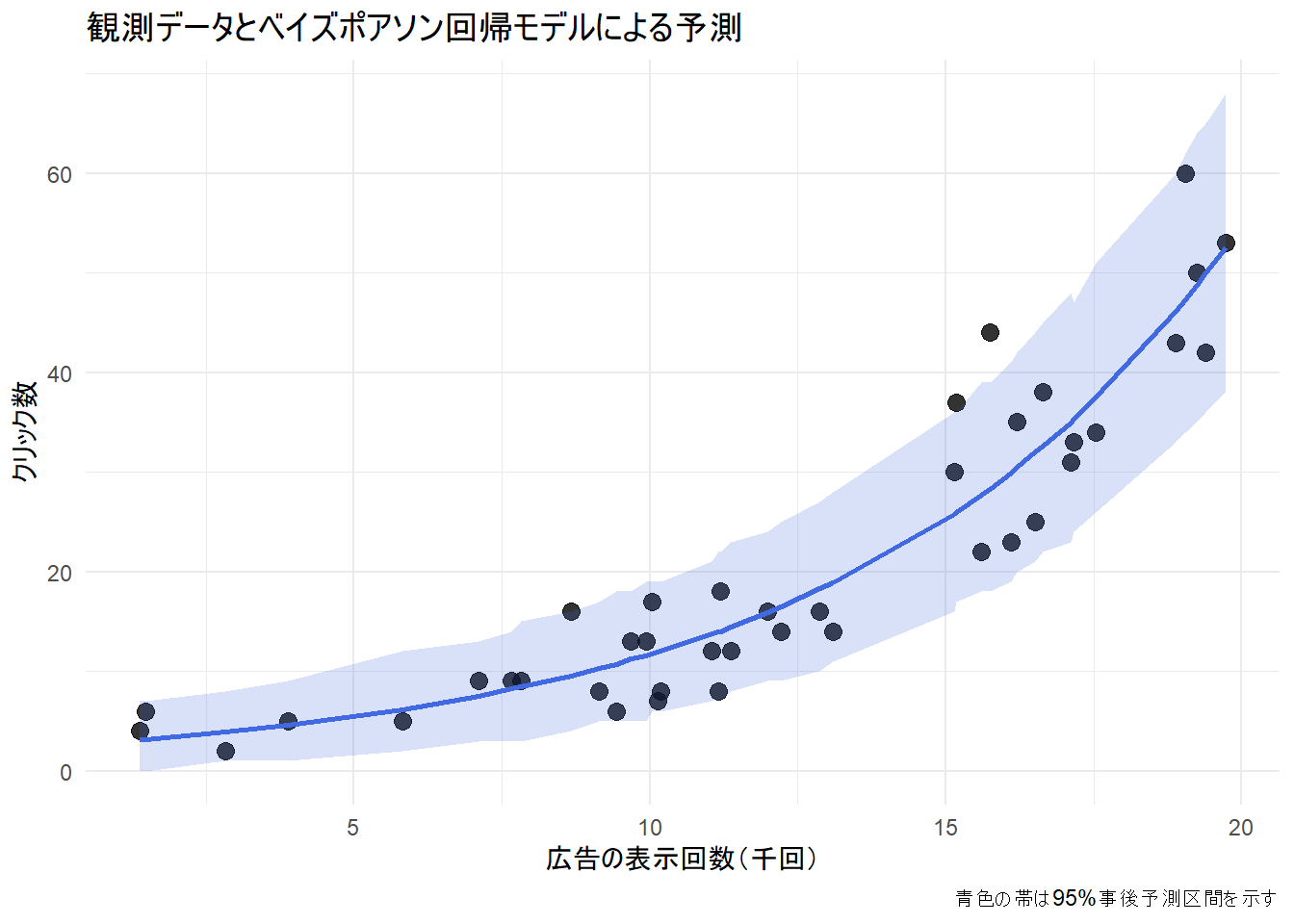
title = "観測データとベイズポアソン回帰モデルによる予測",
x = "広告の表示回数(千回)",
y = "クリック数",
caption = "青色の帯は95%事後予測区間を示す"
) +
theme_minimal(base_family = "sans")
print(prediction_plot)1. 黒色の点 (観測データ)
- シミュレーションで作成した実際のデータ点です。横軸が「広告の表示回数」、縦軸がそのときの「クリック数」を示しています。この散布図が、モデルが説明しようとしている現実そのものです。
2. 青色の実線 (平均予測)
- 各「広告の表示回数」の値に対してモデルが予測するクリック数の平均値を繋いだ線であり、モデルの事後分布に含まれる多数のパラメータセットを用いて予測を行い、それらを平均化したものです。それゆえ、モデルによる「最も確からしい」予測のトレンドを示しています。
- 線が直線ではなく曲線を描いているのは、このモデルが対数(log)リンク関数を持つポアソン回帰モデルであるためです。表示回数が増えるにつれて、クリック数が指数関数的に増加していく関係性を捉えています。
3. 青色の帯 (95%事後予測区間)
「ある表示回数が与えられたとき、次に観測されるであろう新しいデータ点1つが、95%の確率でこの帯の範囲内に収まるだろう」というモデルの予測を示しています。
予測区間の意味
この区間の幅は、モデルが持つ2種類の不確実性を両方とも反映しています。
パラメータの不確実性:
モデルは、切片や係数の「真の値」を完全には知りません。事後分布という形で、その不確実性を保持しています。この不確実性が、予測のぶれの一因となります。
データ固有のばらつき(サンプリングの不確実性):
たとえパラメータが完全にわかっていたとしても、クリック数はポアソン分布に従う確率的な現象であるため、必ずばらつきが生じます。この本質的なランダム性も、予測のぶれに加わります。
青色の帯は、これら2つの不確実性を合算した、総合的な予測の不確かさを表しています。
総合的な解釈
トレンドの的確な把握:
青色の実線は、黒い点(観測データ)の全体的な流れを非常によく追従しています。広告の表示回数が増えるにつれて、クリック数の平均的な予測値も指数関数的に増加する関係性を、モデルは捉えています。
不確実性の適切な評価:
- ほとんど黒い点が、青色の帯(95%事後予測区間)の中に収まっています。これは、モデルが自身の予測の不確実性を適切に見積もれていることを示しています。もし多くの点が帯の外にはみ出していれば、モデルは予測の不確実性を過小評価していることになります。
- 表示回数が増えるほど、予測の不確実性(帯の幅)も増大しています。これは、クリック数の期待値が大きいほど、そのばらつき(分散)も大きくなるというポアソン分布の性質を、モデルが正しく反映している証拠です。
以上です。