Rの関数から tls {tls} を確認します。
tls関数について
tls関数は、Total Least Squares(TLS,以降、本ポストでは「総最小二乗法」と呼称します)を用いて線形回帰モデルの係数を推定するための関数です。
通常の最小二乗法(Ordinary Least Squares, OLS)が、目的変数(Y)にのみ誤差が含まれると仮定するのに対し、総最小二乗法は、目的変数(Y)と説明変数(X)の両方に誤差が含まれる状況を想定しています。
それゆえ、測定誤差を伴う変数間の関係性をより正確にモデル化する際に有用な手法です。
この手法は、幾何学的には、データ点から回帰直線までの直交距離の二乗和を最小化することに相当します。
ソースコードから、tls関数には以下の制約と特徴があることがわかります。
切片なしモデル(原点を通るモデル)専用である:
attr(model, "intercept")をチェックし、切片項が存在する場合はエラーを返します。それゆえ、y ~ xのような式ではなくy ~ x - 1やy ~ 0 + xのような形式でモデルを指定する必要があります。交互作用項は使用できない:
attr(model, "order")をチェックし、交互作用項が含まれている場合はエラーを返します。信頼区間の計算方法を選択できる:
method引数により、正規分布を仮定した方法(“normal”)またはブートストラップ法(“bootstrap”)を選択できます。
tls関数の引数
tls関数は以下の引数を取ります。
library(tls)
args(tls)function (formula, data, method = c("normal", "bootstrap"), conf.level = 0.95,
...)
NULLformula:モデルの構造を定義するformulaオブジェクトです。例えば、
y ~ x1 + x2 - 1のように記述します。注意点として、この関数は切片(intercept)を持つモデルを想定していません。それゆえ、formulaの末尾に- 1を追加するか、0 +を先頭に加えることで、切片が0である(原点を通る)ことを明示的に指定する必要があります。data:モデルで使用する変数を含むデータフレームです。
formulaで指定された変数は、このデータフレームの列名と一致している必要があります。method:回帰係数の信頼区間を計算するための手法を指定する文字列です。デフォルトは
"normal"です。-
"normal": 係数推定量の分布が正規分布に従うと仮定して信頼区間を計算します。 -
"bootstrap": ブートストラップ法を用いて、リサンプリングに基づき信頼区間の経験的分布を求めます。
-
conf.level:信頼区間の信頼水準を指定する、0から1の間の数値です。デフォルトは
0.95であり、95%信頼区間が計算されます。...:将来的な拡張などのために予約されている引数です。現在のバージョンでは、この引数に値を渡しても関数の動作に影響はありません。
シミュレーション
tls関数を確認するため、説明変数と目的変数の両方に測定誤差が含まれる状況をシミュレーションで再現し、通常の最小二乗法(lm関数)の結果と比較します。
サンプルデータの作成
シミュレーションの前提として、まず誤差を含まない「真の」関係性を設定します。ここでは、真の関係が y_true = 2 * x_true であると仮定します。
次に、この真の値に対して、それぞれ正規分布に従う誤差(ノイズ)を加え、観測データ x_obs と y_obs を生成します。
このデータは、説明変数と目的変数の両方に誤差が含まれる状況を模したものです。それゆえ、tls関数の適用対象として適切です。
Rコードによるシミュレーション
以下に、サンプルデータの作成からtls関数の実行、そして結果の可視化までを行うRコードを示します。
# 再現性のために乱数のシードを固定
seed <- 20251112
set.seed(seed)
# 1. サンプルデータの作成
# 真のデータ点の数
n <- 100
# 真の説明変数 (誤差を含まない)
# 1から10の範囲で一様分布に従う乱数を生成します
x_true <- runif(n, 1, 10)
# 真の関係を定義 (y = 2x)
# この傾き「2」が、推定したい真のパラメータです
true_slope <- 2
y_true <- true_slope * x_true
# 測定誤差を生成
# 説明変数(X)と目的変数(Y)の両方に平均0の正規分布に従う誤差を加えます
error_x <- rnorm(n, mean = 0, sd = 1.5)
error_y <- rnorm(n, mean = 0, sd = 1.5)
# 観測データ (測定誤差を含む)
x_obs <- x_true + error_x
y_obs <- y_true + error_y
# データフレームを作成
sim_data <- data.frame(x_obs, y_obs)
cat("--- 作成したサンプルデータの一部を確認 ---\n")
print(str(sim_data))--- 作成したサンプルデータの一部を確認 ---
'data.frame': 100 obs. of 2 variables:
$ x_obs: num 2.04 2.6 2.07 5.8 7.97 ...
$ y_obs: num 8.18 6.65 4.39 7.77 18.06 ...
NULL# 2. tls関数によるパラメータ推定
# method = "normal" を用いて総最小二乗法を実行します
# formulaでは切片を0にするため "- 1" を指定します
tls_fit_normal <- tls(y_obs ~ x_obs - 1, data = sim_data, method = "normal")
# method = "bootstrap" を用いて総最小二乗法を実行します
# こちらも同様に切片を0に指定します
tls_fit_bootstrap <- tls(y_obs ~ x_obs - 1, data = sim_data, method = "bootstrap")
# 3. 比較のための通常最小二乗法(lm)によるパラメータ推定
# lm関数でも同様に切片を0に指定して実行します
lm_fit <- lm(y_obs ~ x_obs - 1, data = sim_data)
# 4. 結果の表示
cat("--- 推定結果の比較 ---\n\n")
cat("総最小二乗法 (TLS, method='normal') の結果:\n")
print(tls_fit_normal)
cat("\n")
cat("総最小二乗法 (TLS, method='bootstrap') の結果:\n")
print(tls_fit_bootstrap)
cat("\n")
cat("通常最小二乗法 (OLS) の結果:\n")
# lmの結果から係数と信頼区間を抽出して表示します
lm_coef <- coef(lm_fit)
lm_confint <- confint(lm_fit)
cat("係数 (x_obs):", lm_coef, "\n")
cat("信頼区間:\n")
print(lm_confint)
cat("\n")
cat("--- 結果の要約 ---\n")
cat(sprintf("真の傾き: %.4f\n", true_slope))
cat(sprintf("TLS (normal) による傾きの推定値: %.4f\n", tls_fit_normal$coefficient))
cat(sprintf("TLS (bootstrap) による傾きの推定値: %.4f\n", tls_fit_bootstrap$coefficient))
cat(sprintf("OLS (lm) による傾きの推定値: %.4f\n\n", lm_coef))--- 推定結果の比較 ---
総最小二乗法 (TLS, method='normal') の結果:
$coefficient
[1] 2.003322
$confidence.interval
2.5% lower bound 97.5% upper bound
[1,] 1.897571 2.109073
$sd.est
[1] 0.05395556
総最小二乗法 (TLS, method='bootstrap') の結果:
$coefficient
[1] 2.003322
$confidence.interval
2.5% lower bound 97.5% upper bound
[1,] 1.889746 2.130656
$sd.est
[,1]
[1,] 0.06188964
通常最小二乗法 (OLS) の結果:
係数 (x_obs): 1.894552
信頼区間:
2.5 % 97.5 %
x_obs 1.792795 1.996309
--- 結果の要約 ---
真の傾き: 2.0000
TLS (normal) による傾きの推定値: 2.0033
TLS (bootstrap) による傾きの推定値: 2.0033
OLS (lm) による傾きの推定値: 1.8946TLS (normal / bootstrap) による傾きの推定値: 2.0033
総最小二乗法(TLS)によって推定された傾きです。この値は真の傾きである
2.0000に近く、誤差は約0.17%です。method引数を"normal"と"bootstrap"のどちらに設定しても、同じ推定値が得られています。この結果は、TLSが説明変数と目的変数の両方に含まれる誤差を考慮し、推定を行っていることを示しています。OLS (lm) による傾きの推定値: 1.8946
通常最小二乗法(OLS)、すなわちRの
lm関数によって推定された傾きです。この値は真の傾き2.0000と比較して小さくなっており、約5.3%の過小評価となっています。
# 5. 結果の可視化
# 描画領域を設定
plot(sim_data$x_obs, sim_data$y_obs,
main = "総最小二乗法(TLS)と通常最小二乗法(OLS)の比較",
xlab = "説明変数 (観測値 x_obs)",
ylab = "目的変数 (観測値 y_obs)",
pch = 16, col = "gray",
cex.main = 1.5, cex.lab = 1.2
)
# 真の関係を示す直線 (y = 2x) を破線で描画
abline(a = 0, b = true_slope, col = "red", lty = 2, lwd = 5.5)
# TLSによる回帰直線を青色で描画
abline(a = 0, b = tls_fit_normal$coefficient, col = "blue", lty = 1, lwd = 2.5)
# OLSによる回帰直線を緑色で描画
abline(a = 0, b = lm_coef, col = "darkgreen", lty = 1, lwd = 2.5)
# 凡例を追加
legend("topleft",
legend = c("観測データ点", "真の関係 (y = 2x)", "TLSによる回帰直線", "OLSによる回帰直線"),
col = c("gray", "red", "blue", "darkgreen"),
lty = c(NA, 2, 1, 1),
pch = c(16, NA, NA, NA),
lwd = 2,
bg = "white"
)観測データ点(灰色の点):
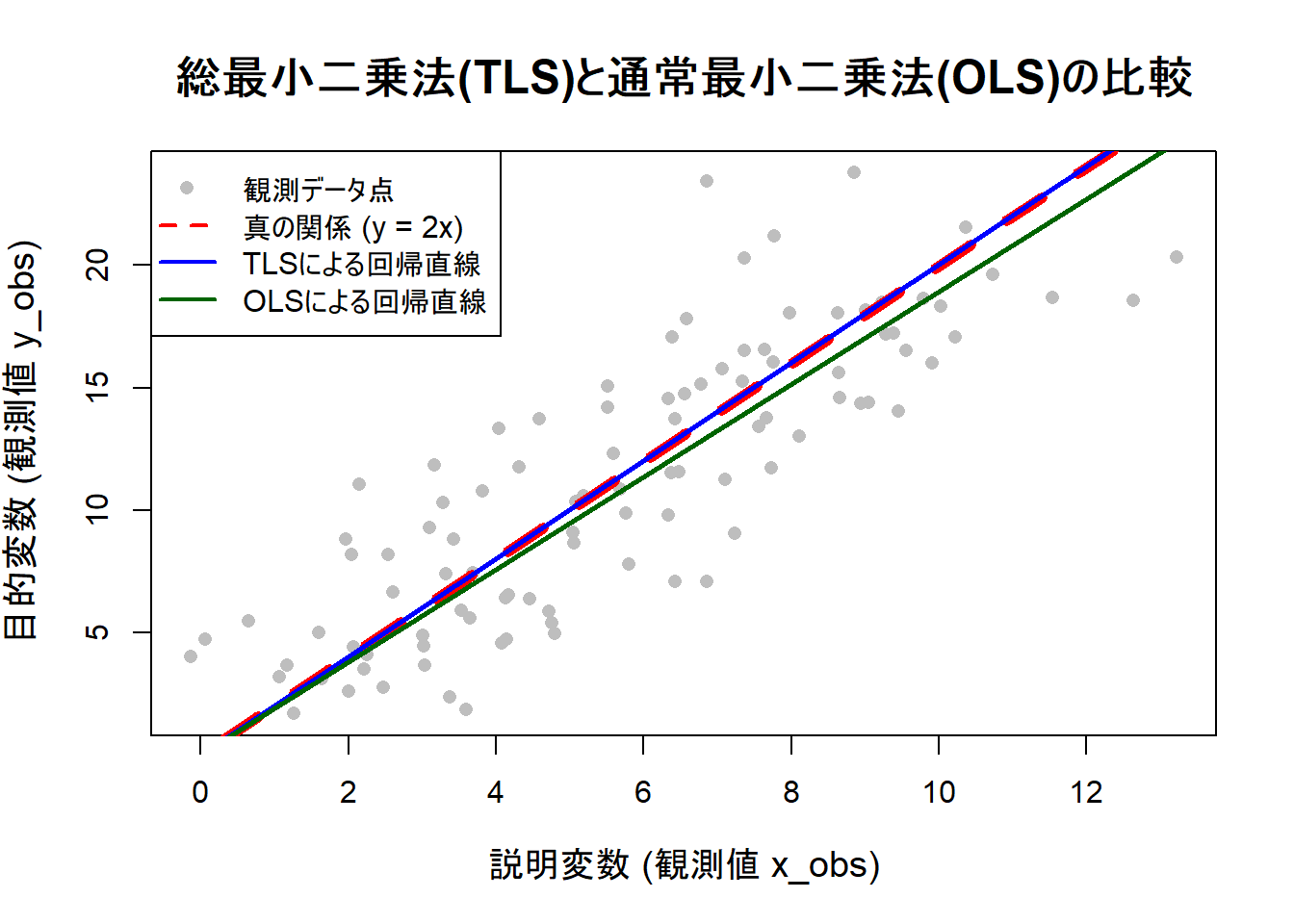
シミュレーションで生成された、測定誤差を含む個々のデータ点です。これらの点は、これから推定しようとする「真の関係」を示す直線の周囲に、ある程度のばらつきを持って分布しています。
真の関係 (y = 2x)(赤色の破線):
データが本来従うべき、誤差が一切含まれない理想的な関係(傾きが
2の原点を通る直線)です。回帰分析の目標は、灰色のデータ点の集まりから、この赤色の破線を可能な限り正確に推定することです。OLSによる回帰直線(緑色の実線):
通常最小二乗法(OLS)によって推定された回帰直線です。OLSは、各データ点から回帰直線への「垂直方向の距離」の合計が最小になるように直線を引きます。Figure 1 では、緑色の直線は赤色の破線よりも傾きが緩やか(小さく)なっています。これは、OLSが説明変数(X軸方向)の誤差を考慮しないため、係数を過小評価してしまっていることを示しています。
TLSによる回帰直線(青色の実線):
総最小二乗法(TLS)によって推定された回帰直線です。TLSは、各データ点から回帰直線への「直交距離(最も短い距離)」の合計が最小になるように直線を引きます。それゆえ、X軸とY軸両方の誤差を考慮した推定が可能です。Figure 1 が示す通り、青色の直線は赤色の破線とほぼ重なっており、TLSが真の関係を捉えていることがわかります。
切片を含めたモデル
# formula内で行列を生成し、切片(1)を含めてtls関数を実行
# このコードはエラーを引き起こします
result <- tryCatch(
{
tls(y_obs ~ cbind(1, x_obs), data = sim_data)
},
error = function(e) {
# 発生したエラーメッセージを表示
cat("--- エラーメッセージの確認 ---\n")
print(e$message)
}
)--- エラーメッセージの確認 ---
[1] "Using total least squares requires model without intercept."切片項無しのモデルとする必要がある、とのエラーメッセージが出力されます。
以上です。