Rの関数から zeroinfl {pscl} を確認します。
本ポストはこちらの続きです。

zeroinfl関数とは
zeroinfl(ゼロ過剰)モデルは、hurdleモデルと同様に、ゼロが非常に多く観測されるカウントデータ(ゼロ過剰データ)を分析するための統計モデルです。
hurdleモデルがデータの生成プロセスを「ゼロか正の値か」の2段階で考えるのに対し、zeroinflモデルはデータを2つの異なるグループが混合したものとして捉えます。
- 常時ゼロ群 (Always-Zero Group):
- このグループに属する観測は、構造的に必ずゼロになります。例えば、「特定の医薬品の副作用を報告する」という調査において、そもそもその医薬品を処方されていない患者は、副作用を報告する可能性が構造的にゼロです。このような「ありえない」ゼロを構造的ゼロ (Structural Zeros)と呼びます。
zeroinflモデルでは、観測値がこのグループに属する確率を二項モデル(ロジスティック回帰など)でモデル化します。
- このグループに属する観測は、構造的に必ずゼロになります。例えば、「特定の医薬品の副作用を報告する」という調査において、そもそもその医薬品を処方されていない患者は、副作用を報告する可能性が構造的にゼロです。このような「ありえない」ゼロを構造的ゼロ (Structural Zeros)と呼びます。
- カウント過程群 (Count Process Group):
- こちらのグループに属する観測は、通常のカウントデータ生成プロセス(ポアソン分布や負の二項分布など)に従います。重要なのは、こちらのグループからも偶然ゼロが生成される可能性があるという点です。例えば、医薬品を処方された患者でも、たまたま副作用が出なかった場合のゼロがこれにあたります。このようなゼロはサンプリングゼロ (Sampling Zeros)と呼ばれます。
つまり、zeroinflモデルは、観測された多数のゼロを「構造的ゼロ」と「サンプリングゼロ」の混合として分解し、それぞれに影響を与える要因を同時に推定するモデルです。
zeroinfl関数とhurdle関数の違い
-
hurdleモデル:- 「ゼロ」と「正の値」を明確に分離します。正の値のカウントプロセスからは、ゼロは生成されません。
-
zeroinflモデル:- 「常にゼロである状態」と「カウントが発生しうる状態(ただし結果がゼロになることもある)」を混合します。
どちらのモデルが適切かは、対象とするデータの背景や、ゼロが生まれるメカニズムをどのように解釈するかによって決まります。
zeroinfl関数の引数
以下にzeroinfl関数の引数について確認します。引数の多くはhurdle関数と共通しています。
library(pscl)
args(zeroinfl)function (formula, data, subset, na.action, weights, offset,
dist = c("poisson", "negbin", "geometric"), link = c("logit",
"probit", "cloglog", "cauchit", "log"), control = zeroinfl.control(...),
model = TRUE, y = TRUE, x = FALSE, ...)
NULL-
formula- モデルの構造を定義する式。
y ~ x1 + x2 | z1 + z2のように、|の左側にカウント過程部分のモデル式を、右側にゼロ過剰部分(常時ゼロ群に属する確率)のモデル式を記述します。
- モデルの構造を定義する式。
-
data- モデルに使用するデータフレーム。
-
subset,na.action,weights,offset- それぞれ、サブセット指定、欠損値処理、重み、オフセット項を指定する、
hurdle関数と共通の引数です。
- それぞれ、サブセット指定、欠損値処理、重み、オフセット項を指定する、
-
dist- カウント過程部分の確率分布を指定します。選択肢は
"poisson"(ポアソン分布),"negbin"(負の二項分布),"geometric"(幾何分布) です。デフォルトは"poisson"です。
- カウント過程部分の確率分布を指定します。選択肢は
-
link- ゼロ過剰部分の二項モデルにおけるリンク関数です。選択肢は
"logit","probit","cloglog","cauchit","log"です。デフォルトは"logit"で、ロジスティック回帰を意味します。
- ゼロ過剰部分の二項モデルにおけるリンク関数です。選択肢は
-
control-
optim関数による最適化の際の詳細な設定を行うためのリスト。
-
-
model,y,x- 結果のオブジェクトに、それぞれモデルフレーム、応答変数、計画行列を含めるかどうかを指定する論理値。
シミュレーション
それでは、zeroinfl関数を確認するためのシミュレーションを行います。
ここでは、「ある専門的なソフトウェアの、1ヶ月あたりの有料プラグイン購入数」を想定したサンプルデータを作成します。
ユーザーの中には、そもそもそのソフトウェアのライセンスが無料版であるためプラグインを購入できない層(構造的ゼロ)と、有料ライセンスを持っていて購入は可能だが、結果的に購入しない月もある層(サンプリングゼロの可能性)が存在する、という状況を考えます。
なお、有意水準は5%とします。
1. 準備
シミュレーションに必要なパッケージを読み込みます。
library(ggplot2)
library(dplyr)2. サンプルデータの作成
ゼロ過剰(Zero-Inflated)なサンプルデータを生成します。
-
z1(ユーザーのステータスが学生か) とz2(無料版ライセンスか) が、プラグインを購入できない「常時ゼロ群」に属する確率に影響を与えるとします。 -
x1(ソフトウェアの利用頻度) とx2(ユーザーの経験年数) が、「カウント過程群」に属する場合のプラグイン購入数に影響を与えるとします。
seed <- 20251104
set.seed(seed)
n <- 2000 # サンプルサイズ
# 説明変数の生成
z1 <- rbinom(n, 1, 0.3) # ゼロ過剰部分: 学生か (1 = 学生)
z2 <- rbinom(n, 1, 0.4) # ゼロ過剰部分: 無料版ライセンスか (1 = 無料版)
x1 <- rnorm(n, mean = 10, sd = 3) # カウント部分: ソフトウェア利用頻度
x2 <- runif(n, 0, 8) # カウント部分: ユーザーの経験年数
# --- ゼロ過剰部分のモデル化 ---
# 学生(z1)であったり無料版(z2)であったりすると、「常時ゼロ群」に属する確率が高まると仮定
# ロジットリンク関数の逆関数 plogis() を用いて確率を計算
# 係数を設定: intercept=-1.5, z1=1.0, z2=2.5
prob_structural_zero <- plogis(-1.5 + 1.0 * z1 + 2.5 * z2)
# 上記の確率に基づき、二項分布から常時ゼロ群(1)かカウント過程群(0)かを生成
is_structural_zero <- rbinom(n, 1, prob_structural_zero)
# --- カウント部分のモデル化 ---
# 利用頻度が高く(x1)、経験年数が長い(x2)ほど、購入数が多くなると仮定
# ログリンク関数なので、exp() を用いてポアソン分布の期待値(ラムダ)を計算
# 係数を設定: intercept=-1.0, x1=0.15, x2=0.1
lambda <- exp(-1.0 + 0.15 * x1 + 0.1 * x2)
# カウント過程群の購入数をポアソン分布から生成(この中にはゼロも含まれうる)
count_process_y <- rpois(n, lambda)
# --- 最終的な目的変数の作成 ---
# is_structural_zeroが1の場合は0、0の場合はcount_process_yの値を採用
y <- ifelse(is_structural_zero == 1, 0, count_process_y)
# データフレームの作成
sim_data_zi <- data.frame(y, x1, x2, z1, z2)
# 生成したデータの分布を確認
cat("作成した目的変数 y の要約:\n")
print(summary(sim_data_zi$y))
cat(sprintf("\nゼロの割合: %.2f%%\n", mean(sim_data_zi$y == 0) * 100))
# データの可視化
ggplot(sim_data_zi, aes(x = y)) +
geom_histogram(binwidth = 1, fill = "darkred", color = "white", alpha = 0.8) +
labs(
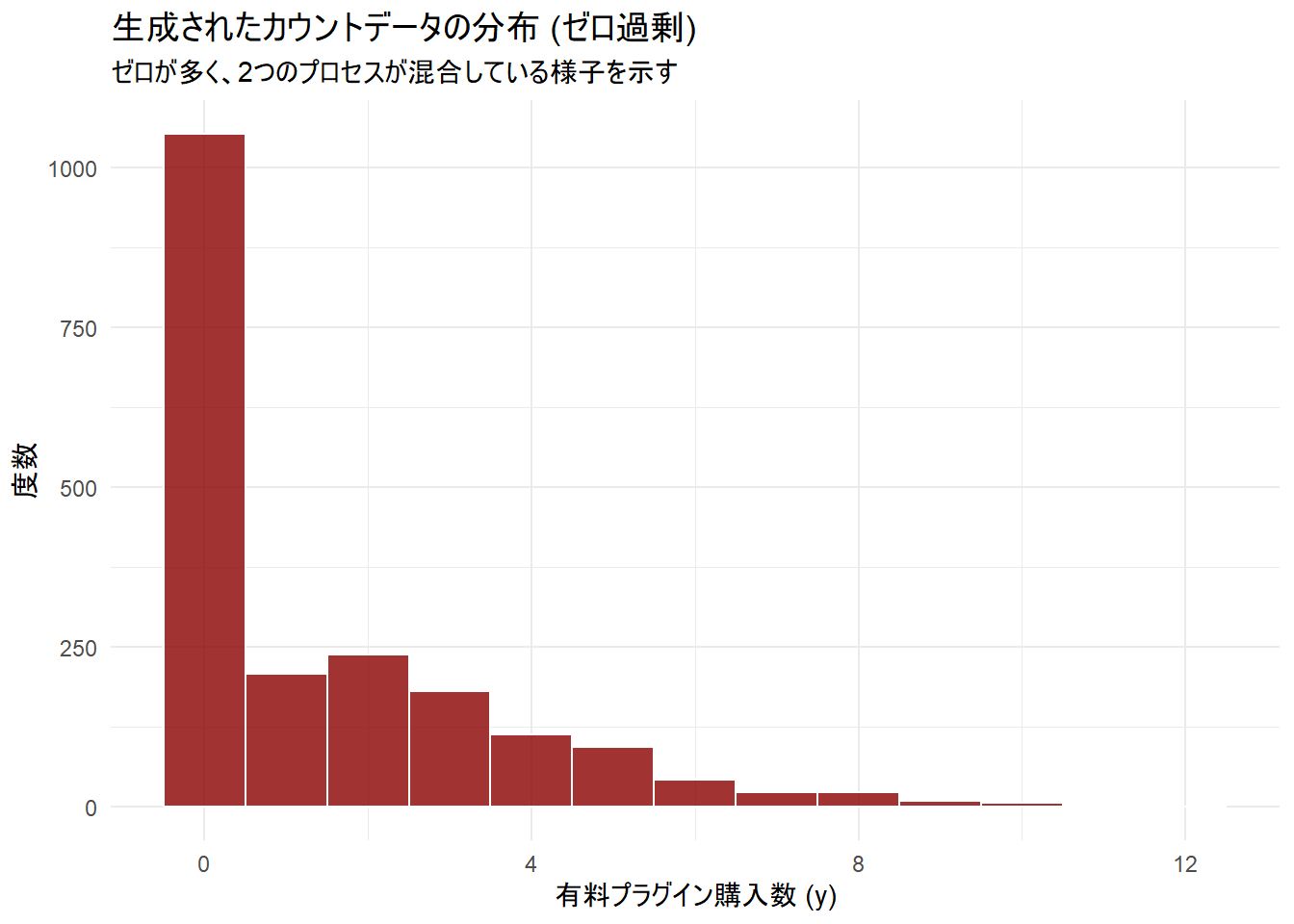
title = "生成されたカウントデータの分布 (ゼロ過剰)",
subtitle = "ゼロが多く、2つのプロセスが混合している様子を示す",
x = "有料プラグイン購入数 (y)",
y = "度数"
) +
theme_minimal()作成した目的変数 y の要約:
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.000 0.000 0.000 1.482 2.250 12.000
ゼロの割合: 52.65%生成されたデータでは、約53%がゼロであり、ゼロが過剰に観測されるデータとなっていることが確認できます。
3. zeroinflモデルの適用
作成したサンプルデータに対してzeroinflモデルを適用します。データ生成の際に仮定した通り、カウント部分のモデルにはx1とx2を、ゼロ過剰部分のモデルにはz1とz2を使用します。
# ゼロ過剰モデルの推定
# カウント部分はポアソン分布(dist = "poisson")
# ゼロ過剰部分は二項分布(link = "logit")
zeroinfl_model <- zeroinfl(
y ~ x1 + x2 | z1 + z2,
data = sim_data_zi,
dist = "poisson",
link = "logit"
)4. 結果の確認
モデルの推定結果をsummary()で確認します。
cat("ゼロ過剰モデルの推定結果:\n")
summary(zeroinfl_model)ゼロ過剰モデルの推定結果:
Call:
zeroinfl(formula = y ~ x1 + x2 | z1 + z2, data = sim_data_zi, dist = "poisson", link = "logit")
Pearson residuals:
Min 1Q Median 3Q Max
-1.5134 -0.5378 -0.3049 0.5200 6.6206
Count model coefficients (poisson with log link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.995835 0.091051 -10.94 <2e-16 ***
x1 0.147816 0.006716 22.01 <2e-16 ***
x2 0.102800 0.008706 11.81 <2e-16 ***
Zero-inflation model coefficients (binomial with logit link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.4250 0.1049 -13.590 < 2e-16 ***
z1 1.0955 0.1348 8.125 4.49e-16 ***
z2 2.4427 0.1319 18.520 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Number of iterations in BFGS optimization: 12
Log-likelihood: -2729 on 6 Df全体のサマリー
Call:
zeroinfl(formula = y ~ x1 + x2 | z1 + z2, data = sim_data_zi, dist = "poisson", link = "logit")このCallセクションは、このモデルがどのような設定で実行されたかを示しています。
-
formula = y ~ x1 + x2 | z1 + z2: 目的変数yに対し、|の左側 (x1 + x2) がカウント過程部分を、右側 (z1 + z2) がゼロ過剰部分をモデル化するために使用されたことを意味します。 -
dist = "poisson": カウント過程部分(プラグイン購入が発生しうる場合)の購入数が、ポアソン分布に従うと仮定されています。 -
link = "logit": ゼロ過剰部分(構造的に購入数がゼロになるかどうか)が、ロジットリンク関数を用いた二項分布(ロジスティック回帰)でモデル化されていることを示します。
1. カウントモデル部分 (Count model coefficients)
Count model coefficients (poisson with log link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.995835 0.091051 -10.94 <2e-16 ***
x1 0.147816 0.006716 22.01 <2e-16 ***
x2 0.102800 0.008706 11.81 <2e-16 ***こちらのパートは、「もしユーザーがプラグインを購入する可能性があるグループ(カウント過程群)に属している場合、その購入数が何に影響されるか」を分析した結果です。
- 解釈:
-
(Intercept): 切片です。x1とx2が共に0のときの、対数スケールでの平均購入数に相当します。 -
x1(ソフトウェア利用頻度): 係数(Estimate)は0.147816と正の値です。利用頻度が高いユーザーほど、購入数が多くなる傾向にあることを示しています。 -
x2(ユーザーの経験年数): 係数は0.102800とこちらも正の値です。経験年数が長いユーザーほど、購入数が多くなることを示唆しています。
-
- 統計的有意性:
-
Pr(>|z|)列のp値は、全ての変数で2e-16より小さい(ほぼ0に近い)値と、設定した有意水準を下回っており、これらの変数が購入数に与える影響は有意であることを意味します。 - この結果は、データ生成時の設定(
x1の係数=0.15,x2の係数=0.1)をモデルが推定できていることを裏付けています。
-
2. ゼロ過剰モデル部分 (Zero-inflation model coefficients)
Zero-inflation model coefficients (binomial with logit link):
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.4250 0.1049 -13.590 < 2e-16 ***
z1 1.0955 0.1348 8.125 4.49e-16 ***
z2 2.4427 0.1319 18.520 < 2e-16 ***こちらのパートは、「そもそもユーザーが構造的に購入できないグループ(常時ゼロ群)に属する確率が何に影響されるか」を分析した結果です。
- 解釈:
-
(Intercept): 切片です。z1とz2が共に0のときの、「常時ゼロ群」に属する確率の対数オッズです。 -
z1(学生か): 係数は1.0955と正の値です。学生であるユーザーは、「常時ゼロ群」に属する確率、すなわち構造的に購入数がゼロとなる確率が高いことを示しています。 -
z2(無料版ライセンスか): 係数は2.4427と正の値です。無料版ライセンスのユーザーは、「常時ゼロ群」に属する確率が高いことを示唆しています。
-
- 統計的有意性:
- カウントモデル部分と同様に、p値は設定した有意水準を下回っており、全ての変数が有意であることが示されています。
- この結果も、データ生成時の設定(
z1の係数=1.0,z2の係数=2.5)をモデルが推定できていることを示しています。
補足情報
-
Pearson residuals: モデルの当てはまりを診断するための残差の要約統計量です。 -
Number of iterations in BFGS optimization: 12: モデルパラメータを推定するための計算(最適化)が12回の反復で収束したことを示します。少ない回数での収束は、推定が問題なく完了したことを意味します。 -
Log-likelihood: -2729 on 6 Df: モデルの対数尤度です。モデルの適合度を示す指標で、6 Dfはモデルが6個のパラメータ(カウント部分で3個、ゼロ過剰部分で3個)を推定したことを示します。
5. 予測と可視化
構築したモデルを用いて予測値と実測値を比較し、モデルの当てはまりを視覚的に確認します。
# 予測値の取得
sim_data_zi$predicted <- predict(zeroinfl_model, type = "response")
# 実測値と予測値の比較プロット
ggplot(sim_data_zi, aes(x = predicted, y = y)) +
geom_jitter(alpha = 0.2, width = 0.2, height = 0.2, color = "darkred") +
geom_abline(intercept = 0, slope = 1, color = "blue", linetype = "dashed", size = 1) +
labs(
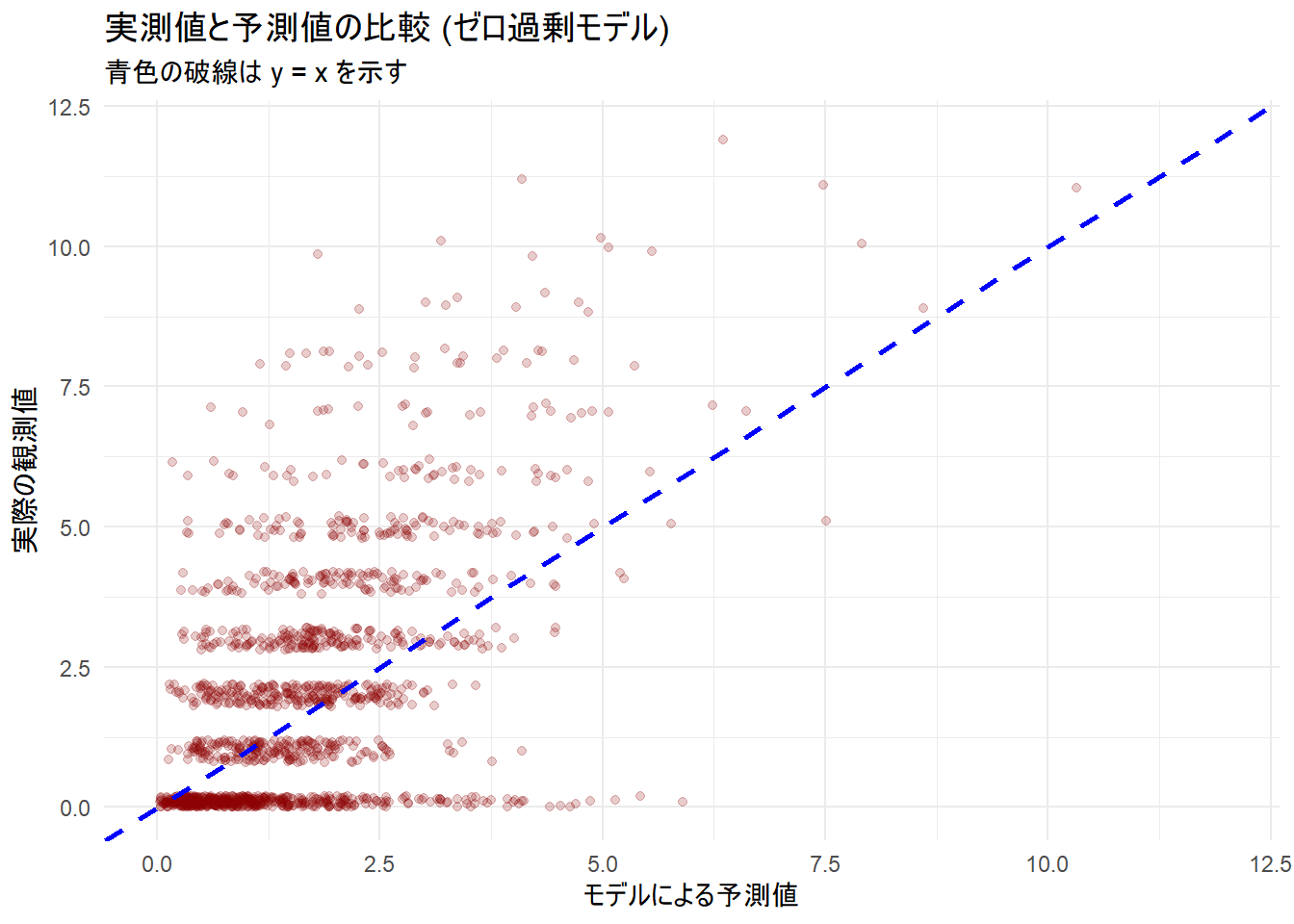
title = "実測値と予測値の比較 (ゼロ過剰モデル)",
subtitle = "青色の破線は y = x を示す",
x = "モデルによる予測値",
y = "実際の観測値"
) +
xlim(0, max(sim_data_zi$predicted, sim_data_zi$y)) +
ylim(0, max(sim_data_zi$predicted, sim_data_zi$y)) +
theme_minimal()以上です。