Rの関数:nnet {nnet}

Rの関数から nnet {nnet} を確認します。

本ポストはこちらの続きです。

Rの関数nnet.defaultとstats::glmの等価性の確認

Rの関数 nnet.default と stats::glm の等価性を確認します本ポストはこちらの続きです。nnet.default と glm の等価性の確認nnetパッケージの基幹関数 nnet.default を特定の引数（size...

関数 `nnet` とは

nnet は、バックプロパゲーション（誤差逆伝播法）に類似した最適化手法（BFGS法など）を用いて、入力層から隠れ層を経て出力層に至るネットワークの重みを学習します。回帰問題と分類問題の双方に対応可能です。

関数 `nnet` の引数

library(nnet)
methods(nnet)

[1] nnet.default nnet.formula
see '?methods' for accessing help and source code

args(getS3method("nnet", "default"))

function (x, y, weights, size, Wts, mask = rep(TRUE, length(wts)), 
    linout = FALSE, entropy = FALSE, softmax = FALSE, censored = FALSE, 
    skip = FALSE, rang = 0.7, decay = 0, maxit = 100, Hess = FALSE, 
    trace = TRUE, MaxNWts = 1000, abstol = 1e-04, reltol = 1e-08, 
    ...) 
NULL

x
- 入力データ行列。説明変数が格納された行列またはデータフレームです。欠損値（NA）を含むことはできません。
y
- 教師データ行列。目的変数が格納された行列です。回帰の場合は数値、分類の場合はクラスを示す指標行列（ダミー変数化されたものなど）を用います。x と行数が一致する必要があります。
weights
- 重みベクトル。各データポイント（観測値）に対する重要度を指定します。指定しない場合、すべての観測値の重みは1となります。
size
- 隠れ層のユニット数。ニューラルネットワークの複雑さを決定するパラメータです。0の場合は隠れ層なし（ロジスティック回帰や線形回帰と同等）となります。
Wts
- 初期重みベクトル。最適化の開始点となる重みを指定する場合に使用します。省略時は乱数により初期化されます。
mask
- 学習対象の重みを指定する論理ベクトル。TRUE の位置にある重みのみが更新され、FALSE の位置は固定されます。特定の結合を無効化する際に有用です。
linout
- 線形出力の有無。TRUE に設定すると出力ユニットの活性化関数が線形関数（恒等関数）となり、回帰問題に適した設定となります。デフォルト（FALSE）はロジスティック関数です。
entropy
- 交差エントロピー誤差の利用。TRUE の場合、学習時の損失関数として、二乗誤差の代わりに（最大条件付き尤度に基づく）エントロピーを使用します。主にロジスティック出力の場合に使用されます。
softmax
- ソフトマックス関数の利用。TRUE の場合、出力層にソフトマックス関数を適用します。これにより出力の総和が1となり、確率として解釈可能になるため、多クラス分類に利用される設定です。
censored
- 打ち切りデータの扱い。TRUE の場合、生存時間解析のような打ち切りデータを扱うためのバリアントとして動作します。
skip
- スキップ接続の追加。TRUE の場合、入力層から出力層へ直接つながる結合（隠れ層をバイパスする経路）を追加します。線形モデルで説明できる部分を保持しつつ、非線形性を隠れ層で補う構造になります。
rang
- 初期重みの範囲。初期重みを生成する際の一様乱数の範囲 [-rang, rang] を指定します。
decay
- 重み減衰（Weight Decay）パラメータ。過学習を防ぐための正則化項です。重みの二乗和に比例したペナルティを誤差関数に加えます。この値が大きいほどモデルは単純化されます。
maxit
- 最大反復回数。最適化計算を行う最大ステップ数です。
Hess
- ヘッセ行列の計算。TRUE の場合、最適化終了後にヘッセ行列（目的関数の二階微分行列）を計算して返します。信頼区間の推定などに用いられます。
trace
- 経過の表示。TRUE の場合、最適化の各段階における誤差の値をコンソールに出力します。
MaxNWts
- 重みの最大許容数。ネットワークが大きくなりすぎて計算不能になるのを防ぐための安全対策です。デフォルトは1000です。
abstol
- 絶対許容誤差。最適化の収束判定基準の一つです。
reltol
- 相対許容誤差。最適化の収束判定基準の一つです。
…
- その他の引数。将来的な拡張や内部関数へのパススルー用です。

シミュレーション用サンプルデータの作成と実装

関数 nnet の挙動のうち、「回帰」と「多クラス分類」という2つの側面を確認するためのサンプルデータを作成します。

回帰問題用データ:
非線形な関係（正弦波にノイズを加えたもの）を持つデータ。linout = TRUE の効果を確認します。
分類問題用データ:
線形分離不可能な3つのクラス（同心円状の分布）を持つデータ。softmax = TRUE と size（隠れ層）の効果を確認します。

以下は、サンプルデータ生成からモデル構築、可視化までを行うRコードです。

# 乱数シードの固定（再現性のため）
seed <- 20251122

シミュレーション1: 回帰問題 (非線形関数の近似)

通常、ニューラルネットワークの出力層にはロジスティック関数（0から1の範囲）が用いられますが、回帰分析において目的変数 \(Y\) がその範囲外を取る場合、適切な予測が行えません。

そこで、linout = TRUE とすることで、出力層が恒等関数となり、任意の実数値を予測できるようになります。

set.seed(seed)

# 1. サンプルデータの作成
# 説明変数 x: 0から10までの範囲で等間隔に生成
x_reg <- seq(0, 10, length.out = 100)
# 目的変数 y: xに対してsin関数を適用し、正規乱数のノイズを加える
y_true <- sin(x_reg)
y_noise <- y_true + rnorm(length(x_reg), mean = 0, sd = 0.2)

# nnet.defaultに渡すため行列形式に変換
x_reg_mat <- as.matrix(x_reg)
y_reg_mat <- as.matrix(y_noise)

# 2. nnetによるモデル構築 (回帰設定)
# size=10: 隠れ層のニューロン数を10に設定（複雑な曲線を表現するため）
# linout=TRUE: 出力層を線形関数にする（回帰には必須）
# decay=0.001: 過学習抑制のための重み減衰
# maxit=500: 収束するまで十分に繰り返す
# trace=FALSE: 途中経過の出力を抑制
nn_reg <- nnet(
  x = x_reg_mat,
  y = y_reg_mat,
  size = 10,
  linout = TRUE,
  decay = 0.001,
  maxit = 500,
  trace = FALSE
)

# 3. 予測値の算出
pred_reg <- predict(nn_reg, x_reg_mat)

# 4. 構築したモデルの確認
cat("--- 構築したモデルの確認 ---\n")
print(nn_reg)

--- 構築したモデルの確認 ---
a 1-10-1 network with 31 weights
options were - linear output units  decay=0.001

ネットワーク構造の概要

冒頭の a 1-10-1 network with 31 weights という記述は、モデルのアーキテクチャを表しています。

1-10-1: 各層のニューロン（ユニット）数を示しています。
- 入力層: 1ユニット。説明変数 \(x\) が1つであるため。
- 隠れ層: 10ユニット。引数 size = 10 で指定した値。
- 出力層: 1ユニット。目的変数 \(y\) が1つであるため。
31 weights: 学習対象となったパラメータの総数です。内訳は以下の通りです。
- 入力層 \(\to\) 隠れ層の重み: \(1 \times 10 = 10\) 個
- 隠れ層のバイアス: \(10\) 個
- 隠れ層 \(\to\) 出力層の重み: \(10 \times 1 = 10\) 個
- 出力層のバイアス: \(1\) 個
- 合計: \(10 + 10 + 10 + 1 = 31\) 個

モデルのオプション設定

options were - linear output units decay=0.001 の行は、モデルの挙動を決定する設定を確認するものです。

linear output units: 引数 linout = TRUE が適用されています。通常、ニューラルネットワークの出力は0から1の範囲（ロジスティック関数など）に収められますが、ここでは回帰分析を行うために、出力層が恒等関数（線形）になっており、任意の実数値を出力できる状態であることを示しています。
decay=0.001: 引数 decay = 0.001 が適用されています。重みの値が極端に大きくなることを防ぐ「重み減衰（Weight Decay）」が機能しており、過学習（オーバーフィッティング）が抑制されています。

シミュレーション2: 分類問題 (同心円状の多クラス分類)

set.seed(seed)

# 1. サンプルデータの作成
# サンプル数
n_class <- 100
# 角度をランダムに生成
theta <- runif(n_class * 3, 0, 2 * pi)

# 半径をクラスごとに変えて生成 (中心からの距離でクラス分け)
# クラス1: 半径 0 ~ 2
r1 <- runif(n_class, 0, 2)
# クラス2: 半径 3 ~ 5
r2 <- runif(n_class, 3, 5)
# クラス3: 半径 6 ~ 8
r3 <- runif(n_class, 6, 8)

# 座標 (x1, x2) への変換
x1_c1 <- r1 * cos(theta[1:n_class])
x2_c1 <- r1 * sin(theta[1:n_class])

x1_c2 <- r2 * cos(theta[(n_class + 1):(2 * n_class)])
x2_c2 <- r2 * sin(theta[(n_class + 1):(2 * n_class)])

x1_c3 <- r3 * cos(theta[(2 * n_class + 1):(3 * n_class)])
x2_c3 <- r3 * sin(theta[(2 * n_class + 1):(3 * n_class)])

# データフレームに結合
df_cls <- data.frame(
  x1 = c(x1_c1, x1_c2, x1_c3),
  x2 = c(x2_c1, x2_c2, x2_c3),
  class = factor(rep(c("中心", "中間", "外側"), each = n_class))
)

# nnet.defaultのために、目的変数を指標行列(ダミー変数)に変換
# class.ind関数はnnetパッケージに含まれるユーティリティです
y_cls_ind <- class.ind(df_cls$class)
x_cls_mat <- as.matrix(df_cls[, c("x1", "x2")])

# 2. nnetによるモデル構築 (分類設定)
# size=8: 隠れ層のニューロン数
# softmax=TRUE: 出力を確率として扱う（多クラス分類に必須）
# decay=0.01: 決定境界を滑らかにするための正則化
nn_cls <- nnet(
  x = x_cls_mat,
  y = y_cls_ind,
  size = 8,
  softmax = TRUE,
  decay = 0.01,
  maxit = 500,
  trace = FALSE
)

# 3. 分類境界を可視化するためのグリッドデータ作成
grid_seq <- seq(-9, 9, length.out = 100)
grid_dat <- expand.grid(x1 = grid_seq, x2 = grid_seq)
# グリッド上の各点についてクラス確率を予測
pred_grid_probs <- predict(nn_cls, as.matrix(grid_dat))
# 最も確率が高いクラスを選択
pred_grid_class <- max.col(pred_grid_probs)

# 4. 構築したモデルの確認
cat("--- 構築したモデルの確認 ---\n")
print(nn_cls)

--- 構築したモデルの確認 ---
a 2-8-3 network with 51 weights
options were - softmax modelling  decay=0.01

ネットワーク構造の概要

冒頭の a 2-8-3 network with 51 weights という記述は、モデルのアーキテクチャを表しています。

2-8-3: 各層のニューロン（ユニット）数を示しています。
- 入力層: 2ユニット。入力データの次元数に対応します。今回のシミュレーションでは、2次元平面上の座標 \((x_1, x_2)\) を特徴量として用いました。それゆえ、入力ユニット数は2となります。
- 隠れ層: 8ユニット。関数 nnet の引数 size = 8 で指定した値です。この8つのニューロンが、入力された座標データを非線形変換し、直線では分離できない「同心円」という境界線を表現するための特徴を抽出します。
- 出力層: 3ユニット。分類すべきクラスの数に対応します。データセットには「中心」「中間」「外側」という3つのカテゴリが存在しました。それゆえ、モデルはこれら3つのクラスそれぞれに対するスコアを出力する必要があります。
51 weights: 学習対象となったパラメータの総数です。内訳は以下の通りです。
- 入力層 \(\to\) 隠れ層の重み: (入力2個 + バイアス1個) \(\times\) 隠れニューロン8個 = \(3 \times 8 = 24\) 個
- 隠れ層 \(\to\) 出力層の重み: (隠れニューロン8個 + バイアス1個) \(\times\) 出力ニューロン3個 = \(9 \times 3 = 27\) 個
- 合計: \(24 + 27 = 51\) 個

モデルのオプション設定

options were - softmax modelling decay=0.01 の行は、モデルの挙動を決定する設定を確認するものです。

softmax modelling: 引数 softmax = TRUE が適用されていることを意味します。出力層の値をそのまま使うのではなく、ソフトマックス関数を通して「確率（総和が1になる値）」に変換しています。この設定により、モデルの出力は「クラス1である確率、クラス2である確率…」として解釈可能となり、多クラス分類問題に適した形式となります。
decay=0.01: 引数 decay = 0.01 が適用されていることを示します。これは正則化項であり、重みの値が不必要に大きくなることを防いでいます。この設定が存在することで、学習データのみに過剰適合（オーバーフィッティング）することなく、滑らかな分類境界が得られています。

結果の可視化

# 描画領域の分割 (1行2列)
par(mfrow = c(1, 2))

# --- プロット1: 回帰結果 ---
plot(
  x_reg, y_noise,
  main = "ニューラルネットワークによる\n非線形回帰",
  xlab = "入力変数 X",
  ylab = "目的変数 Y",
  pch = 16,
  col = rgb(0, 0, 0, 0.3), # 半透明の黒
  cex = 1.2
)
# 真の関数（点線）
lines(x_reg, y_true, col = "blue", lwd = 2, lty = 2)
# nnetによる予測（赤線）
lines(x_reg, pred_reg, col = "red", lwd = 3)
legend(
  "topright",
  legend = c("観測データ", "真の関数 (sin)", "nnet予測値"),
  col = c("black", "blue", "red"),
  pch = c(16, NA, NA),
  lty = c(NA, 2, 1),
  lwd = c(NA, 2, 3),
  bty = "n"
)

# --- プロット2: 分類結果 ---
# 背景に分類境界を描画
# クラスごとに色を割り当て (1:中心, 2:中間, 3:外側)
image(
  grid_seq, grid_seq,
  matrix(pred_grid_class, nrow = 100, ncol = 100),
  col = c("#FFCCCC", "#CCFFCC", "#CCCCFF"), # 淡い赤、緑、青
  main = "ニューラルネットワークによる\n多クラス分類",
  xlab = "特徴量 1",
  ylab = "特徴量 2"
)

# 学習データをプロット
# 元のクラス名に合わせて色を指定
point_cols <- c("red", "green", "blue")
points(
  df_cls$x1, df_cls$x2,
  pch = 21,
  bg = point_cols[as.numeric(df_cls$class)],
  col = "white",
  cex = 1.0
)
legend(
  "topright",
  legend = levels(df_cls$class),
  pt.bg = point_cols,
  pch = 21,
  col = "white",
  title = "正解クラス",
  bg = "white"
)

左図：ニューラルネットワークによる非線形回帰

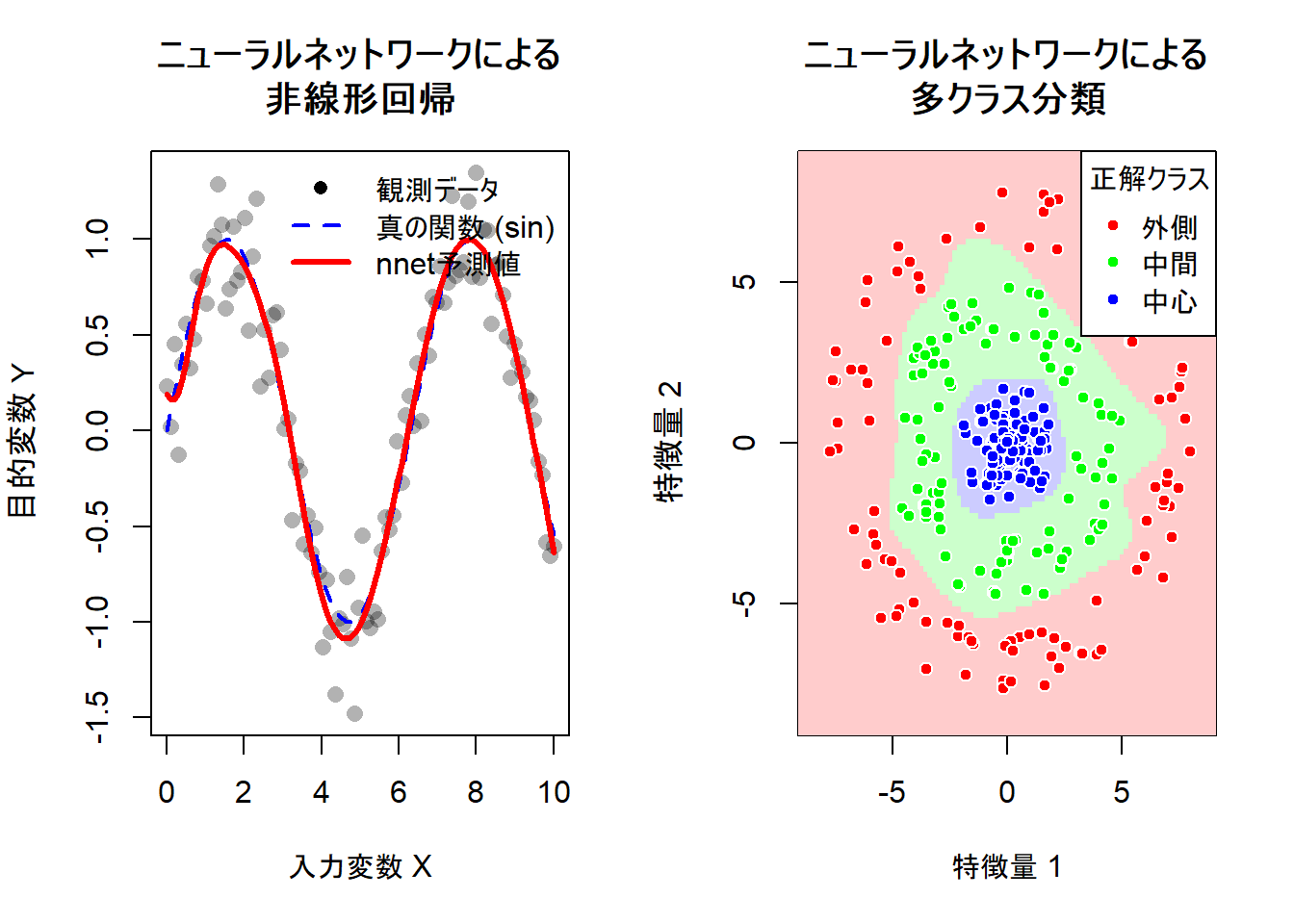
Figure 1 の左図は、ノイズを含んだ正弦波データに対して、linout = TRUE を設定したニューラルネットワークがどのように適合（フィッティング）したかを示しています。

灰色の点は観測データであり、正弦波（青い破線）にランダムなノイズが加わっています。ニューラルネットワークの予測線である赤い実線に注目すると、個々の点のランダムな上下動（ノイズ）に過剰に反応することなく、データの背後にある「真の構造（青い破線）」をほぼトレースしていることがわかります。
単回帰分析のような直線モデルでは、このような波打つ曲線を捉えることは不可能です。隠れ層に10個のニューロン（size = 10）を用意したことで、モデルは十分な「曲がる」自由度を獲得し、山や谷の形状を再現しています。
Y軸の値を見ると、-1.0から1.0の範囲を超えてデータが分布しています。linout = TRUE と設定したことで、出力層が値を制限することなく、そのままの実数値を予測できていることが確認できます。

右図：ニューラルネットワークによる多クラス分類

Figure 1 の右図は、同心円状に分布する3つのクラス（中心、中間、外側）を、softmax = TRUE を設定したニューラルネットワークがどのように分離したかを示しています。

データ点（赤・緑・青の丸）は同心円状に並んでおり、これらを一本の直線で分けることは不可能です。しかし、背景色の塗り分け（決定境界）を見ると、モデルは中心部を青、その周囲を緑、最外周を赤というように、「ドーナツ状」の領域を作り出しています。これは、隠れ層が入力空間を歪め、非線形な境界線を引く能力を持っていることを示唆しています。
緑と赤の境界付近を見ると、境界線は個々のデータ点を無理やり避けるようにギザギザしているのではなく、ある程度滑らかな曲線を描いています。これは decay（重み減衰）パラメータが働き、過学習（オーバーフィッティング）を抑制していることを示唆しています。未知のデータが境界付近に来ても、妥当な予測ができる状態です。
背景色は、その地点における予測確率が最も高いクラスを表しています。境界付近で色が切り替わる様子は、確率の逆転が起きている場所（決定境界）を視覚的に捉えたものです。

以上です。