Rの関数から rmultireg {bayesm} を確認します。
関数 rmultireg とは
関数 rmultireg は、多変量線形回帰モデル(Multivariate Linear Regression Model) において、自然共役事前分布(Natural Conjugate Prior)を用いた場合の事後分布から、パラメータの無作為抽出を行う関数です。
単変量の回帰分析を複数の目的変数(従属変数)に拡張したモデルであり、以下の構造を持ちます。
\[ Y = XB + U \] ここで、
- \(Y\):
- \(n \times m\) の目的変数行列(\(n\) は観測数、\(m\) は目的変数の数)
- \(X\):
- \(n \times k\) の説明変数行列(\(k\) は説明変数の数)
- \(B\):
- \(k \times m\) の回帰係数行列
- \(U\):
- \(n \times m\) の誤差項行列。各行は \(N(0, \Sigma)\) に従うと仮定されます。
- \(\Sigma\):
- 誤差分散共分散行列
関数 rmultireg の引数
library(bayesm)
args(rmultireg)function (Y, X, Bbar, A, nu, V)
NULL-
Y(\(n \times m\) matrix):- 目的変数(従属変数)のデータ行列です。
- \(n\) は観測数(サンプルサイズ)、\(m\) は目的変数の数です。単変量回帰ではなく多変量回帰であるため、複数の目的変数を同時に扱います。
-
X(\(n \times k\) matrix):- 説明変数(独立変数)のデータ行列です。
- \(k\) は説明変数の数です。切片項を含める場合、最初の列はすべて1のベクトルとします。
-
Bbar(\(k \times m\) matrix):- 回帰係数行列 \(B\) の事前平均(Prior Mean)です。
- 事前知識として想定する係数の値を設定します。情報がない場合(無情報事前分布に近い形にしたい場合)は、すべて0の行列を指定することが可能です。
-
A(\(k \times k\) matrix):- 回帰係数 \(B\) に対する事前精度の行列(Prior Precision Matrix)です。
- 分散ではなく「精度(分散の逆数)」である点に注意が必要です。対角成分の値を小さく設定すると(例: 0.01)、分散は大きくなり、事前情報の影響を弱くした「拡散した事前分布」を表現できます。逆に値を大きくすると、事前平均
Bbarへの確信度が強いことを意味します。
-
nu(integer / scalar):- 共分散行列 \(\Sigma\) の事前分布(逆ウィシャート分布)における自由度パラメータ(d.f. parameter)です。
-
V(\(m \times m\) matrix):- 共分散行列 \(\Sigma\) の事前分布(逆ウィシャート分布)における尺度行列(Scale Matrix / Location Parameter)です。
- 事前に想定される誤差の分散共分散構造を指定します。
シミュレーション用サンプルデータの作成とコード
それでは、rmultireg の動作を確認するために、サンプルデータを作成し、事後分布からのサンプリングを行います。
ここでは、真のパラメータ(係数 \(B\) と分散共分散行列 \(\Sigma\))をあらかじめ定義し、それに基づいてデータを生成します。
その後、rmultireg を繰り返し呼び出すことで事後分布を形成し、その平均値が真のパラメータを適切に復元できるかを確認します。
サンプルデータの作成
# ライブラリの読み込み
library(bayesm)
library(MASS) # 多変量正規分布の乱数生成に使用
# 乱数シードの設定
seed <- 20251209
set.seed(seed)
# データの次元設定
n_obs <- 500 # 観測数 (n)
n_vars <- 3 # 説明変数の数 (k, 切片含む)
n_resp <- 2 # 目的変数の数 (m)
# 説明変数行列 X の生成 (n x k)
# 第1列は切片項として1、残りは標準正規分布から生成
X <- cbind(1, matrix(rnorm(n_obs * (n_vars - 1)), nrow = n_obs))
colnames(X) <- c("切片", "変数1", "変数2")
# 真の回帰係数行列 B_true (k x m)
# これが推定のターゲットとなる真の値です
B_true <- matrix(c(
2.0, 0.5, # 切片: Y1は2.0, Y2は0.5
1.5, -1.0, # 変数1: Y1に正の影響, Y2に負の影響
-0.8, 0.8 # 変数2: Y1に負の影響, Y2に正の影響
), nrow = n_vars, byrow = TRUE)
colnames(B_true) <- c("Y1", "Y2")
rownames(B_true) <- c("切片", "変数1", "変数2")
# 真の誤差分散共分散行列 Sigma_true (m x m)
# Y1とY2の間には相関があると仮定します
Sigma_true <- matrix(c(
1.0, 0.5,
0.5, 1.0
), nrow = n_resp)
# 誤差項 U の生成
U <- mvrnorm(n = n_obs, mu = rep(0, n_resp), Sigma = Sigma_true)
# 目的変数行列 Y の生成 (モデル: Y = XB + U)
Y <- X %*% B_true + U
colnames(Y) <- c("Y1", "Y2")
cat("--- 真のパラメータ B ---\n")
print(B_true)
cat("\n--- 真のパラメータ Sigma ---\n")
print(Sigma_true)
cat("\n")--- 真のパラメータ B ---
Y1 Y2
切片 2.0 0.5
変数1 1.5 -1.0
変数2 -0.8 0.8
--- 真のパラメータ Sigma ---
[,1] [,2]
[1,] 1.0 0.5
[2,] 0.5 1.0\(\beta\) の真の値として、Y1 に対しては (2.0, 1.5, -0.8)、Y2 に対しては (0.5, -1.0, 0.8) を設定しました。また、誤差項には \(\Sigma_{true}\) に基づく相関を持たせています。
rmultireg を用いた推定の準備
# 事前分布のハイパーパラメータ設定
# ここでは比較的「情報の少ない」事前分布を設定します
# Bの事前平均 Bbar (0で設定)
Bbar <- matrix(0, nrow = n_vars, ncol = n_resp)
# Bの事前精度行列 A (小さな値 = 大きな分散 = 弱い事前情報)
A <- 0.01 * diag(n_vars)
# Sigmaの事前分布の自由度 nu (最小限の値)
nu <- n_resp + 3
# Sigmaの事前尺度行列 V (事前情報を弱めるため、単位行列を使用)
V <- nu * diag(n_resp)シミュレーションの実行
# rmultireg は1回の呼び出しで事後分布から1つのサンプルを返します。
# 事後分布全体を把握するため、繰り返し呼び出して多数のサンプルを蓄積します。
R_draws <- 10000 # シミュレーション回数
B_samples <- array(0, dim = c(n_vars, n_resp, R_draws))
Sigma_samples <- array(0, dim = c(n_resp, n_resp, R_draws))
for (r in 1:R_draws) {
# rmultireg の実行
out <- rmultireg(Y, X, Bbar, A, nu, V)
# 結果の格納
B_samples[, , r] <- out$B
Sigma_samples[, , r] <- out$Sigma
}関数 rmultireg は「自然共役事前分布」を利用しているため、MCMCのような連鎖的な依存関係はありません。
それゆえ、単純な for ループで繰り返し rmultireg を呼び出すことは、解析的な事後分布から直接独立サンプリング(Monte Carlo simulation)を行っていることと同義です。
結果の確認
# 事後平均の計算
B_posterior_mean <- apply(B_samples, c(1, 2), mean)
Sigma_posterior_mean <- apply(Sigma_samples, c(1, 2), mean)
colnames(B_posterior_mean) <- colnames(Y)
rownames(B_posterior_mean) <- colnames(X)
cat("--- 推定された B の事後平均 ---\n")
print(round(B_posterior_mean, 4))
cat("\n--- 推定された Sigma の事後平均 ---\n")
print(round(Sigma_posterior_mean, 4))--- 推定された B の事後平均 ---
Y1 Y2
切片 2.0270 0.4851
変数1 1.4868 -1.0665
変数2 -0.8786 0.8059
--- 推定された Sigma の事後平均 ---
[,1] [,2]
[1,] 0.9179 0.4591
[2,] 0.4591 0.9936回帰係数行列 \(B\) の推定結果について
- 切片(Intercept):
- 真の値は \(Y1\) に対して 2.0、\(Y2\) に対して 0.5 です。推定値はそれぞれ 2.0270、0.4851 となっており、中心傾向を捉えています。
- 変数1(Variable 1):
- 真の値は \(Y1\) に対して 1.5、\(Y2\) に対して -1.0 です。推定値は 1.4868、-1.0665 であり、符号を含めて影響の大きさが適切に推定されています。
- 変数2(Variable 2):
- 真の値は \(Y1\) に対して -0.8、\(Y2\) に対して 0.8 です。推定値は -0.8786、0.8059 であり、変数2も、符号を含めて影響の大きさが適切に推定されています。
誤差分散共分散行列 \(\Sigma\) の推定結果について
- 分散(対角成分):
- 真の値は両変数ともに 1.0 です。推定値は \(Y1\) の分散が 0.9179、\(Y2\) の分散が 0.9936 となり、真の分散に近い値が算出されています。
- 共分散(非対角成分):
- 真の値は 0.5 です。推定値は 0.4591 となっており、2つの目的変数 \(Y1\) と \(Y2\) の間に存在する正の相関関係をモデルが検知しています。
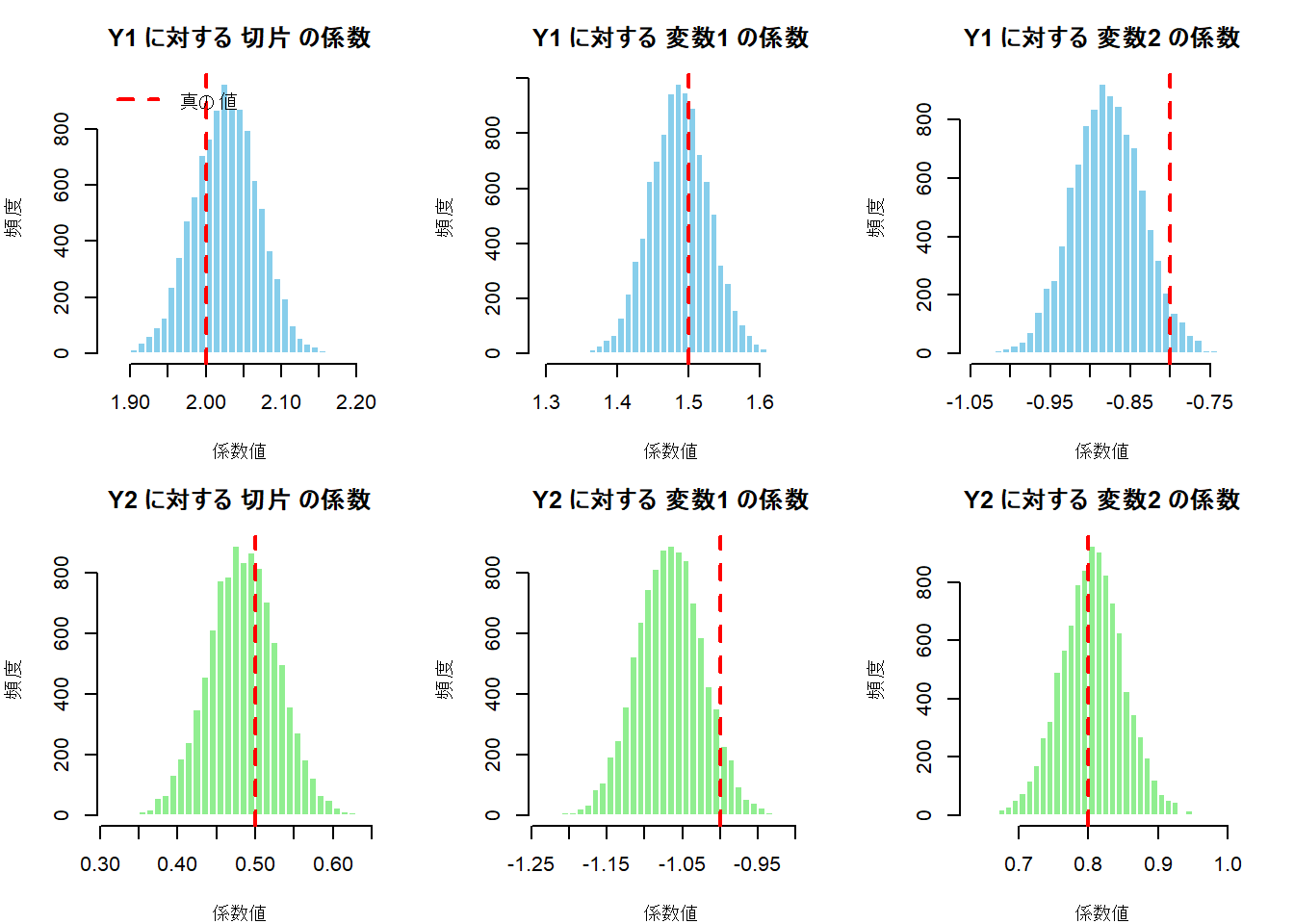
事後分布の可視化
# プロット領域の設定: 2行3列
# 1行目: Y1 に対する各変数の係数
# 2行目: Y2 に対する各変数の係数
par(mfrow = c(2, 3), mar = c(4, 4, 3, 2))
# 変数名と目的変数名の定義
var_labels <- c("切片", "変数1", "変数2")
resp_labels <- c("Y1", "Y2")
plot_colors <- c("skyblue", "lightgreen") # Y1用とY2用の色
# ループによる描画
for (j in 1:2) { # j=1 は Y1, j=2 は Y2
for (i in 1:3) { # i=1:切片, i=2:変数1, i=3:変数2
# ヒストグラムの描画
hist(B_samples[i, j, ],
breaks = 40,
col = plot_colors[j],
border = "white",
main = paste(resp_labels[j], "に対する", var_labels[i], "の係数"),
xlab = "係数値",
ylab = "頻度"
)
# 真の値を赤線で描画
abline(v = B_true[i, j], col = "red", lwd = 2, lty = 2)
# 凡例の追加
if (i == 1 && j == 1) {
legend("topleft", legend = "真の値", col = "red", lty = 2, lwd = 2, bty = "n", cex = 1.1)
}
}
}95%信用区間の算出
# 変数名と目的変数名の取得
var_names <- rownames(B_posterior_mean)
resp_names <- colnames(B_posterior_mean)
# 各目的変数ごとにループして結果を表示
for (j in 1:length(resp_names)) {
cat(paste0("=== 目的変数 ", resp_names[j], " に対する回帰係数の要約 ===\n"))
# 結果を格納するための行列を作成
# 列構成: 事後平均, 下側2.5%, 上側97.5%
summary_table <- matrix(NA, nrow = length(var_names), ncol = 3)
rownames(summary_table) <- var_names
colnames(summary_table) <- c("事後平均", "下側2.5%", "上側97.5%")
# 各説明変数について計算
for (i in 1:length(var_names)) {
# 該当するパラメータの全サンプルを抽出
draws <- B_samples[i, j, ]
# 平均と分位点の計算
post_mean <- mean(draws)
ci <- quantile(draws, probs = c(0.025, 0.975))
# 行列に格納
summary_table[i, 1] <- post_mean
summary_table[i, 2] <- ci[1]
summary_table[i, 3] <- ci[2]
}
# 結果の出力
print(round(summary_table, 4))
cat("\n")
}
# 真の値の再確認(比較用)
cat("=== 参考: 真のパラメータ値 (B_true) ===\n")
print(B_true)=== 目的変数 Y1 に対する回帰係数の要約 ===
事後平均 下側2.5% 上側97.5%
切片 2.0270 1.9426 2.1090
変数1 1.4868 1.4069 1.5693
変数2 -0.8786 -0.9634 -0.7905
=== 目的変数 Y2 に対する回帰係数の要約 ===
事後平均 下側2.5% 上側97.5%
切片 0.4851 0.3971 0.5727
変数1 -1.0665 -1.1520 -0.9810
変数2 0.8059 0.7158 0.8956
=== 参考: 真のパラメータ値 (B_true) ===
Y1 Y2
切片 2.0 0.5
変数1 1.5 -1.0
変数2 -0.8 0.86つの真のパラメータ値は、いずれも95%信用区間内に収まっていることを確認できます。
以上です。