Rの関数:difference_in_means {estimatr}

# パッケージの読み込み
library(ggplot2)
library(dplyr)

# 乱数シードの固定
seed <- 20251212
set.seed(seed)

# 設定: 教育プログラムの実験
# 地域（ブロック）: 都市部 (Urban) と 地方部 (Rural)
# クラスター: 学校のクラス単位でプログラムを導入するか決定
# 個人: 生徒

# パラメータ設定
n_blocks <- 2 # 都市部、地方部
n_clusters_per_block <- 20 # 各地域に20クラスずつ
n_students_per_cluster <- 15 # 1クラス15人
Total_N <- n_blocks * n_clusters_per_block * n_students_per_cluster

# データの骨組み作成
data_sim <- data.frame(
  block_id = rep(c("都市部", "地方部"), each = n_clusters_per_block * n_students_per_cluster),
  cluster_id = rep(1:(n_blocks * n_clusters_per_block), each = n_students_per_cluster)
)

# 処置の割り当て
cluster_treatment <- data_sim %>%
  group_by(block_id, cluster_id) %>%
  summarise(temp = 1, .groups = "drop") %>%
  group_by(block_id) %>%
  mutate(treatment = sample(rep(c(0, 1), length.out = n()))) %>%
  ungroup() %>%
  select(cluster_id, treatment)

# データを結合
data_sim <- left_join(data_sim, cluster_treatment, by = "cluster_id")

# 変数の生成
base_score_block <- ifelse(data_sim$block_id == "都市部", 60, 50)
cluster_noise_vals <- rnorm(n_blocks * n_clusters_per_block, mean = 0, sd = 5)
data_sim$cluster_noise <- cluster_noise_vals[data_sim$cluster_id]
individual_noise <- rnorm(Total_N, mean = 0, sd = 8)
true_effect <- 5

data_sim$score <- base_score_block +
  (true_effect * data_sim$treatment) +
  data_sim$cluster_noise +
  individual_noise

data_sim$treatment_label <- ifelse(data_sim$treatment == 1, "実施あり", "実施なし")

cat("--- データの一部を確認 ---\n")
print(str(data_sim))

cat("\n--- データ概要 ---\n")
cat(sprintf("総観測数: %d 人\n", nrow(data_sim)))
cat(sprintf("ブロック数: %d (都市部, 地方部)\n", length(unique(data_sim$block_id))))
cat(sprintf("クラスター数: %d (クラス単位)\n", length(unique(data_sim$cluster_id))))
cat(sprintf("真の処置効果: %+.1f 点", true_effect))

# データの可視化
p1 <- ggplot(data_sim, aes(x = treatment_label, y = score, fill = treatment_label)) +
  geom_boxplot(alpha = 0.6) +
  facet_wrap(~block_id) +
  labs(
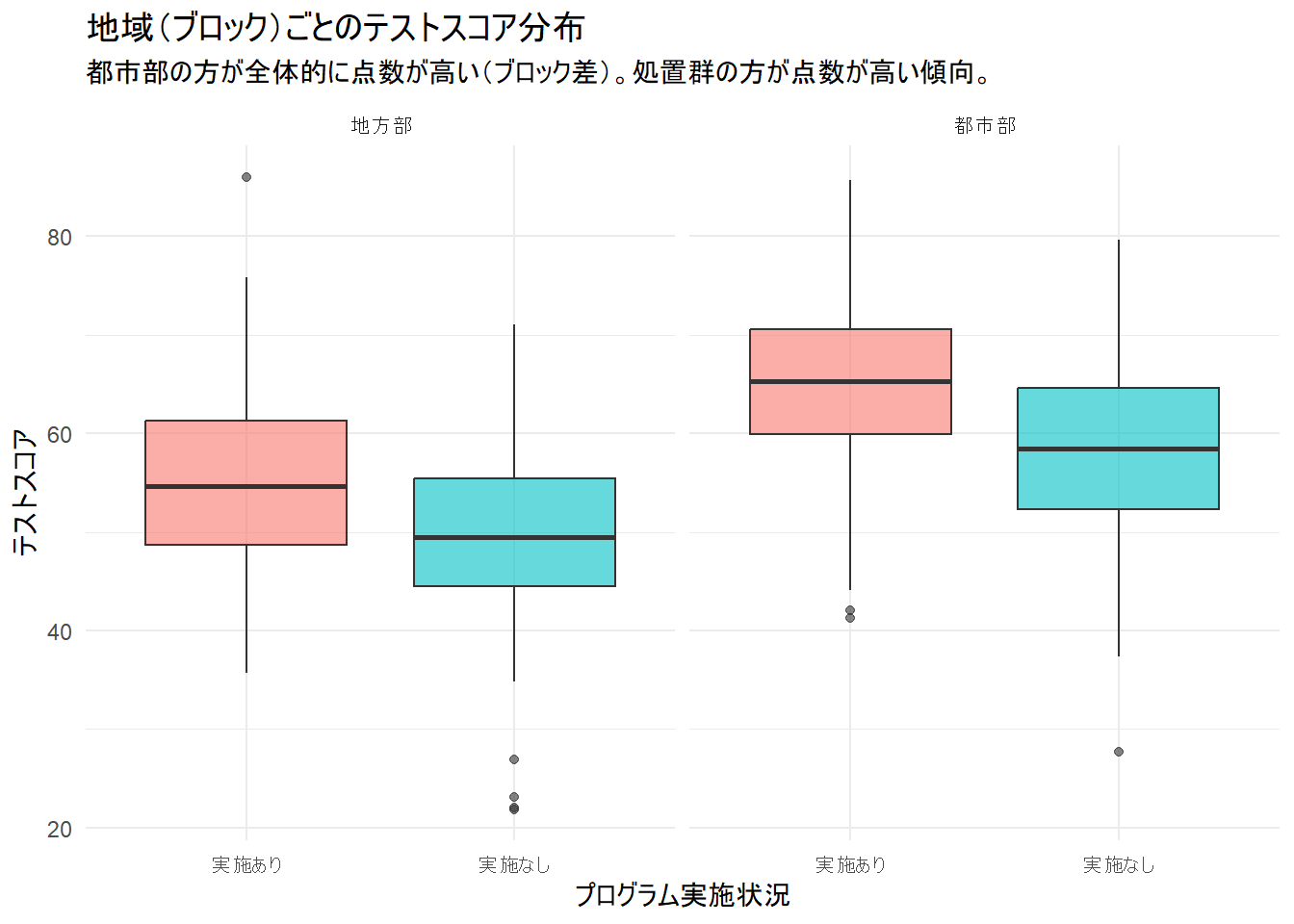
    title = "地域（ブロック）ごとのテストスコア分布",
    subtitle = "都市部の方が全体的に点数が高い（ブロック差）。処置群の方が点数が高い傾向。",
    x = "プログラム実施状況",
    y = "テストスコア"
  ) +
  theme_minimal() +
  theme(legend.position = "none")

print(p1)