Rの関数から horvitz_thompson {estimatr} を確認します。
本ポストはこちらの続きです。

関数 horvitz_thompson とは
horvitz_thompson は、Horvitz-Thompson 推定量(IPW: Inverse Probability Weighting、逆確率重み付け推定量)を用いて、平均処置効果(ATE)を推定するための関数です。
この手法の特徴は、各観測データが「サンプルに含まれる確率(処置割り当て確率)」の逆数を重みとして使用する点にあります。
例えば、ある個体が処置群に割り当てられる確率が低い(例: 20%)にもかかわらず、実際に処置を受けたとします。
この場合、その個体は「希少な存在」であるため、分析において 5倍(1/0.2)の重みを与えて評価します。
単純なランダム化実験(全員が50%の確率で割り付けられる等)では、通常の平均の差と結果は一致しますが、Horvitz-Thompson 推定量 は、割り付け確率が個体やグループによって異なる複雑な実験デザインにおいて、バイアスを取り除いた推定を行うための手法になります。
関数 horvitz_thompson の引数
library(estimatr)
args(horvitz_thompson)function (formula, data, blocks, clusters, simple = NULL, condition_prs,
condition_pr_mat = NULL, ra_declaration = NULL, subset, condition1 = NULL,
condition2 = NULL, se_type = c("youngs", "constant", "none"),
ci = TRUE, alpha = 0.05, return_condition_pr_mat = FALSE)
NULL-
formula- 解析モデルを指定する式です。形式は
outcome ~ treatment(被説明変数 ~ 処置変数)となります。 - 右辺には処置変数を1つだけ指定します。
- 解析モデルを指定する式です。形式は
-
data- 解析対象のデータフレームです。
-
condition_prs- 各個体が、実際に割り当てられた「処置群(condition2)」に割り付けられる確率(Propensity Score)を指定するベクトルです。
- Horvitz-Thompson 推定量の計算における最も重要な情報です。この確率の逆数が重みとして利用されます。指定しない場合、ブロックやクラスターの情報から推定しようと試みられますが、複雑なデザインの場合は明示的な指定が推奨されます。
-
blocks- ブロック(層化)変数を指定します。
- デザインがブロック化されている場合、ブロックごとの確率行列を生成するために使用されます。
-
clusters- クラスター変数を指定します。
- デザインがクラスター化されている場合、クラスター単位での同時生起確率を考慮するために使用されます。
-
simple- 単純無作為割り付け(Simple Random Assignment: コイントスのように独立)を仮定するかどうかの論理値です。
- デフォルト:
NULL(状況により自動判定)。TRUEの場合はベルヌーイ試行を仮定し、FALSEの場合は完全無作為割り付け(固定数割り付け)を仮定します。
-
se_type- 分散(標準誤差)の推定方法を指定します。
-
"youngs"(デフォルト、保守的な分散推定量)、"constant"(定数処置効果モデルを仮定)、"none"(なし)。
-
condition1,condition2- 比較対象となる2つの群を指定します。通常、
condition1が対照群(Control)、condition2が処置群(Treatment)となります。
- 比較対象となる2つの群を指定します。通常、
-
ra_declaration-
randomizrパッケージで作成された割り付け宣言オブジェクトを指定します。これを渡すと、確率やデザイン情報を自動的に読み取ります。
-
-
ci,alpha- 信頼区間の計算有無(
TRUE/FALSE)と有意水準(デフォルト0.05)です。
- 信頼区間の計算有無(
シミュレーションコード
以下に、horvitz_thompson の挙動を確認するためのシミュレーションコードを示します。
シナリオ: 顧客ロイヤリティに応じたクーポン配布実験
あるECサイトがクーポン配布の効果を測定しようとしています。しかし、全員にランダムに配るのではなく、戦略的に以下のルールで配布しました。
- 優良顧客(Loyal):
- クーポンへの反応が良いと期待されるため、80%の高確率でクーポンを配布。
- 一般顧客(Normal):
- 予算削減のため、20%の低確率でクーポンを配布。
問題点:
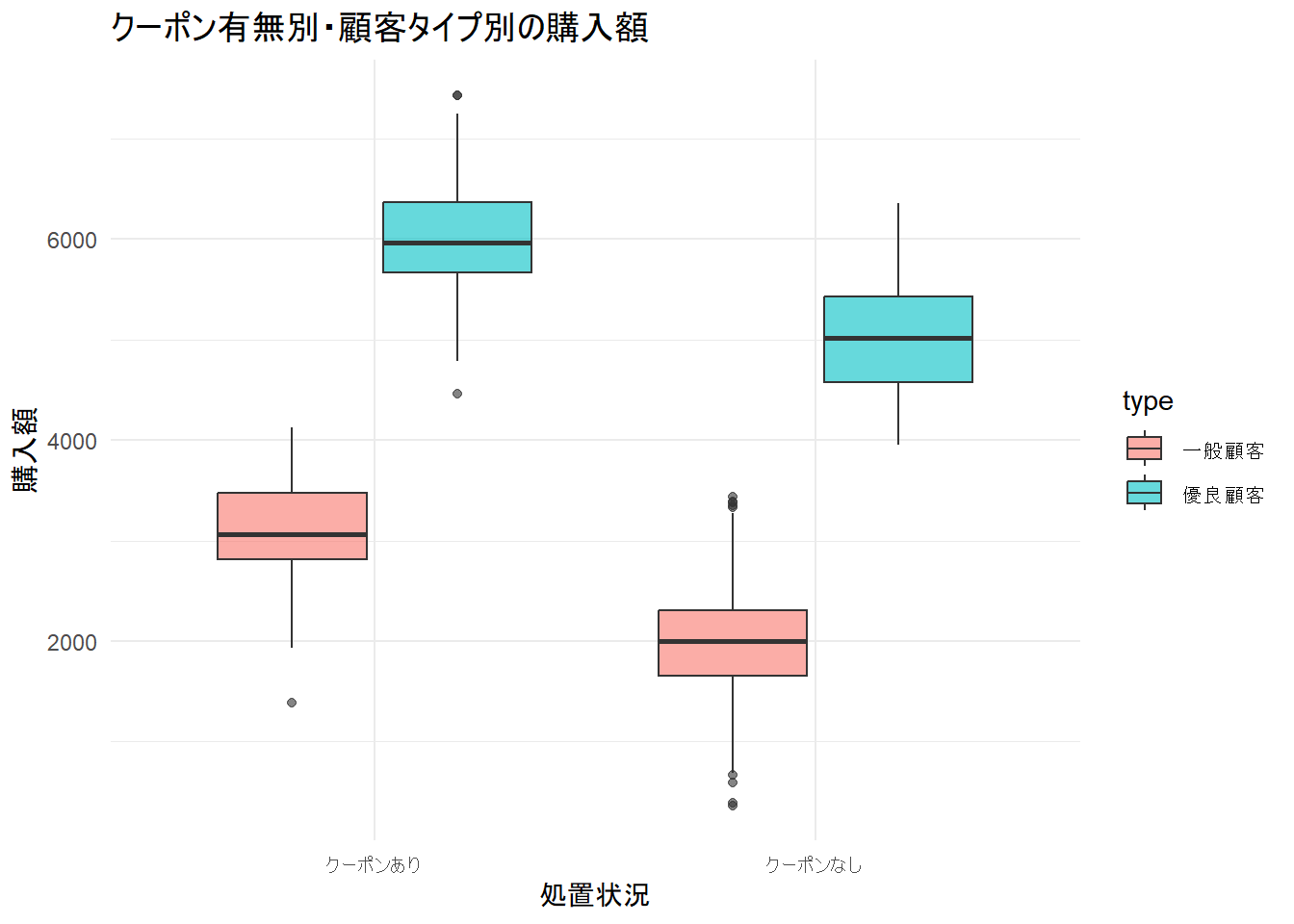
優良顧客はクーポンがなくても購入額が高い傾向にあります。
単純に「クーポンあり vs なし」で比較すると、クーポンあり群には「元々たくさん買う優良顧客」が大量に含まれることになります。
結果として、クーポンの効果が過大評価(セレクションバイアス)されてしまいます。
horvitz_thompson を用いて、割り付け確率の違い(80%と20%)を補正し、真の効果を推定できるか検証します。
なお、有意水準は5%とします。
シミュレーションデータの生成
# パッケージの読み込み
library(ggplot2)
library(dplyr)
# 乱数シードの固定
seed <- 20251214
set.seed(seed)
# サンプルサイズ
N <- 1000
# 顧客データの生成
# 顧客タイプ: 30%が優良顧客、70%が一般顧客
type_preferred <- 0.3
type_general <- 0.7
df_sim <- data.frame(
id = 1:N,
type = sample(c("優良顧客", "一般顧客"), N, replace = TRUE, prob = c(type_preferred, type_general))
)
# 割り付け確率の設定
# 優良顧客は 80% の確率でクーポン配布 (Z=1)
# 一般顧客は 20% の確率でクーポン配布 (Z=1)
coupon_preferred <- 0.8
coupon_general <- 0.2
df_sim$prob_assign <- ifelse(df_sim$type == "優良顧客", coupon_preferred, coupon_general)
# 処置(クーポン配布)の実行
df_sim$treatment <- rbinom(N, size = 1, prob = df_sim$prob_assign)
# 潜在的な購入額(Potential Outcomes)の生成
# ベースライン購入額: 優良顧客は平均5000円、一般顧客は平均2000円
baseline_preferred <- 5000
baseline_general <- 2000
base_amount <- ifelse(df_sim$type == "優良顧客", baseline_preferred, baseline_general) + rnorm(N, 0, 500)
# 真の処置効果(クーポンの効果): 一律 +1000円 とする
true_effect <- 1000
# 観測される購入額 Y
# 処置群 (Z=1) なら +1000円 される
df_sim$outcome <- base_amount + (true_effect * df_sim$treatment)
# 処置変数のラベル化
df_sim$treatment_label <- ifelse(df_sim$treatment == 1, "クーポンあり", "クーポンなし")
cat("--- データ概要 ---\n")
cat(sprintf("総観測数: %d 人\n", N))
cat(sprintf("割り付け確率: 優良顧客 = %d%%, 一般顧客 = %d%% \n", coupon_preferred * 100, coupon_general * 100))
cat(sprintf("ベースライン購入額: 優良顧客 = %d円, 一般顧客 = %d円\n", baseline_preferred, baseline_general))
cat(sprintf("真のクーポン効果: +%d 円\n\n", true_effect))--- データ概要 ---
総観測数: 1000 人
割り付け確率: 優良顧客 = 80%, 一般顧客 = 20%
ベースライン購入額: 優良顧客 = 5000円, 一般顧客 = 2000円
真のクーポン効果: +1000 円分析1: 単純な平均の差(Naive Difference)
# 確率の違いを無視して差を計算
naive_model <- lm(outcome ~ treatment, data = df_sim)
naive_est <- coef(naive_model)["treatment"]
print(summary(naive_model))
cat("------------------------------------------------------------\n")
cat(sprintf("単純比較による推定効果: %.1f 円\n", naive_est))
Call:
lm(formula = outcome ~ treatment, data = df_sim)
Residuals:
Min 1Q Median 3Q Max
-3595.3 -671.0 -90.8 711.5 4105.4
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2256.12 48.27 46.74 <2e-16 ***
treatment 2723.82 78.73 34.60 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1206 on 998 degrees of freedom
Multiple R-squared: 0.5453, Adjusted R-squared: 0.5449
F-statistic: 1197 on 1 and 998 DF, p-value: < 2.2e-16
------------------------------------------------------------
単純比較による推定効果: 2723.8 円分析2: Horvitz-Thompson 推定量(estimatr)
# 割り付け確率 (condition_prs) を明示して補正を行う
ht_model <- horvitz_thompson(
formula = outcome ~ treatment,
data = df_sim,
condition_prs = prob_assign, # 各個体の割り付け確率を指定
se_type = "youngs"
)
# 結果の表示
print(ht_model)
cat("------------------------------------------------------------\n")
# 結果の抽出
ht_est <- ht_model$coefficients
ht_se <- ht_model$std.error
ht_ci_low <- ht_model$conf.low
ht_ci_high <- ht_model$conf.high
cat(sprintf("Horvitz-Thompson 推定値: %.1f 円\n", ht_est))
cat(sprintf("標準誤差: %.1f\n", ht_se))
cat(sprintf("95%%信頼区間: [%.1f, %.1f]\n", ht_ci_low, ht_ci_high)) Estimate Std. Error t value Pr(>|t|) CI Lower CI Upper DF
treatment 1090.86 293.1832 3.720746 0.0001986352 516.2317 1665.489 NA
------------------------------------------------------------
Horvitz-Thompson 推定値: 1090.9 円
標準誤差: 293.2
95%信頼区間: [516.2, 1665.5]分析結果の確認
単純比較の過大評価
まず、通常の線形回帰(lm)の結果を確認します。
- 推定値: 2723.8 円
- 真の効果: 1000 円
- 誤差: 約 +1724 円 の過大評価
p-value: < 2e-16と設定した有意水準を下回っていますが、クーポンを受け取ったグループ(処置群)の大半が、元々お金を使ってくれる「優良顧客(割り付け確率80%)」で占められており、この +2724円 という数字は、純粋なクーポンの効果(1000円)に、「優良顧客と一般顧客の元々の購入額の差(約3000円分の一部)」が混ざり込んでしまった結果です。
Horvitz-Thompson 推定
次に、horvitz_thompson の結果を確認します。
- 推定値: 1090.9 円
- 真の効果: 1000 円
- 誤差: +90 円 程度
推定値が補正され、真の効果である1000円に近い値となりました。95%信頼区間 [516.2, 1665.5] も、真の値を含んでいます。
これは、関数内部で以下の「重み付け」が行われた結果です。
- 処置を受けた一般顧客:
- 5倍(1/0.2)の重みを与えて重視します。
- 処置を受けた優良顧客:
- 1.25倍(1/0.8)の重みに抑えます。
この重み付けにより、優良顧客ばかりで膨れ上がっていた処置群の偏りが解消され、公平な比較が可能になりました。
標準誤差の拡大
標準誤差(Std. Error)を比較すると、以下のようになっています。
- 単純比較: 78.73
- Horvitz-Thompson: 293.2
Horvitz-Thompson の方が標準誤差が大きくなっています。
これは、重み付け(特に大きな重みを持つデータの存在)によって推定の分散が大きくなった結果であり、単純比較の「78.73」という、Horvitz-Thompsonより小さな誤差は、「データが偏っていることを無視した上での、見せかけの精度の高さ」に過ぎません。
以上です。