Rの関数から MCMCglmm {MCMCglmm} を確認します。
関数 MCMCglmm とは
パッケージ MCMCglmm は、マルコフ連鎖モンテカルロ法(MCMC)を用いて一般化線形混合モデル(GLMM)を適合させるための関数です。
ベイズ推定の枠組みを採用しており、正規分布だけでなく、ポアソン分布、二項分布、多項分布、順序ロジスティック回帰など、多様な確率分布(ファミリー)に対応しています。
また、複雑な分散共分散構造を扱える点が特徴の一つです。
関数 MCMCglmm の引数
MCMCglmm 関数は、固定効果、変量効果、および残差構造を指定し、指定された事前分布とMCMCの設定に基づいて事後分布をサンプリングします。
library(MCMCglmm)
args(MCMCglmm)function (fixed, random = NULL, rcov = ~units, family = "gaussian",
mev = NULL, data, start = NULL, prior = NULL, tune = NULL,
pedigree = NULL, nodes = "ALL", scale = TRUE, nitt = 13000,
thin = 10, burnin = 3000, pr = FALSE, pl = FALSE, verbose = TRUE,
DIC = TRUE, singular.ok = FALSE, saveX = TRUE, saveZ = TRUE,
saveXL = TRUE, slice = FALSE, ginverse = NULL, trunc = FALSE,
theta_scale = NULL, saveWS = TRUE)
NULLモデル指定引数
-
fixed:- (必須) 固定効果を指定するモデル式(formula)です。例:
y ~ x1 + x2。左辺に応答変数を、右辺に説明変数を記述します。
- (必須) 固定効果を指定するモデル式(formula)です。例:
-
random:- 変量効果を指定するモデル式です。例:
~ id + region。デフォルトはNULLですが、混合モデルを構築する際はここにグループ化変数を指定します。idh(),us()などを用いて分散共分散構造を指定可能です。
- 変量効果を指定するモデル式です。例:
-
rcov:- 残差の分散共分散構造を指定するモデル式です。デフォルトは
~ unitsであり、これは各データ点に対して独立した誤差項(等分散)を仮定することを意味します。多変量モデルでは~ us(trait):unitsのように指定し、形質間の相関を考慮します。
- 残差の分散共分散構造を指定するモデル式です。デフォルトは
-
family:- 応答変数の確率分布を指定します。デフォルトは
"gaussian"(正規分布)です。"poisson","categorical"(多項/二項),"ordinal"(順序),"zipoisson"(ゼロ過剰ポアソン) など多数の分布に対応しています。
- 応答変数の確率分布を指定します。デフォルトは
-
data:- (必須) モデル式に含まれる変数を含むデータフレームです。
-
prior:- 固定効果(
B)、変量効果(G)、残差(R)に対する事前分布を指定するリストです。指定しない場合はデフォルトの事前分布が使用されます。
- 固定効果(
MCMC制御引数
-
nitt:- MCMCの総反復回数(イテレーション数)です。デフォルトは 13,000 です。
-
thin:- サンプリングの間引き間隔(間引き数)です。自己相関を減らすために使用されます。デフォルトは 10 です。
-
burnin:- バーンイン期間(初期の捨てられるサンプル数)です。定常分布に収束する前の系列を除外します。デフォルトは 3,000 です。
-
start:- MCMCの初期値を指定するリストです。
G(変量効果の分散)、R(残差分散)などの初期値を設定できます。指定がない場合は自動的に生成されます。
- MCMCの初期値を指定するリストです。
-
tune:- メトロポリス・ヘイスティングス法の提案分布の分散などを調整するためのリストです。特定の分布(順序データなど)で潜在変数を更新する際に必要となります。
特殊なモデル構造のための引数
-
pedigree:- 血縁行列(A行列)の逆行列を作成するための血統情報を含むデータフレームです。アニマルモデル等の遺伝解析で使用します。
-
ginverse:- ユーザーが定義した逆行列(A逆行列など)をリスト形式で渡します。
pedigree引数を使わずに直接行列を渡す場合に用います。
- ユーザーが定義した逆行列(A逆行列など)をリスト形式で渡します。
-
nodes:- 血統情報の処理において、どの個体を含めるかを指定します(
"ALL","FIT","PRUNE")。
- 血統情報の処理において、どの個体を含めるかを指定します(
-
scale:-
pedigree使用時に血縁行列をスケーリングするかどうかの論理値です。
-
出力・保存・その他の設定引数
-
pr:- 変量効果の事後分布(BLUPsのような個別の効果)を保存するかどうかの論理値です。
TRUEにすると、各水準の効果も出力されます。
- 変量効果の事後分布(BLUPsのような個別の効果)を保存するかどうかの論理値です。
-
pl:- 潜在変数(liability)の事後分布を保存するかどうかの論理値です。
-
verbose:- MCMCの進行状況を表示するかどうかの論理値です。
-
DIC:- Deviance Information Criterion(逸脱情報量規準)を計算するかどうかの論理値です。
-
singular.ok:- 固定効果のデザイン行列がランク落ち(特異)している場合に、逆行列計算を一般化逆行列で行いエラーを回避するかどうかの論理値です。
-
saveX,saveZ,saveXL:- デザイン行列(X, Zなど)を結果オブジェクトに保存するかどうかの論理値です。
-
slice:- スライスサンプリングを使用するかどうかの論理値です。
-
mev:- 測定誤差分散(Measurement Error Variance)が含まれている場合に、その情報を渡すためのベクトルです。
-
trunc:- 切断分布を用いる場合のパラメータですが、コード内では整数として渡されています。
シミュレーション用サンプルデータの作成と解析
本関数の挙動を確認するため、「森林生態系における樹木成長データ」を作成します。
このデータセットは、階層構造(地域 > 調査区画)を持ち、複数の説明変数(連続変数およびカテゴリカル変数)を含みます。
これにより、MCMCglmm の変量効果および固定効果の推定能力を確認します。
シナリオ設定
- 応答変数 (
TreeHeight):- 樹木の高さ(メートル)。正規分布に従うと仮定。
- 固定効果:
-
Temperature: 平均気温(連続変数)。 -
Fertilizer: 施肥の有無(2値のカテゴリカル変数: “あり”, “なし”)。
-
- 変量効果:
-
Region: 地域(上位のクラスタ)。地域ごとにベースとなる成長率が異なると仮定。 -
Plot: 各地域内の調査区画(下位のクラスタ)。区画ごとの微細環境の違い。
-
Rコードによるシミュレーション
以下に、シミュレーションおよび解析を実行するためのコードを示します。
なお、有意水準は5%とします。
サンプルデータの作成
# ライブラリの読み込み
library(ggplot2)
library(gridExtra)
# 乱数シードの設定(再現性確保のため)
seed <- 20251208
set.seed(seed)
# パラメータ設定
n_regions <- 30
n_plots_per_region <- 5 # 1地域あたりの区画数
n_trees_per_plot <- 20 # 1区画あたりの樹木数
# 総サンプルサイズ
total_obs <- n_regions * n_plots_per_region * n_trees_per_plot
# IDの生成
region_id <- rep(1:n_regions, each = n_plots_per_region * n_trees_per_plot)
# 区画IDを1から通し番号で作ることで、階層構造(地域ごとのユニークさ)を表現
plot_id <- rep(1:(n_regions * n_plots_per_region), each = n_trees_per_plot)
# 説明変数の生成
temperature <- rnorm(total_obs, mean = 15, sd = 3)
fertilizer <- sample(c("なし", "あり"), total_obs, replace = TRUE)
# 真のパラメータ(固定効果)
intercept_true <- 10.0 # 切片
beta_temp <- 0.5 # 気温の効果
beta_fert <- 2.0 # 施肥の効果
# 真の分散成分(変量効果と残差)
sigma_region <- 3.0 # 地域間の標準偏差(分散=9.0)
sigma_plot <- 1.5 # 区画間の標準偏差(分散=2.25)
sigma_resid <- 1.0 # 残差標準偏差(分散=1.0)
# 変量効果の実現値を生成
region_eff_vals <- rnorm(n_regions, 0, sigma_region)
region_effect <- region_eff_vals[region_id]
plot_eff_vals <- rnorm(n_regions * n_plots_per_region, 0, sigma_plot)
plot_effect <- plot_eff_vals[plot_id]
residuals <- rnorm(total_obs, 0, sigma_resid)
# 応答変数の生成
fert_dummy <- ifelse(fertilizer == "あり", 1, 0)
y_val <- intercept_true +
beta_temp * temperature +
beta_fert * fert_dummy +
region_effect +
plot_effect +
residuals
# データフレームの作成
forest_data <- data.frame(
TreeHeight = y_val,
Temperature = temperature,
Fertilizer = factor(fertilizer, levels = c("なし", "あり")),
Region = factor(region_id),
Plot = factor(plot_id)
)
cat("--- サンプルデータの一部を確認 ---\n")
print(str(forest_data))--- サンプルデータの一部を確認 ---
'data.frame': 3000 obs. of 5 variables:
$ TreeHeight : num 17.7 18.1 17.4 20.1 16.9 ...
$ Temperature: num 15.8 17.8 15 14.4 15.2 ...
$ Fertilizer : Factor w/ 2 levels "なし","あり": 1 1 2 2 1 2 2 1 2 1 ...
$ Region : Factor w/ 30 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 1 1 ...
$ Plot : Factor w/ 150 levels "1","2","3","4",..: 1 1 1 1 1 1 1 1 1 1 ...
NULL作成したデータセットは、地域 (Region) の中に複数の区画 (Plot) が含まれ、さらにその中に個々の樹木データが存在するという階層構造を持っています。
このようなデータに対し、通常の線形回帰(lm)を適用すると、同じ地域や区画内のデータ間の相関を無視することになり、標準誤差を過小評価する恐れがあります。
MCMCglmm によるモデル構築と推定
# 事前分布の設定(弱情報事前分布)
prior_setting <- list(
R = list(V = 1, nu = 0.002),
G = list(
G1 = list(V = 1, nu = 0.002), # Region用
G2 = list(V = 1, nu = 0.002) # Plot用
)
)
model_fit <- MCMCglmm(
fixed = TreeHeight ~ Temperature + Fertilizer,
random = ~ Region + Plot,
rcov = ~units,
family = "gaussian",
data = forest_data,
prior = prior_setting,
nitt = 30000,
burnin = 10000,
thin = 10,
verbose = FALSE
)-
fixed = TreeHeight ~ Temperature + Fertilizer:- 樹木の高さ(応答変数)が、気温と施肥の有無(固定効果)によって説明されると仮定しています。
-
random = ~ Region + Plot:- データ収集の構造に起因するランダムなばらつきとして、地域差と区画差を変量効果としてモデルに組み込みました。これにより、地域ごとのベースラインの違いや、局所的な環境の違いを考慮できます。
-
prior:- ベイズ推定における事前分布です。ここでは分散成分(RとG)に対し、逆ウィシャート分布(
Vとnuで指定)を用いた弱情報事前分布を設定しました。
- ベイズ推定における事前分布です。ここでは分散成分(RとG)に対し、逆ウィシャート分布(
結果の表示と解釈
cat("--- モデルの要約結果 ---\n")
summary(model_fit)--- モデルの要約結果 ---
Iterations = 10001:29991
Thinning interval = 10
Sample size = 2000
DIC: 8694.339
G-structure: ~Region
post.mean l-95% CI u-95% CI eff.samp
Region 8.911 4.437 14.16 2000
~Plot
post.mean l-95% CI u-95% CI eff.samp
Plot 2.518 1.871 3.164 2000
R-structure: ~units
post.mean l-95% CI u-95% CI eff.samp
units 1.011 0.9624 1.066 2000
Location effects: TreeHeight ~ Temperature + Fertilizer
post.mean l-95% CI u-95% CI eff.samp pMCMC
(Intercept) 10.2363 9.1775 11.3527 2000 <5e-04 ***
Temperature 0.5059 0.4928 0.5176 2000 <5e-04 ***
Fertilizerあり 2.0058 1.9392 2.0824 2000 <5e-04 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1MCMCサンプリングの設定 (Header Information)
- Iterations = 10001:29991:
- バーンイン(最初の10,000回)を除去した後、10,001回目から29,991回目までのサンプリングが使用されました。
- Thinning interval = 10:
- 10回に1回の割合でサンプリングデータを記録しました(自己相関を減らすため)。
- Sample size = 2000:
- 最終的に事後分布を構成するサンプル数は2,000個です。
eff.samp(有効サンプルサイズ)が全て2000となっていることからも、サンプリング効率は良好です。
- 最終的に事後分布を構成するサンプル数は2,000個です。
- DIC: 8694.339:
- 逸脱情報量規準です。今回は単一モデルの評価ですが、他のモデルと比較する際にはこの値が小さいほど「予測精度と複雑さのバランスが良い」と判断されます。
変量効果の分散成分 (G-structure)
ここでは、変量効果(ランダム効果)の分散(Variance)が推定されています。
-
~Region(地域差の分散)- post.mean (事後平均): 8.911
- シミュレーションの真値は
sigma_region= 3.0 であったため、真の分散は \(3.0^2 = 9.0\) です。推定値 8.911 は真値に近い結果が得られています。
- シミュレーションの真値は
- 95% CI (信用区間): 4.437 - 14.16
- 上位階層の分散推定は不確実性が大きくなりやすいため信用区間は広めですが、区間内に真値 9.0 が含まれています。
- post.mean (事後平均): 8.911
-
~Plot(区画差の分散)- post.mean: 2.518
- シミュレーションの真値は
sigma_plot= 1.5 であったため、真の分散は \(1.5^2 = 2.25\) となり、近い値が推定できています。
- シミュレーションの真値は
- 95% CI: 1.871 - 3.164
- こちらの区間内にも真値 2.25 が含まれています。
- post.mean: 2.518
残差の分散成分 (R-structure)
-
~units(個体ごとの残差分散)- post.mean: 1.011
- シミュレーションの真値は
sigma_resid= 1.0 であったため、真の分散は \(1.0^2 = 1.0\) と、ほぼ真値を推定できています。これは最下層(個体レベル)のサンプルサイズ(総数3000)が大きいことも一因です。
- シミュレーションの真値は
- post.mean: 1.011
固定効果の推定 (Location effects)
ここでは、回帰係数の推定結果が示されています。
-
(Intercept)(切片)- post.mean: 10.2363
- 真値 10.0 に対し、近い値が推定されています。95%信用区間(9.17 - 11.35)も真値を含んでいます。
- post.mean: 10.2363
-
Temperature(気温の効果)- post.mean: 0.5059
- 真値 0.5 に対し、近い値が推定されています。
- pMCMC: <5e-04 ***
- ベイズ的なp値(パラメータが0をまたぐ確率などから算出)が小さく、統計的に有意であることが示されています。
- post.mean: 0.5059
-
Fertilizerあり(施肥の効果)- post.mean: 2.0058
- 真値 2.0 に対し、こちらも近い推定値です。施肥によって樹高が約2メートル高くなるという効果を検出しています。
- post.mean: 2.0058
cat("--- 真の値と推定値(事後平均)の比較 ---\n")
# 結果抽出
fixed_means <- summary(model_fit)$solutions[, "post.mean"]
random_vars <- summary(model_fit)$Gcovariances[, "post.mean"]
resid_var_val <- summary(model_fit)$Rcovariances[, "post.mean"]
# 固定効果の表示
cat(sprintf("切片 (真値: %.1f): 推定値 %.3f\n", intercept_true, fixed_means["(Intercept)"]))
cat(sprintf("気温効果 (真値: %.1f): 推定値 %.3f\n", beta_temp, fixed_means["Temperature"]))
cat(sprintf("施肥効果 (真値: %.1f): 推定値 %.3f\n", beta_fert, fixed_means["Fertilizerあり"]))
# 分散成分の表示
# random_varsベクトルから名前で安全に取り出すか、順序が既知ならインデックスを使う
# MCMCglmmの出力順序は formula の random 指定順 (Region, Plot)
cat("\n\n--- 分散成分の比較(分散 = 標準偏差^2) ---\n")
cat(sprintf("地域分散 (真値: %.2f): 推定値 %.3f\n", sigma_region^2, random_vars[1])) # Region
cat(sprintf("区画分散 (真値: %.2f): 推定値 %.3f\n", sigma_plot^2, random_vars[2])) # Plot
# 残差分散(最初の要素を取得)
cat(sprintf("残差分散 (真値: %.2f): 推定値 %.3f\n", sigma_resid^2, resid_var_val[1]))--- 真の値と推定値(事後平均)の比較 ---
切片 (真値: 10.0): 推定値 10.236
気温効果 (真値: 0.5): 推定値 0.506
施肥効果 (真値: 2.0): 推定値 2.006
--- 分散成分の比較(分散 = 標準偏差^2) ---
地域分散 (真値: 9.00): 推定値 8.911
区画分散 (真値: 2.25): 推定値 2.518
残差分散 (真値: 1.00): 推定値 1.011診断プロットの作成
# データフレーム化
df_sol <- data.frame(model_fit$Sol)
df_vcov <- data.frame(model_fit$VCV)
# 気温係数のトレースプロット
p1 <- ggplot(df_sol, aes(x = seq_along(Temperature), y = Temperature)) +
geom_line(color = "blue", alpha = 0.6) +
labs(title = "気温係数のトレースプロット", x = "イテレーション", y = "推定値") +
theme_minimal()
# 気温係数の事後分布密度
p2 <- ggplot(df_sol, aes(x = Temperature)) +
geom_density(fill = "orange", alpha = 0.4) +
geom_vline(xintercept = beta_temp, color = "red", linetype = "dashed", size = 1) +
labs(title = "気温係数の事後分布密度", x = "推定値", y = "密度") +
annotate("text", x = beta_temp, y = 0, label = "真の値", vjust = -1, color = "red") +
theme_minimal()
# 地域分散のトレースプロット
p3 <- ggplot(df_vcov, aes(x = seq_along(Region), y = Region)) +
geom_line(color = "darkgreen", alpha = 0.6) +
labs(title = "地域分散のトレースプロット", x = "イテレーション", y = "分散推定値") +
theme_minimal()
# 地域分散の事後分布密度
p4 <- ggplot(df_vcov, aes(x = Region)) +
geom_density(fill = "lightgreen", alpha = 0.4) +
geom_vline(xintercept = sigma_region^2, color = "red", linetype = "dashed", size = 1) +
labs(title = "地域分散の事後分布密度", x = "分散推定値", y = "密度") +
theme_minimal()
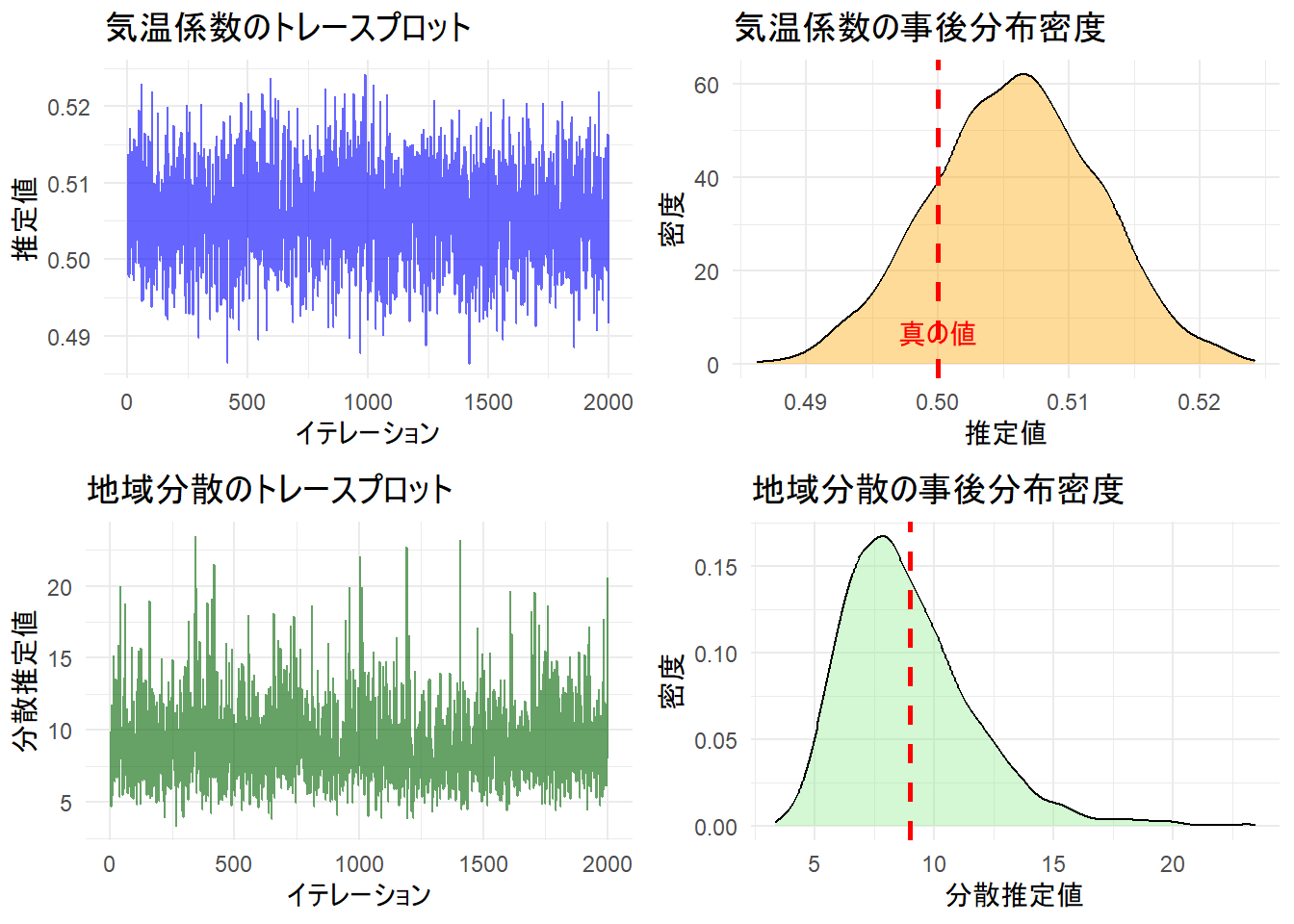
# プロットの描画
grid.arrange(p1, p2, p3, p4, ncol = 2)以上です。