Rの関数から cell2nb {spdep} を確認します。
本ポストはこちらの続きです。

関数 cell2nb とは
cell2nb (Cell to Neighbors) は、規則的な格子状(グリッド)の空間構造において、近傍リスト(neighbors list, nb クラスのオブジェクト)を作成するための関数です。
地理空間データ分析において、メッシュデータやラスタデータのような正則格子データを扱う際、「どのセルとどのセルが隣接しているか」を定義する必要があります。
cell2nb は、行数と列数を指定するだけで、この隣接関係を自動的に生成します。
隣接の定義には、チェスの駒の動きになぞらえた「ルーク型(Rook: 上下左右)」と「クイーン型(Queen: 全8方向)」を選択可能です。
関数 cell2nb の引数
library(spdep)
args(cell2nb)function (nrow, ncol, type = "rook", torus = FALSE, legacy = FALSE,
x = NULL)
NULL- nrow
- グリッドの行数(整数の数値)。
- 空間格子の縦方向のサイズを決定します。
- 第1引数に数値ではなく
SpatialGridやGridTopologyオブジェクトが渡された場合、関数内部で自動的に行数・列数が抽出され、変数xとして処理されます。
- ncol
- グリッドの列数(整数の数値)。
- 空間格子の横方向のサイズを決定します。
nrowとncolの積が全セル数(\(n\))となります。
- type
- 隣接関係の定義タイプを指定する文字列。デフォルトは
"rook"です。 - どのような位置関係にあるセルを「隣接」とみなすかを決定します。
-
"rook"(ルーク): 上下左右の4方向のみを隣接とみなします(共有する辺がある場合)。 -
"queen"(クイーン): 上下左右に加え、斜めの4方向も隣接とみなします(共有する点または辺がある場合)。
-
- 隣接関係の定義タイプを指定する文字列。デフォルトは
- torus
- 空間をトーラス(ドーナツ型)構造として扱うかを指定する論理値。デフォルトは
FALSEです。 - グリッドの端の処理を決定します。
-
FALSE: 平面として扱い、端にあるセルは外側との隣接を持ちません(近傍数が少なくなります)。 -
TRUE: 右端と左端、上端と下端がつながっているとみなします。すべてのセルが等しい近傍数を持ちます。
-
- 空間をトーラス(ドーナツ型)構造として扱うかを指定する論理値。デフォルトは
- legacy
- 古いバージョンの座標順序(IDの割り当て順)を使用するかを指定する論理値。デフォルトは
FALSEです。 - 過去の分析結果との互換性を保つために存在します。行と列のループ順序が異なります。
- 古いバージョンの座標順序(IDの割り当て順)を使用するかを指定する論理値。デフォルトは
- x
- 内部処理用の引数、またはグリッドオブジェクト自体。
-
nrowの位置にSpatialGridオブジェクトなどが渡された場合、当該オブジェクトがxに格納され、そこからnrowとncolが抽出されます。
シミュレーション用サンプルデータとコード
cell2nb の挙動、特に type="rook" と type="queen" の違い、および torus の効果を視覚的に確認するため、小規模な \(5 \times 5\) のグリッドを用いたシミュレーションを行います。
サンプルデータの作成 (5x5 グリッドの座標)
rows と cols を指定して、 \(5 \times 5\) の仮想的な座標点 coords を生成します。
cell2nb 関数自体は座標データを必要としませんが、結果を plot 関数で可視化する際に、各ノード(セル)をどこに配置するかを指定するために使用します。
# cell2nb自体はデータフレームを必要としませんが、
# 可視化のために各セルの中心座標を作成します。
rows <- 5
cols <- 5
n_cells <- rows * cols
# グリッドの座標を作成 (1:5 の範囲で xy座標を生成)
# spdepの並び順に合わせて座標を生成します (左上から右下へ、あるいは左下から右上へ)
# 通常、cell2nbは行(row)優先でIDを振りますが、可視化の際はexpand.gridで対応します
coords <- expand.grid(x = 1:cols, y = rows:1) # yは上から下へ描画されるよう反転
cat("--- 作成したグリッド座標の構造を確認 ---\n")
print(str(coords))--- 作成したグリッド座標の構造を確認 ---
'data.frame': 25 obs. of 2 variables:
$ x: int 1 2 3 4 5 1 2 3 4 5 ...
$ y: int 5 5 5 5 5 4 4 4 4 4 ...
- attr(*, "out.attrs")=List of 2
..$ dim : Named int [1:2] 5 5
.. ..- attr(*, "names")= chr [1:2] "x" "y"
..$ dimnames:List of 2
.. ..$ x: chr [1:5] "x=1" "x=2" "x=3" "x=4" ...
.. ..$ y: chr [1:5] "y=5" "y=4" "y=3" "y=2" ...
NULL cell2nb による近傍リストの作成
- Rook型: 上下左右の隣接のみをリンクとして生成します。
- Queen型: 斜めの隣接もリンクとして生成します。
- Torus (トーラス):
type="rook"ですがtorus=TRUEとすることで、グリッドの左端と右端、上端と下端がつながるように設定します。
# (A) Rook型 (上下左右)
nb_rook <- cell2nb(nrow = rows, ncol = cols, type = "rook")
# (B) Queen型 (上下左右 + 斜め)
nb_queen <- cell2nb(nrow = rows, ncol = cols, type = "queen")
# (C) Rook型 + トーラス構造 (端同士がつながる)
nb_torus <- cell2nb(nrow = rows, ncol = cols, type = "rook", torus = TRUE)
cat("--- (A) Rook型 (上下左右) ---\n")
nb_rook
cat("\n--- (B) Queen型 (上下左右 + 斜め) ---\n")
nb_queen
cat("\n--- (C) Rook型 + トーラス構造 (端同士がつながる) ---\n")
nb_torus--- (A) Rook型 (上下左右) ---
Neighbour list object:
Number of regions: 25
Number of nonzero links: 80
Percentage nonzero weights: 12.8
Average number of links: 3.2
--- (B) Queen型 (上下左右 + 斜め) ---
Neighbour list object:
Number of regions: 25
Number of nonzero links: 144
Percentage nonzero weights: 23.04
Average number of links: 5.76
--- (C) Rook型 + トーラス構造 (端同士がつながる) ---
Neighbour list object:
Number of regions: 25
Number of nonzero links: 100
Percentage nonzero weights: 16
Average number of links: 4 3種類の近傍定義(Rook, Queen, Torus)によって、空間的なつながりの強さ(リンク数)がどのように変化するかを定量的に確認できます。
共通事項として、Number of regions: 25 は、\(5 \times 5\) のグリッド(全25セル)が正しく認識されていることを表しています。
nb_rook (通常のルーク型)
Number of nonzero links: 80
Average number of links: 3.2 上下左右のみを隣接とみなす定義です。
本来、グリッドの内側にあるセルは4つの近傍を持ちますが、端(エッジ)や角(コーナー)にあるセルは外側との接点を持たないため、近傍数が減少し(3つまたは2つになり)ます。
具体的には、内側9セル(\(\times 4\))、辺上の12セル(\(\times 3\))、角の4セル(\(\times 2\))の合計でリンク総数は80となります。
それゆえ、平均リンク数は4を下回る 3.2 となっています。当該数値は「境界効果(端の影響)」が強く表れていることを示唆します。
nb_queen (クイーン型)
Number of nonzero links: 144
Average number of links: 5.76 上下左右に加え、斜め方向も隣接とみなす定義です。
内側のセルは最大で8つの近傍を持つことになります。その結果、リンク総数は 144 へと増加しました。
Rook型と比較してネットワークの密度(Percentage nonzero weights)が 12.8% から 23.04% へと上昇しており、情報の波及経路がより密に張り巡らされていることが分かります。
nb_torus (トーラス構造)
Number of nonzero links: 100
Average number of links: 4 Rook型に「端同士をつなげる」処理を加えた定義です。
通常であれば近傍数が減ってしまう端や角のセルが、反対側のセルと接続されることで、全てのセルが平等に「4つ」の近傍を持つことになります。
そのため、リンク総数は \(25 \text{セル} \times 4 = 100\) となり、平均リンク数も 4 となっています。
空間的な「端」の存在がノイズとなることを防ぎたい場合に、このトーラス構造が有効であることが数値からも読み取れます。
まとめ
- nb_rook: シンプルだが、端の影響で平均近傍数が下がる。
- nb_queen: 斜めを含むため、つながりが多くなる。
- nb_torus: 端の影響を排除し、全てのセルで均一なつながり(近傍数4)を保つ。
構造の違いを確認する
具体的に、2つのセル(ID=13とID=1)の近傍数を確認します。
前述のとおり、
- Rook型: 中心のセルは4つの近傍を持ちますが、角(コーナー)のセルは2つしか近傍を持ちません。
- Queen型: 中心のセルは8つの近傍を持ち、角のセルは3つの近傍を持ちます。
- Torus: 全てのセルが平等に4つの近傍を持ちます(角のセルも反対側とつながるため)。
cat("----------------------------------------------------------------\n")
cat("【近傍定義によるリンク数の比較】\n")
cat(sprintf("グリッドサイズ: %d 行 x %d 列 (全 %d セル)\n", rows, cols, n_cells))
cat("----------------------------------------------------------------\n")
# 各近傍定義における総リンク数(双方向)を表示
# card() 関数は各領域の近傍数を返します。その総和がリンクの総数(片方向)です。
cat(sprintf("(A) Rook型 (上下左右) の総リンク数: %d\n", sum(card(nb_rook))))
cat(sprintf("(B) Queen型 (全8方向) の総リンク数: %d\n", sum(card(nb_queen))))
cat(sprintf("(C) Rook型 (トーラス) の総リンク数: %d\n", sum(card(nb_torus))))
cat("\n----------------------------------------------------------------\n")
cat("【中心セルと角セルの近傍数】\n")
cat("----------------------------------------------------------------\n")
# 中心セル(ID: 13, 座標(3,3)付近)と 角セル(ID: 1, 左上)の近傍数を確認
center_id <- 13
corner_id <- 1
cat(sprintf("中心セル(ID=%d) の近傍数:\n", center_id))
cat(sprintf(" Rook : %d (上下左右)\n", card(nb_rook)[center_id]))
cat(sprintf(" Queen: %d (斜め含む)\n", card(nb_queen)[center_id]))
cat(sprintf(" Torus: %d\n", card(nb_torus)[center_id]))
cat(sprintf("\n角セル(ID=%d) の近傍数:\n", corner_id))
cat(sprintf(" Rook : %d (端なので2方向のみ)\n", card(nb_rook)[corner_id]))
cat(sprintf(" Queen: %d (端なので3方向のみ)\n", card(nb_queen)[corner_id]))
cat(sprintf(" Torus: %d (端がつながるため4方向)\n", card(nb_torus)[corner_id]))----------------------------------------------------------------
【近傍定義によるリンク数の比較】
グリッドサイズ: 5 行 x 5 列 (全 25 セル)
----------------------------------------------------------------
(A) Rook型 (上下左右) の総リンク数: 80
(B) Queen型 (全8方向) の総リンク数: 144
(C) Rook型 (トーラス) の総リンク数: 100
----------------------------------------------------------------
【中心セルと角セルの近傍数】
----------------------------------------------------------------
中心セル(ID=13) の近傍数:
Rook : 4 (上下左右)
Queen: 8 (斜め含む)
Torus: 4
角セル(ID=1) の近傍数:
Rook : 2 (端なので2方向のみ)
Queen: 3 (端なので3方向のみ)
Torus: 4 (端がつながるため4方向)可視化による比較
(注意)
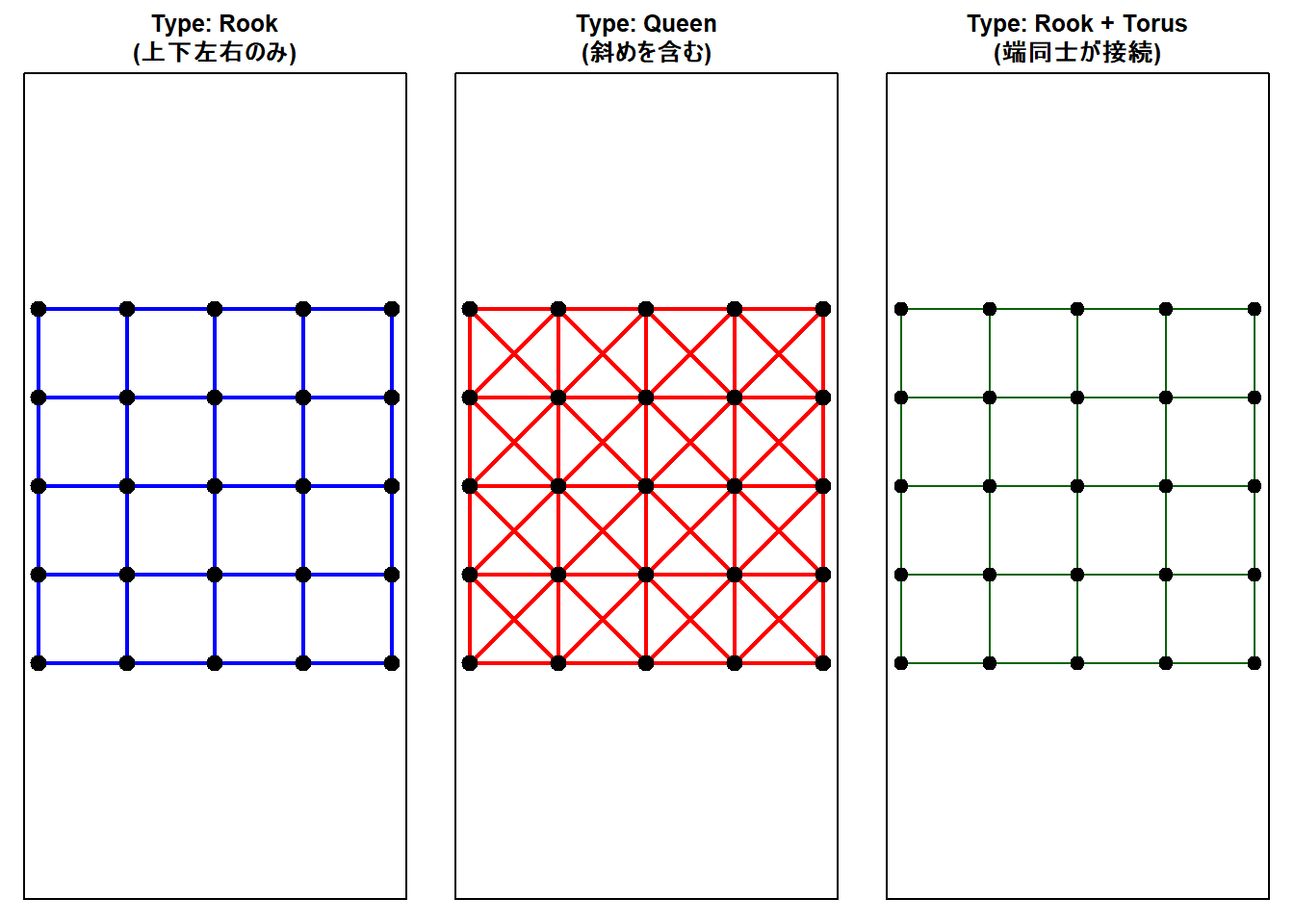
Figure 1 のとおり、「Rook」と「Rook + Torus」に視覚的な違いは見られません。
spdep パッケージの plot 関数は、隣接しているセルの中心同士を「直線」で結びます。
- 通常のRook: 隣り合うセル(例:左端と、その右隣)が結ばれます。これで格子状の線ができます。
- Torus(トーラス)の場合:
- 「左端のセル」と「右端のセル」が隣接しているとみなされます。
- この2つを結ぶ線を引こうとすると、「左端から右端へ向かう一直線」が描かれます。
- この直線は、既存のグリッドの横線(左→中央→右)と完全に重なってしまいます。
- 縦方向(上端と下端の接続)も同様に、既存の縦線の上に長い直線が重なって描画されます。
その結果、「線は描かれているが、既存の線の下(または上)に隠れてしまって見えない」というプロットになります。
# 画面を3分割してプロット
par(mfrow = c(1, 3), mar = c(1, 1, 3, 1))
# (A) Rook Plot
plot(nb_rook, coords, col = "blue", pch = 19, cex = 1.5, lwd = 2)
title(main = "Type: Rook\n(上下左右のみ)")
box()
# (B) Queen Plot
plot(nb_queen, coords, col = "red", pch = 19, cex = 1.5, lwd = 2)
title(main = "Type: Queen\n(斜めを含む)")
box()
# (C) Torus Plot (Rook)
plot(nb_torus, coords, col = "darkgreen", pch = 19, cex = 1.5, lwd = 1)
title(main = "Type: Rook + Torus\n(端同士が接続)")
box()# 左上の角にあるセル(ID: 1)の隣接状況を確認
cat("----------------------------------------------------------------\n")
cat("【左上角セル (ID=1) の隣接リスト確認】\n")
cat("----------------------------------------------------------------\n")
# (A) 通常のRook
# 端なので、右(2)と下(6)の2つだけ
cat("(A) Rook型 の隣接ID:\n")
print(nb_rook[[1]])
# (C) Rook + Torus型
# 右(2)と下(6)に加え、
# 左につながる「右端(5)」と、上につながる「下端(21)」が含まれています
cat("\n(C) Rook + Torus型 の隣接ID:\n")
print(nb_torus[[1]])
cat("----------------------------------------------------------------\n")
cat("Torus型では、ID:1 の隣接に '5' (右端) と '21' (下端) が追加されています。\n")
cat("この '1' と '5' を結ぶ線が、1-2-3-4-5 のグリッド線と重なって描画されています。\n")
cat("----------------------------------------------------------------\n")----------------------------------------------------------------
【左上角セル (ID=1) の隣接リスト確認】
----------------------------------------------------------------
(A) Rook型 の隣接ID:
[1] 2 6
(C) Rook + Torus型 の隣接ID:
[1] 2 5 6 21
----------------------------------------------------------------
Torus型では、ID:1 の隣接に '5' (右端) と '21' (下端) が追加されています。
この '1' と '5' を結ぶ線が、1-2-3-4-5 のグリッド線と重なって描画されています。
----------------------------------------------------------------以上です。