Rの関数:mk.test {trend}

関数 mk.test とは

関数 mk.test は、時系列データに対して Mann-Kendall（マン・ケンドール）検定 を実行するための関数です。

Mann-Kendall 検定は、データ系列に 「単調な（monotonic）トレンド」 が存在するかどうかを評価するノンパラメトリック検定です。

この検定の特長は、データが特定の分布（正規分布など）に従うことを仮定しない点、および外れ値の影響を受けにくい点にあります。

線形トレンドだけでなく、非線形であっても単調に増加、あるいは減少している傾向を検出することができます。

帰無仮説（\(H_0\)）は「トレンドが存在しない（データはランダムに並んでいる）」であり、対立仮説（\(H_1\)）は「単調なトレンドが存在する」となります。

関数 mk.test の引数

library(trend)
args(mk.test)

function (x, alternative = c("two.sided", "greater", "less"), 
    continuity = TRUE) 
NULL

1. x
   • 検定対象となる数値ベクトル（numeric vector）です。通常は等間隔で測定された時系列データを渡します。
   • 数値型であり、少なくとも3つの要素を持つ必要があります。また、コード内の na.fail(x) により、欠損値（NA）が含まれている場合はエラーとなります。
2. alternative
   • 対立仮説の種類を指定します。
   • 選択肢:
     • "two.sided": 両側検定（デフォルト）。増加または減少のいずれかのトレンドがあるかを検定します。
     • "greater": 片側検定。増加トレンドがあるかを検定します。
     • "less": 片側検定。減少トレンドがあるかを検定します。
   • switch 関数により、算出されたZ値（標準化検定統計量）からp値を計算する際の領域決定に使用されます。
3. continuity
   • 連続性の補正（continuity correction）を行うかどうかの論理値です。
   • デフォルト: TRUE
   • Mann-Kendall 統計量 \(S\) は離散的な値をとりますが、検定統計量 \(Z\) は正規近似を用いて計算されます。離散分布を連続分布で近似する際の誤差を減らすために補正を行います。
   • コード上の処理: TRUE の場合、abs(S) - 1 のように \(S\) の絶対値から 1 を引いて（ゼロ方向へ縮小させて）から標準偏差で除算し、Z値を算出します。

コード内の主要な統計量

• S:
  • Mann-Kendall 統計量。全てのデータペア \((x_i, x_j)\) (\(i < j\)) について、大小関係の符号（\(x_j > x_i\) なら \(+1\)、\(x_j < x_i\) なら \(-1\)）を合計したものです。正の値は増加傾向、負の値は減少傾向を示唆します。
• varS:
  • 統計量 \(S\) の分散。タイ（同順位、同じ値）が存在する場合は、その影響を考慮して分散が調整されます（table(x) を利用してタイを検出しています）。
• tau:
  • ケンドールの順位相関係数（Kendall’s \(\tau\)）。\(S\) を正規化した指標であり、トレンドの強さを表します。

シミュレーションコード

以下に、mk.test の挙動を確認するためのサンプルデータを用いたシミュレーションコードを示します。

このシミュレーションでは、以下の2つのシナリオを設定し、それぞれの判定結果を確認します。

1. トレンドなし（ランダム）:
   • 平均回帰的な変動のみで、一貫した傾向がないデータ。
2. 単調増加トレンド:
   • 時間経過とともに徐々に値が上昇していくデータ。

なお、有意水準は5%とします。

シミュレーションデータの生成

# パッケージの読み込み
library(ggplot2)
library(patchwork)

# 乱数シードの固定
seed <- 20251226
set.seed(seed)

# 設定: 30年間の年次データ（例: ある観測地点の水質データなど）
years <- 1996:2025
n_years <- length(years)

# シナリオ1: トレンドなし（ランダムウォークではなく、平均周りのランダム変動）
# 平均 50, 標準偏差 10 の正規乱数
data_random <- rnorm(n_years, mean = 50, sd = 10)

# シナリオ2: 増加トレンドあり
# ベースライン + 年ごとの増加 + ランダムノイズ
# 毎年平均 0.8 ずつ上昇すると仮定
trend_component <- seq(0, by = 0.8, length.out = n_years)
data_trend <- 40 + trend_component + rnorm(n_years, mean = 0, sd = 5)

# データフレーム化
df_sim <- data.frame(
  Year = years,
  Value_Random = data_random,
  Value_Trend = data_trend
)

cat("--- データ概要 ---\n")
cat(sprintf("観測期間: %d 年間 (%d ～ %d)\n", n_years, min(years), max(years)))
cat("シナリオ1: ランダム変動（トレンドなし）\n")
cat("シナリオ2: 増加トレンド（単調増加）\n\n")

# データの可視化
# シナリオ1のプロット
p1 <- ggplot(df_sim, aes(x = Year, y = Value_Random)) +
  geom_line(color = "gray50") +
  geom_point(color = "blue", size = 2) +
  labs(
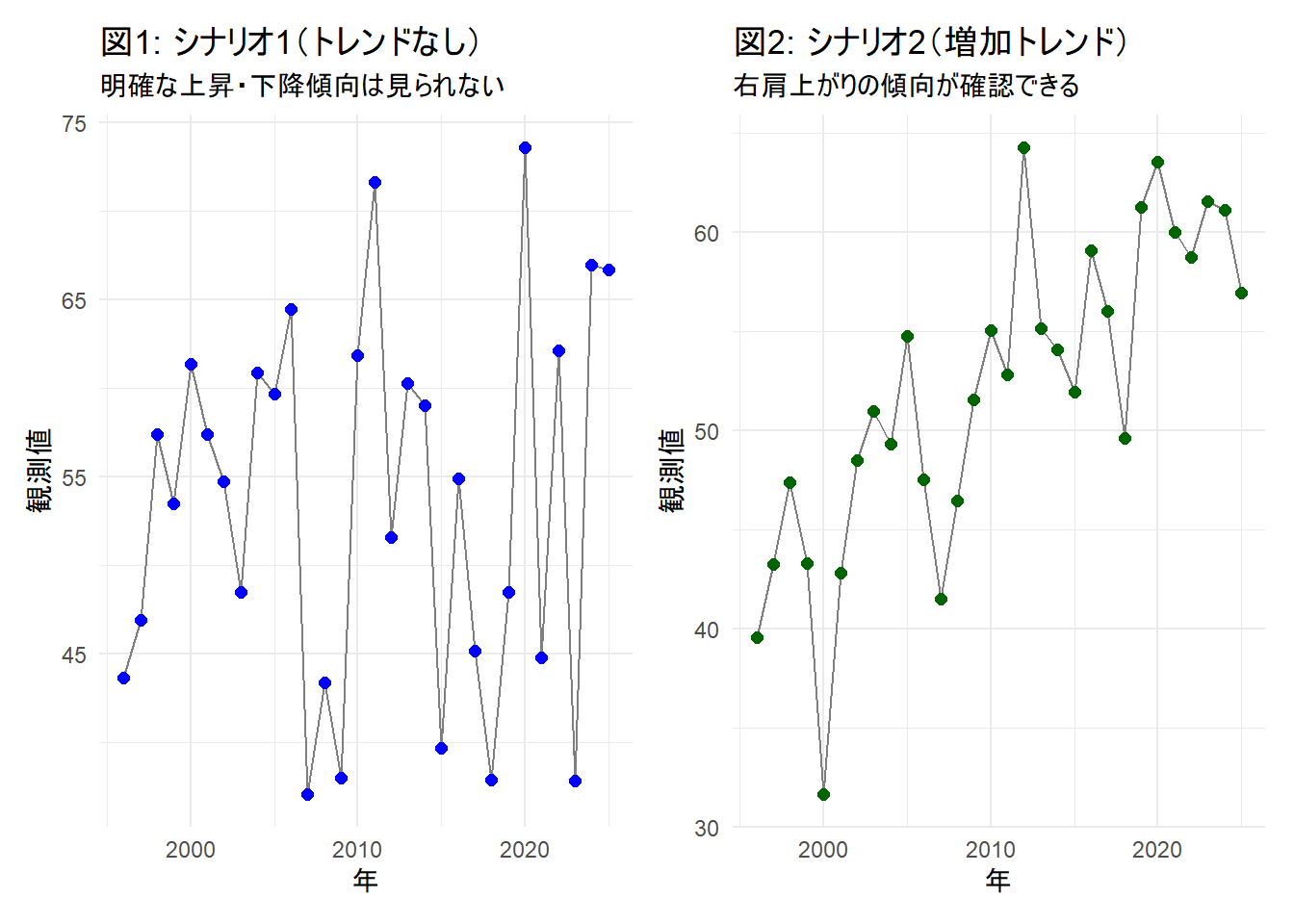
    title = "図1: シナリオ1（トレンドなし）",
    subtitle = "明確な上昇・下降傾向は見られない",
    x = "年",
    y = "観測値"
  ) +
  theme_minimal()

# シナリオ2のプロット
p2 <- ggplot(df_sim, aes(x = Year, y = Value_Trend)) +
  geom_line(color = "gray50") +
  geom_point(color = "darkgreen", size = 2) +
  labs(
    title = "図2: シナリオ2（増加トレンド）",
    subtitle = "右肩上がりの傾向が確認できる",
    x = "年",
    y = "観測値"
  ) +
  theme_minimal()

# 2つの図を並べて表示
print(p1 + p2)

--- データ概要 ---
観測期間: 30 年間 (1996 ～ 2025)
シナリオ1: ランダム変動（トレンドなし）
シナリオ2: 増加トレンド（単調増加）

# 関数 mk.test を適用

# ケース1: トレンドなしデータに対する検定
mk_res_random <- mk.test(df_sim$Value_Random, alternative = "two.sided")

# ケース2: 増加トレンドデータに対する検定
mk_res_trend <- mk.test(df_sim$Value_Trend, alternative = "two.sided")

# 結果の表示
cat("--- シナリオ1: トレンドなしデータに対する検定 ---\n")
print(mk_res_random)
cat("\n--- シナリオ2: 増加トレンドデータに対する検定 ---\n")
print(mk_res_trend)

--- シナリオ1: トレンドなしデータに対する検定 ---

    Mann-Kendall trend test

data:  df_sim$Value_Random
z = 0.53523, n = 30, p-value = 0.5925
alternative hypothesis: true S is not equal to 0
sample estimates:
           S         varS          tau 
3.100000e+01 3.141667e+03 7.126437e-02 


--- シナリオ2: 増加トレンドデータに対する検定 ---

    Mann-Kendall trend test

data:  df_sim$Value_Trend
z = 4.8884, n = 30, p-value = 1.016e-06
alternative hypothesis: true S is not equal to 0
sample estimates:
           S         varS          tau 
 275.0000000 3141.6666667    0.6321839