Rの関数から qmvt {mvtnorm} を確認します。
関数 qmvt とは
qmvt は、多変量t分布(Multivariate t-Distribution)の分位点(Quantile) を計算する関数です。
分布関数(累積確率)を \(F(x)\) としたとき、確率 \(p\) を与えて \(F(q) = p\) となる \(q\) を求める操作を「分位点を求める」と呼ばれます。
qmvt は、指定された相関構造や自由度を持つ多変量t分布において、指定された確率 \(p\) に対応する分位点(境界値、クリティカル・バリュー)を算出します。
分位点、多重比較検定(Dunnett検定など)における棄却限界値の算出や、同時信頼区間の幅を決定する際に利用されます。
qmvt は、累積分布関数である pmvt の値が \(p\) になるような点を、数値的な求根探索アルゴリズム(root-finding algorithm)を用いて探索しています。
関数 qmvt の引数
library(mvtnorm)
args(qmvt)function (p, interval = NULL, tail = c("lower.tail", "upper.tail",
"both.tails"), df = 1, delta = 0, corr = NULL, sigma = NULL,
algorithm = GenzBretz(), type = c("Kshirsagar", "shifted"),
ptol = 0.001, maxiter = 500, trace = FALSE, seed = NULL,
...)
NULL-
p- 求めたい分位点に対応する確率です。
0から1の間の数値を指定します(例: 0.95)。
- 求めたい分位点に対応する確率です。
-
interval- 解(分位点)が存在すると予想される区間を指定するベクトル
c(min, max)です。 - デフォルト:
NULL(自動的に区間が設定されます)。 - 求根探索の範囲を限定し、計算を効率化または安定化させるために用います。
- 解(分位点)が存在すると予想される区間を指定するベクトル
-
tail- 確率 \(p\) が定義される積分領域(裾)のタイプを指定します。
- 選択肢:
-
"both.tails":- 両側領域。原点を中心とした矩形領域 \([-q, q]\) (相関行列の次元数分)の確率が \(p\) となる \(q\) を求めます。同時信頼区間の計算などで利用されます。
-
"lower.tail":- 下側領域。\((-\infty, q]\) の確率が \(p\) となる \(q\) を求めます。
-
"upper.tail":- 上側領域。\([q, \infty)\) の確率が \(p\) となる \(q\) を求めます。
-
-
df- 自由度(Degrees of Freedom)を指定する整数またはベクトルです。
- デフォルト:
1 - t分布の裾の厚さを決定します。値が大きいほど正規分布に近づきます。
-
delta- 非心パラメータ(Non-centrality parameter)のベクトルです。
- デフォルト:
0(中心t分布)。 - 非心t分布を扱う場合に、分布の中心位置のズレを指定します。
-
corr- 相関行列(Correlation Matrix)です。
- 対角成分が1の対称行列である必要があります。
sigmaが指定されていない場合、こちらを指定する必要があります。
-
sigma- 分散共分散行列(Covariance Matrix)です。
- 変数間のスケールと相関を同時に定義します。関数内部で相関行列とスケールに変換されます。一変量の場合以外は、通常対角成分が1(相関行列)になるようにスケーリングして利用されます。
-
algorithm- 多変量t分布の確率密度を積分するための数値計算アルゴリズムを指定します。
- デフォルト:
GenzBretz()(準モンテカルロ法の一種)。 - 多変量積分の計算は解析的に解けないため、乱数を用いた近似計算が行われます。
-
type- 非心t分布の定義タイプを指定します。
- 選択肢:
"Kshirsagar"または"shifted"。
-
ptol- 求根探索における確率の許容誤差(tolerance)です。
- デフォルト:
0.001 - 計算された確率と目標確率 \(p\) との差がこの値以下になれば、計算を終了します。
-
maxiter- 求根探索の最大反復回数です。
- デフォルト:
500
-
trace- 計算過程(反復状況)をコンソールに表示するかどうかの論理値です。
-
seed- 乱数シード値です。
-
algorithmでモンテカルロ法が使用されるため、結果の再現性を担保するために指定します。
シミュレーションコード
以下に、qmvt の機能を確認するためのシミュレーションコードを示します。
このシミュレーションでは、「2つの相関する変数(2変量t分布)において、95%の確率で値が含まれる正方形の領域(同時信頼区間)」 の境界値を qmvt で求めます。
そして、その境界値が正しいことを、確率計算関数 pmvt および可視化によって検証します。
多変量t分布の分位点計算シミュレーション
# パッケージの読み込み
library(ggplot2)
library(gridExtra) # グラフ配置用
# 乱数シードの固定(再現性のため)
seed <- 20260107
set.seed(seed)
# 1. パラメータの設定
# 次元数: 2 (可視化しやすいため)
# 自由度 (df): 5 (裾が厚い設定)
# 相関行列: 2つの変数は 0.6 の正の相関を持つ
target_df <- 5
target_corr <- matrix(c(1, 0.6, 0.6, 1), nrow = 2)
target_prob <- 0.95 # 求めたい確率 (95%)
cat("--- 設定パラメータ ---\n")
cat(sprintf("次元数: 2\n"))
cat(sprintf("自由度: %d\n", target_df))
cat(sprintf("目標確率: %.2f (95%%)\n", target_prob))
cat("相関行列:\n")
print(target_corr)--- 設定パラメータ ---
次元数: 2
自由度: 5
目標確率: 0.95 (95%)
相関行列:
[,1] [,2]
[1,] 1.0 0.6
[2,] 0.6 1.0qmvt の実行
# 2. qmvt を用いた分位点(クリティカル値)の計算
# tail = "both.tails" を指定することで、原点を中心とした
# 矩形領域 [-q, q] x [-q, q] の確率が 0.95 になる q を求める
# seedを指定して計算結果を安定させる
q_res <- qmvt(
p = target_prob,
df = target_df,
corr = target_corr,
tail = "both.tails",
seed = seed
)
critical_value <- q_res$quantile
estimated_prob <- q_res$f.quantile + target_prob # 結果には誤差分が含まれるため補正して表示
cat("--- 結果の確認 ---\n")
cat(sprintf("計算された分位点 (q): %.4f\n", critical_value))
cat(sprintf("収束した確率値 : %.4f\n\n", estimated_prob))
cat("--- 結果の解釈 ---\n")
cat(sprintf("この結果は、自由度5、相関0.6の2変量t分布において、各変数が [%.4f, %.4f] の範囲に同時に収まる確率が約95%%であることを意味します。", -critical_value, critical_value))--- 結果の確認 ---
計算された分位点 (q): 2.9997
収束した確率値 : 0.9500
--- 結果の解釈 ---
この結果は、自由度5、相関0.6の2変量t分布において、各変数が [-2.9997, 2.9997] の範囲に同時に収まる確率が約95%であることを意味します。pmvt による検算
# 3. pmvt を用いた検算
# 求まった q を使って、本当に確率が 0.95 になるかを確認する
p_check <- pmvt(
lower = rep(-critical_value, 2),
upper = rep(critical_value, 2),
df = target_df,
corr = target_corr
)
cat(sprintf("pmvtで計算した確率: %.4f\n", p_check[1]))pmvtで計算した確率: 0.9500qmvt の結果と一致していることが確認できました。
可視化による確認
# 4. 可視化による確認
# 2変量t分布の等高線プロットを作成し、qmvtで求めた領域を図示する
# グリッドデータの作成
x_seq <- seq(-4, 4, length.out = 100)
y_seq <- seq(-4, 4, length.out = 100)
grid_data <- expand.grid(X = x_seq, Y = y_seq)
# 各グリッド点での確率密度を計算 (dmvtを使用)
grid_data$Density <- dmvt(
x = cbind(grid_data$X, grid_data$Y),
df = target_df,
sigma = target_corr,
log = FALSE
)
# プロットの作成
p1 <- ggplot(grid_data, aes(x = X, y = Y)) +
# 等高線の描画
geom_contour_filled(aes(z = Density), alpha = 0.8) +
# qmvtで求めた領域(正方形)の描画
geom_rect(
aes(
xmin = -critical_value, xmax = critical_value,
ymin = -critical_value, ymax = critical_value
),
fill = NA, color = "red", linewidth = 1.5, linetype = "dashed"
) +
# 装飾
labs(
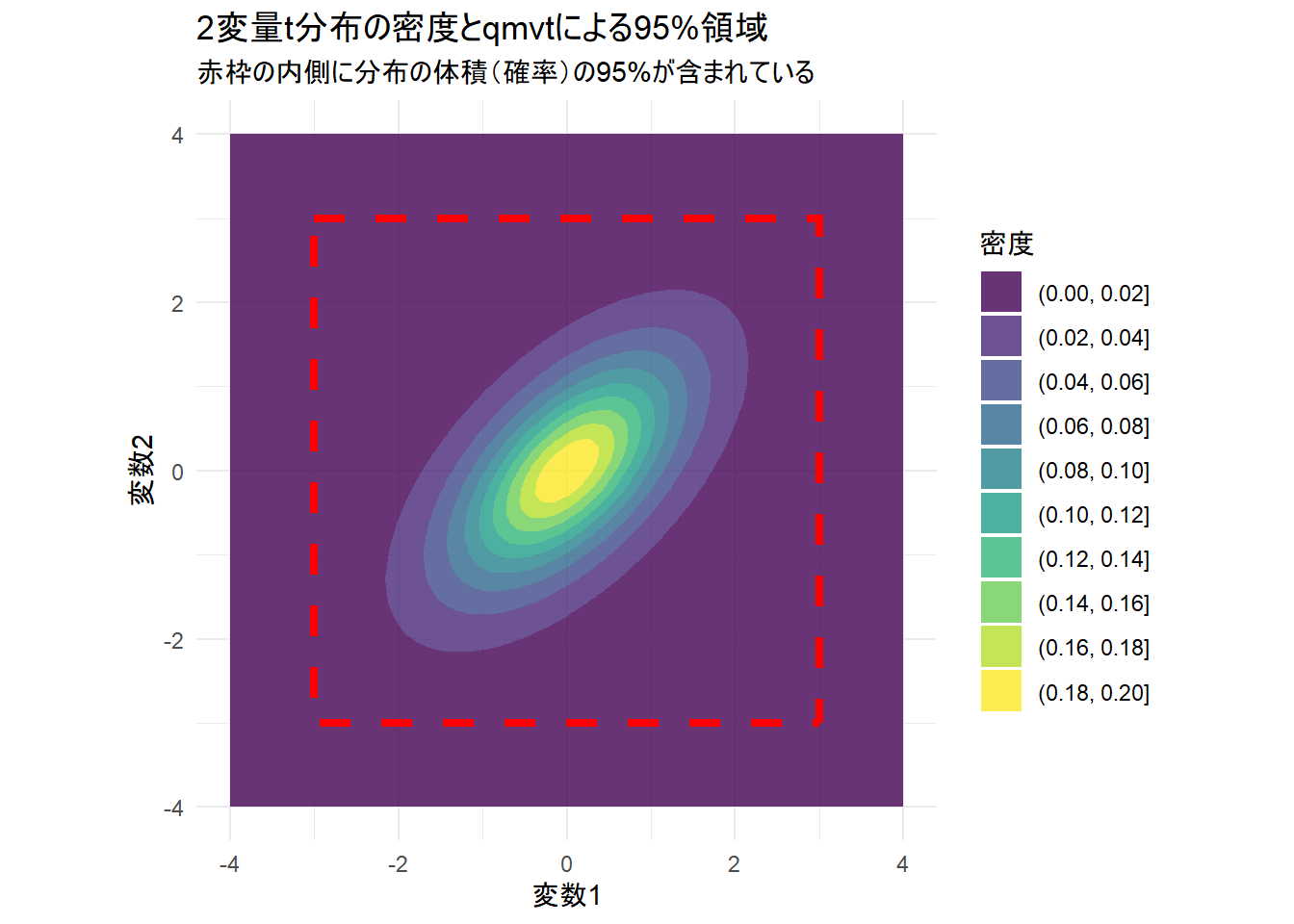
title = "2変量t分布の密度とqmvtによる95%領域",
subtitle = "赤枠の内側に分布の体積(確率)の95%が含まれている",
x = "変数1",
y = "変数2",
fill = "密度"
) +
theme_minimal() +
coord_fixed() # アスペクト比を固定
print(p1)Figure 1 は、「相関を持つ多変量データにおいて、複数の変数が同時にある範囲内に収まる確率を制御するには、どのような閾値を設定すればよいか」という問いに対する qmvt の結果を可視化しています。
分布の形状
Figure 1 の背景のグラデーションは、2変量t分布の確率密度を表しています。
- 色:
- 黄色の中心部分が最も確率密度が高く、外側の紫色の領域に行くほど密度が低くなります。
- 形状:
- 真円ではなく、右上がりの楕円形をしています。これは、シミュレーション設定で2つの変数の間に 「0.6 の正の相関」 を持たせたためです。「変数1が大きければ、変数2も大きくなりやすい」という関係性が、この傾きとして現れています。
赤い破線の正方形(qmvtの計算結果)
Figure 1 赤い枠は、関数 qmvt が計算した「同時信頼区間(Simultaneous Confidence Region)」の境界線です。
- 枠の意味:
- この正方形の領域(\(-q \le X \le q\) かつ \(-q \le Y \le q\))の内側に、分布全体の体積(確率)のちょうど 95% が含まれるように計算されています。
- 正方形である理由:
- 引数
tail = "both.tails"を指定したため、各変数に対して原点から等距離の対称な境界値(\(|x| < q\))が適用され、結果として正方形の領域となります。
- 引数
統計的な示唆
- もし、この分布からランダムに点を1つ打った場合、その点が「赤い枠の中に落ちる確率は95%」であり、「枠の外に外れる確率は5%」です。
- Figure 1 の赤い枠は個別のt分布の95%点(1変量での計算)よりも少し大きく(広く)なっています。2つの変数を同時に判定する場合、「どちらか片方でも外れたらアウト」となるため、全体の成功確率を95%に保つには、個別の基準を厳しく(枠を広く)する必要があるためです。
以上です。