Rの関数 qmvt {mvtnorm} を利用して、ガブリエル比較区間を算出します。
本ポストはこちらの続きです。

ガブリエル比較区間とは
多重比較(ANOVA後の検定など)において、「どの群とどの群に差があるか」を視覚的に判定するための手法です。
- 通常の95%信頼区間:
- 区間が重なっていても、有意差がある場合がある(「重なり」=「差がない」とは限らない)。
- ガブリエル区間:
- 「区間が重ならない \(\iff\) 統計的に有意差がある」 となるように設計された区間。
この区間の計算には、スチューデント化最大絶対値分布(SMM: Studentized Maximum Modulus distribution)の分位点が必要であり、ここで qmvt を利用します。
シミュレーションの設計
- データ生成:
- 3つのグループ(A, B, C)を作成します。
- グループAとBの間には、「通常の信頼区間なら重なって見えるが、実際には有意差がある」という微妙な差を設定します。
- qmvtの利用:
- SMM分布のクリティカル・バリューを
qmvtで計算します(相関行列を単位行列に設定することでSMMを再現できます)。
- SMM分布のクリティカル・バリューを
- 可視化:
- 通常の信頼区間(重なる)と、ガブリエル区間(重ならない)を並べてプロットし、判定のしやすさを比較します。
ガブリエル比較区間のシミュレーション
# パッケージの読み込み
library(mvtnorm)
library(ggplot2)
library(dplyr)
# 乱数シードの固定
seed <- 20260108
set.seed(seed)
# 1. サンプルデータの生成
# 3つのグループを作成
# グループAとBの差は「標準誤差の約3.7倍」に設定
# (通常の95%CIは重なるが、有意差はある絶妙な距離)
n_per_group <- 30
sd_val <- 5
se_expected <- sd_val / sqrt(n_per_group) # 約 0.91
# 平均値の設定
mean_A <- 10
mean_B <- 10 + (3.7 * se_expected) # Aとの差は約3.4
mean_C <- 10 - (1.0 * se_expected) # Aと差がない
cat("--- サンプルデータの設計 ---\n")
cat(sprintf("設定された真の平均値: A=%.2f, B=%.2f, C=%.2f\n", mean_A, mean_B, mean_C))
cat(sprintf("期待される標準誤差(SE): %.2f\n\n", se_expected))
df_sim <- data.frame(
Group = rep(c("A", "B", "C"), each = n_per_group),
Value = c(
rnorm(n_per_group, mean = mean_A, sd = sd_val),
rnorm(n_per_group, mean = mean_B, sd = sd_val),
rnorm(n_per_group, mean = mean_C, sd = sd_val)
)
)
# 2. 統計量の計算
# グループごとの平均、標準偏差、SE、自由度を計算
stats_df <- df_sim %>%
group_by(Group) %>%
summarise(
Mean = mean(Value),
SD = sd(Value),
n = n(),
SE = SD / sqrt(n),
.groups = "drop"
)
# 全体の自由度 (df)
total_df <- sum(stats_df$n) - nrow(stats_df)
k <- nrow(stats_df) # グループ数
cat("--- グループ別統計量 ---\n")
print(stats_df)--- サンプルデータの設計 ---
設定された真の平均値: A=10.00, B=13.38, C=9.09
期待される標準誤差(SE): 0.91
--- グループ別統計量 ---
# A tibble: 3 × 5
Group Mean SD n SE
<chr> <dbl> <dbl> <int> <dbl>
1 A 9.81 5.63 30 1.03
2 B 13.4 5.23 30 0.954
3 C 7.52 5.38 30 0.982 qmvt による SMMクリティカル値の計算
求める分位点(棄却限界値)は 両側95% とします。
# 3. クリティカル・バリューの計算 (qmvtの利用)
# (1) 通常のt分布のクリティカル値 (95%両側)
# Bonferroni補正なしの単純なCI用
qt_crit <- qt(0.975, df = total_df)
# (2) ガブリエル区間用のクリティカル値 (SMM分布)
# SMM分布は、相関行列が単位行列である多変量t分布と等価です。
# tail = "both.tails" で絶対値の最大値を考えます。
corr_mat <- diag(k) # 単位行列 (グループ間は独立とみなす)
qmvt_res <- qmvt(
p = 0.95,
df = total_df,
corr = corr_mat,
tail = "both.tails",
seed = seed
)
qsmm_crit <- qmvt_res$quantile
cat("--- クリティカル値 ---\n")
cat(sprintf("通常のt値 (95%%): %.4f\n", qt_crit))
cat(sprintf("SMM値 (Gabriel用): %.4f\n\n", qsmm_crit))
# 4. 区間幅の計算
# ガブリエル区間の半径 = (SMM値 * SE) / sqrt(2)
# sqrt(2) で割ることで、区間の重なり判定が検定と一致するように調整される
plot_df <- stats_df %>%
mutate(
# 通常の95%信頼区間
CI_Lower = Mean - qt_crit * SE,
CI_Upper = Mean + qt_crit * SE,
# ガブリエル比較区間
Gab_Width = (qsmm_crit * SE) / sqrt(2),
Gab_Lower = Mean - Gab_Width,
Gab_Upper = Mean + Gab_Width
)
cat("--- 算出された区間幅 ---\n")
print(plot_df %>% select(Group, CI_Lower, CI_Upper, Gab_Lower, Gab_Upper))
# 5. 可視化 (エラーバーの重なり比較)
# 見やすくするために、データを縦持ちに変換して描画
plot_data_long <- bind_rows(
plot_df %>% mutate(Type = "通常の95%信頼区間", Lower = CI_Lower, Upper = CI_Upper),
plot_df %>% mutate(Type = "ガブリエル比較区間", Lower = Gab_Lower, Upper = Gab_Upper)
)
p1 <- ggplot(plot_data_long, aes(x = Group, y = Mean, color = Type)) +
# エラーバー
geom_errorbar(aes(ymin = Lower, ymax = Upper),
width = 0.2, size = 1.2, position = position_dodge(width = 0.5)
) +
# 平均値の点
geom_point(size = 4, position = position_dodge(width = 0.5)) +
# AとBの境界線(比較用)
geom_segment(
aes(
x = 0.8, xend = 2.2,
y = plot_df$CI_Upper[plot_df$Group == "A"],
yend = plot_df$CI_Upper[plot_df$Group == "A"]
),
linetype = "dotted", color = "blue", alpha = 0.5
) +
geom_segment(
aes(
x = 0.8, xend = 2.2,
y = plot_df$Gab_Upper[plot_df$Group == "A"],
yend = plot_df$Gab_Upper[plot_df$Group == "A"]
),
linetype = "dotted", color = "red", alpha = 0.5
) +
labs(
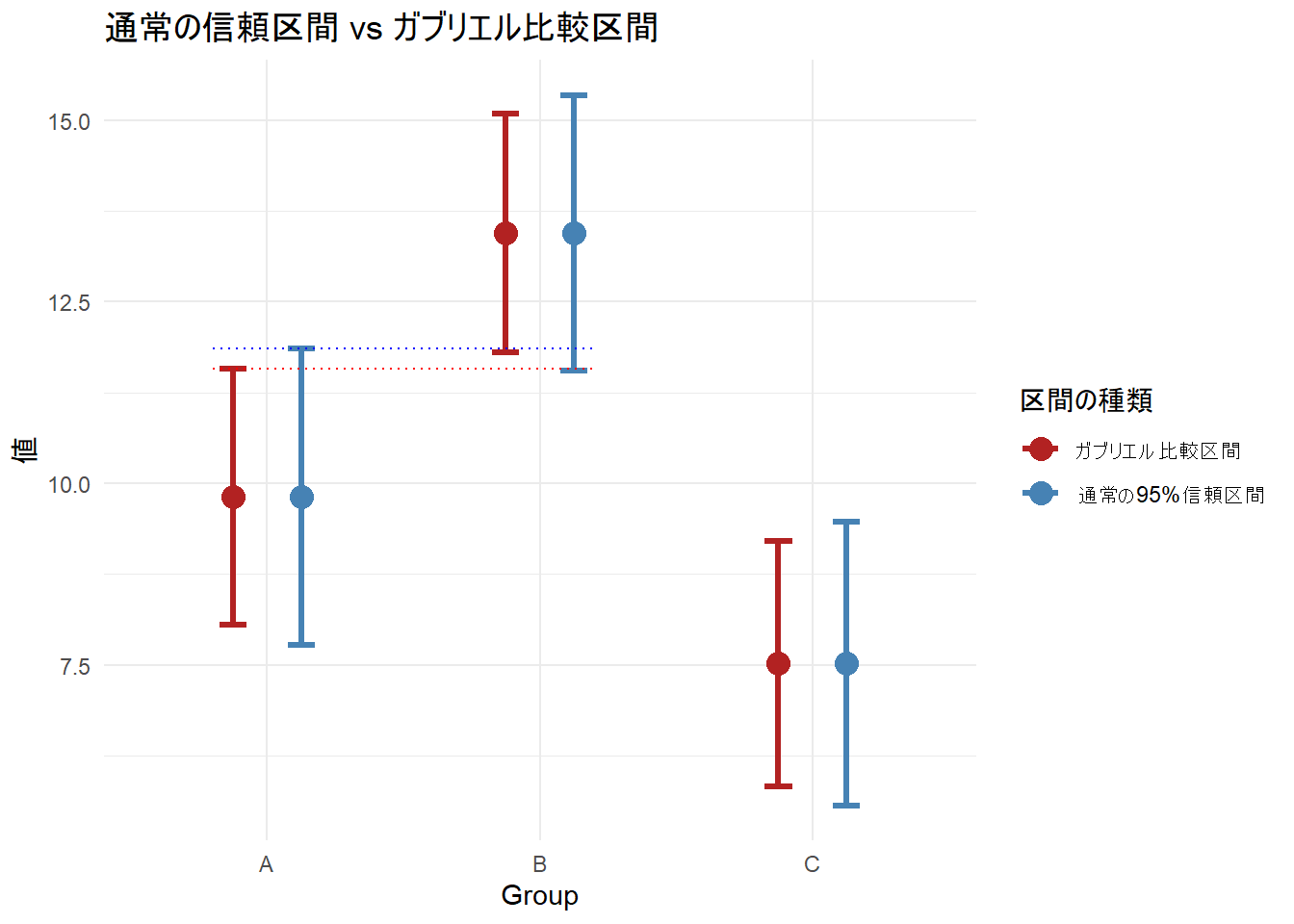
title = "通常の信頼区間 vs ガブリエル比較区間",
y = "値",
color = "区間の種類"
) +
scale_color_manual(values = c(
"通常の95%信頼区間" = "steelblue",
"ガブリエル比較区間" = "firebrick"
)) +
theme_minimal()
print(p1)--- クリティカル値 ---
通常のt値 (95%): 1.9876
SMM値 (Gabriel用): 2.4327
--- 算出された区間幅 ---
# A tibble: 3 × 5
Group CI_Lower CI_Upper Gab_Lower Gab_Upper
<chr> <dbl> <dbl> <dbl> <dbl>
1 A 7.77 11.9 8.05 11.6
2 B 11.6 15.3 11.8 15.1
3 C 5.57 9.47 5.83 9.21Figure 1 の『グループAの上限』と『グループBの下限』を確認しますと、通常の信頼区間(青)では Aの上限 > Bの下限 となっており、バーが重なっていますが、ガブリエル区間(赤)では Aの上限 < Bの下限 となっており、隙間があるため、『バーが重ならない=有意差あり』と視覚的に正しく判定することができます。
\(\sqrt{2}\) で割る理由
「統計的に有意」である条件
2つのグループ A と B の平均値(\(\bar{X}_A, \bar{X}_B\))に有意差があるかどうかを検定する場合、その差の標準誤差(\(SE_{diff}\))は以下のようになります(標準誤差 \(SE\) が同じと仮定)。
\[ SE_{diff} = \sqrt{SE^2 + SE^2} = \sqrt{2 SE^2} = \sqrt{2} \times SE \]
検定統計量 \(q\)(ここではSMM分布のクリティカル値)を使うと、有意差がある条件は以下のようになります。
\[ |\bar{X}_A - \bar{X}_B| > q \times (\sqrt{2} \times SE) \]
つまり、平均値の距離が \(\sqrt{2} \approx 1.414\) 倍以上 離れていれば「有意」です。
「見た目で重ならない」条件
一方、グラフ上でエラーバー(区間の片側の幅を \(w\) とします)を描いたとき、2つの区間が重ならない条件は単純な足し算です。
\[ |\bar{X}_A - \bar{X}_B| > w + w = 2w \]
つまり、平均値の距離が \(2\) 倍以上 離れていれば「重ならない」です。
ズレの調整(\(\sqrt{2}\)で割る理由)
- 統計的な基準: 1.414 (\(=\sqrt{2}\)) 倍離れればOK
- 見た目の基準: 2.0 倍離れないと隙間ができない
つまり、「実際は有意であるのに(1.5倍くらい離れている)、見た目では重なってしまう(2.0倍には届かない)」ことになります。
そこで、「見た目の基準(2倍)」が「統計的な基準(\(\sqrt{2}\)倍)」と等しくなるように、バーの長さ \(w\) を短く調整します。
\[ 2w = \sqrt{2} \times q \times SE \]
この式を変形して \(w\)(ガブリエル区間の幅)を求めます。
\[ w = \frac{\sqrt{2} \times q \times SE}{2} \]
ここで、分母の \(2\) は \(\sqrt{2} \times \sqrt{2}\) ですので、約分できます。
\[ w = \frac{q \times SE}{\sqrt{2}} \]
rgabriel{rgabriel} との比較
ガブリエル比較区間を求めるための関数rgabriel{rgabriel}と結果を比較します。
# パッケージの読み込み
library(rgabriel)
cat("--- mvtnorm::qmvt を用いた手計算 ---\n")
# ガブリエル区間の半径 (Half-Width) の計算
# w = (q * SE) / sqrt(2)
q_smm_manual <- qmvt_res$quantile
stats_df$Manual_Radius <- (q_smm_manual * stats_df$SE) / sqrt(2)
cat(sprintf("SMMクリティカル値 (mvtnorm): %.4f\n", q_smm_manual))
cat("求められた半径:\n")
print(stats_df %>% select(Group, Manual_Radius))
cat("\n--- rgabriel::rgabriel を用いた計算 ---\n")
# rgabriel関数の実行
# 戻り値は各グループの「区間の半径」のベクトルです
pkg_radius <- rgabriel(df_sim$Value, df_sim$Group)
# 結果をデータフレームに結合
stats_df$Pkg_Radius <- pkg_radius
cat("求められた半径:\n")
print(stats_df %>% select(Group, Pkg_Radius))
cat("\n")
cat("\n--- 結果の比較 ---\n")
stats_df$Diff <- stats_df$Manual_Radius - stats_df$Pkg_Radius
print(stats_df %>% select(Group, Manual_Radius, Pkg_Radius, Diff))
# 視覚化による確認
p_comp <- ggplot(stats_df, aes(x = Group)) +
geom_errorbar(aes(ymin = Mean - Manual_Radius, ymax = Mean + Manual_Radius),
width = 0.2, color = "blue", size = 2, alpha = 0.5
) +
geom_errorbar(aes(ymin = Mean - Pkg_Radius, ymax = Mean + Pkg_Radius),
width = 0.2, color = "red", size = 0.5
) +
geom_point(aes(y = Mean), size = 3) +
labs(
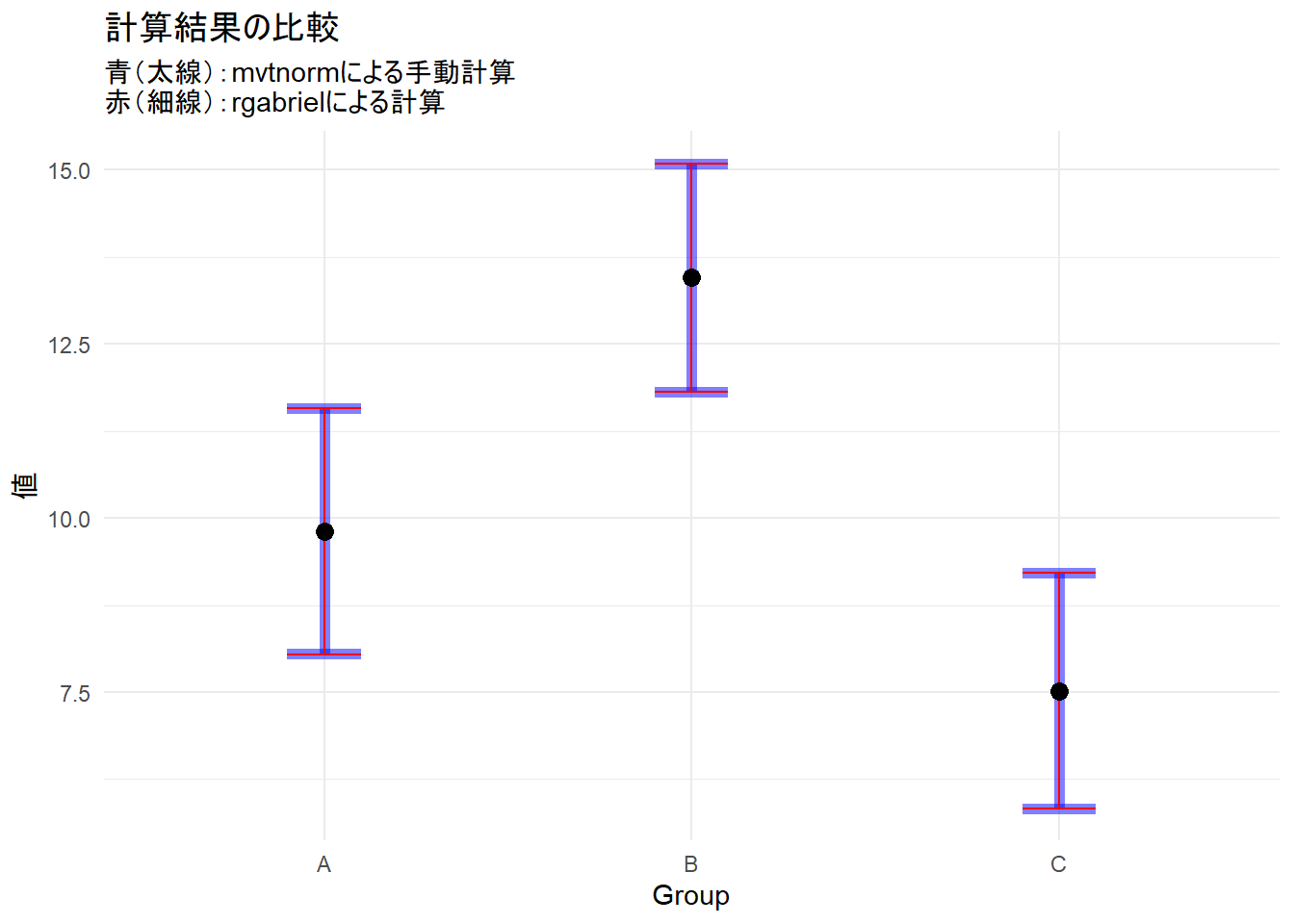
title = "計算結果の比較",
subtitle = "青(太線):mvtnormによる手動計算\n赤(細線):rgabrielによる計算",
y = "値"
) +
theme_minimal()
print(p_comp)--- mvtnorm::qmvt を用いた手計算 ---
SMMクリティカル値 (mvtnorm): 2.4327
求められた半径:
# A tibble: 3 × 2
Group Manual_Radius
<chr> <dbl>
1 A 1.77
2 B 1.64
3 C 1.69
--- rgabriel::rgabriel を用いた計算 ---
求められた半径:
# A tibble: 3 × 2
Group Pkg_Radius
<chr> <dbl[1d]>
1 A 1.77
2 B 1.64
3 C 1.69
--- 結果の比較 ---
# A tibble: 3 × 4
Group Manual_Radius Pkg_Radius Diff
<chr> <dbl> <dbl[1d]> <dbl[1d]>
1 A 1.77 1.77 -0.0000825
2 B 1.64 1.64 -0.0000766
3 C 1.69 1.69 -0.0000788ほぼ、一致しています。
なお、SMM分布のクリティカル値計算アルゴリズムに以下の違いがあります。
-
mvtnorm: 準モンテカルロ法を用いた数値積分。 -
rgabriel: 独自の1次元数値積分(integrate関数)と近似ロジック。
以上です。