Rの関数:cancor {stats}

Rの関数から cancor {stats} を確認します。

関数 `cancor` とは

cancor は、正準相関分析 (Canonical Correlation Analysis, CCA) を実行するための関数です。

正準相関分析とは、2つの変数群（変数のセット $X$ と変数のセット $Y$）が存在する場合に、それぞれの変数群の線形結合（重み付き和）を作成し、その線形結合同士の相関係数（ピアソンの積率相関係数）が最大になるような重み係数を求める多変量解析の手法です。

具体的には、以下の手順で計算が行われます。

変数群 $X$ の線形結合 $U = a_1X_1 + a_2X_2 + \dots$ を作成します。
変数群 $Y$ の線形結合 $V = b_1Y_1 + b_2Y_2 + \dots$ を作成します。
$U$ と $V$ の相関係数が最大となるような係数ベクトル $a$ と $b$ を算出します。この最大の相関係数を「第1正準相関係数」と呼び、$U, V$ を「第1正準変数」と呼びます。
続いて、第1正準変数と無相関であるという制約の下で、次に相関が高くなる組み合わせ（第2正準相関係数）を順次求めていきます。

cancor 関数は、特異値分解（SVD）を用いてこれらの相関係数と係数を計算します。

関数 `cancor` の引数

args(cancor)

function (x, y, xcenter = TRUE, ycenter = TRUE) 
NULL

x
- 第1の変数群を表す数値行列（Matrix）またはデータフレーム。
- 各行が観測値（サンプル）、各列が変数を表します。y と行数（サンプルサイズ）が一致している必要があります。
y
- 第2の変数群を表す数値行列（Matrix）またはデータフレーム。
- x と行数（サンプルサイズ）が一致している必要があります。
xcenter
- x の中心化（Centering）に関する指定です。
- 論理値 (TRUE/FALSE) の場合: TRUE（デフォルト）を指定すると、各列の平均値を引き算して中心化を行います。FALSE の場合、中心化を行わず、ゼロを原点として扱います。
- 数値ベクトルの場合: 指定された数値を各列から引き算します。
- 目的: 相関分析は通常、平均からの偏差に基づいて行われるため、デフォルトで中心化が行われます。
ycenter
- y の中心化に関する指定です。
- xcenter と同様に機能します。TRUE（デフォルト）の場合、y の各列から平均値を引きます。

シミュレーションコード

以下に、cancor の挙動を確認するためのサンプルデータを用いたシミュレーションコードを示します。

このシミュレーションでは、「潜在的な共通因子」 を想定してデータを生成します。

2つの変数群 $X$ と $Y$ は、背後にある共通の要因（潜在因子）によって部分的に相関しています。
この構造を cancor が見抜き、共通因子に沿った軸（正準変数）を抽出できるかを確認します。

シミュレーションデータの生成

データ概要:

観測数: 500
変数群 X: 3変数 (潜在因子1, 2の影響を受ける)
変数群 Y: 3変数 (潜在因子1, 2の影響を受ける。Y_Noiseは無関係)
期待される結果:
- 第1正準相関: 潜在因子1を捉え、高い相関を示すはず
- 第2正準相関: 潜在因子2を捉え、ある程度の相関を示すはず
- 第3正準相関: ノイズ同士の関係なので、相関は低いはず

# パッケージの読み込み
library(ggplot2)
library(tidyr)
library(gridExtra)

# 乱数シードの固定
seed <- 20260120
set.seed(seed)

# 設定: サンプルサイズ 500
n <- 500

# 1. 潜在的な共通因子 (Latent Factors) の生成
# 変数群XとYの両方に影響を与える「真の原因」
# Factor_1: 強い共通要因
# Factor_2: 中程度の共通要因
latent_1 <- rnorm(n, mean = 0, sd = 1)
latent_2 <- rnorm(n, mean = 0, sd = 1)

# 2. 変数群 X の生成 (3変数)
# X1: Factor_1 を強く反映
# X2: Factor_2 を反映
# X3: 両方の要素 + 独自ノイズ
X <- matrix(0, nrow = n, ncol = 3)
colnames(X) <- c("X_Main", "X_Sub", "X_Mix")
X[, 1] <- 1.5 * latent_1 + rnorm(n, 0, 0.5)
X[, 2] <- 1.0 * latent_2 + rnorm(n, 0, 0.5)
X[, 3] <- 0.5 * latent_1 + 0.5 * latent_2 + rnorm(n, 0, 1.0)

# 3. 変数群 Y の生成 (3変数)
# Y1: Factor_1 を強く反映
# Y2: Factor_2 とは逆相関
# Y3: ほぼノイズ（相関に関係ない変数）
Y <- matrix(0, nrow = n, ncol = 3)
colnames(Y) <- c("Y_Main", "Y_Inverse", "Y_Noise")
Y[, 1] <- 1.2 * latent_1 + rnorm(n, 0, 0.5)
Y[, 2] <- -1.0 * latent_2 + rnorm(n, 0, 0.5)
Y[, 3] <- rnorm(n, 0, 1.0) # 共通因子と無関係

cat("--- 生成したサンプルデータの一部を確認 ---\n")
head(X)
head(Y)

--- 生成したサンプルデータの一部を確認 ---
         X_Main       X_Sub      X_Mix
[1,]  0.5732728 0.006331994 -0.3958316
[2,] -0.3227754 0.809846715  0.3249550
[3,] -1.1379111 3.546305556  1.5645093
[4,]  2.8554113 0.260545685  0.9542788
[5,] -1.2255349 0.603725413 -1.1732257
[6,]  0.6059975 0.151445558  3.0775268
         Y_Main   Y_Inverse    Y_Noise
[1,] -0.1402206  0.63103409  1.2060194
[2,]  0.3370663 -0.04760007  1.2322705
[3,] -1.3063783 -2.30873162 -0.8070207
[4,]  2.3456446  0.26752998  1.2141281
[5,] -1.9671118 -0.49902408  0.4448520
[6,]  0.5597343 -1.35775876 -2.7346056

正準相関分析 (cancor) の実行

# cancor関数の実行
# xcenter, ycenterはデフォルト(TRUE)で、自動的に中心化されます
cca_res <- cancor(X, Y)

# 結果の要素を確認
# cca_res$cor: 正準相関係数
# cca_res$xcoef: X側の正準係数 (重み)
# cca_res$ycoef: Y側の正準係数 (重み)

cat("--- 正準相関係数 (Canonical Correlations) ---\n")
print(cca_res)

--- 正準相関係数 (Canonical Correlations) ---
$cor
[1] 0.88876918 0.81756779 0.00653527

$xcoef
               [,1]        [,2]        [,3]
X_Main  0.028027014 0.003611073  0.01475633
X_Sub  -0.006696897 0.035222077  0.02152600
X_Mix   0.001718242 0.004828756 -0.04400035

$ycoef
                   [,1]         [,2]          [,3]
Y_Main     0.0349616415  0.005850044 -0.0005333954
Y_Inverse  0.0065967612 -0.036991164  0.0019908313
Y_Noise   -0.0004967812  0.001702025  0.0436393690

$xcenter
      X_Main        X_Sub        X_Mix 
-0.004302858 -0.025224575 -0.036417000 

$ycenter
     Y_Main   Y_Inverse     Y_Noise 
-0.09648480  0.05979862 -0.01039909

`$cor`（正準相関係数）

ここには、確認された「つながりの強さ」が順に表示されています。

第1成分 (0.8888):
- 強い相関です。これが 「潜在因子1 (Factor_1)」 によって生じた関係です。
第2成分 (0.8176):
- こちらも強い相関です。これが 「潜在因子2 (Factor_2)」 によって生じた関係です。
第3成分 (0.0065):
- ほぼゼロです。残った成分（ノイズ）同士には関係性がないことを正しく示しています。

よって、データには「2つの強いつながり」があることが確認されました。

`$xcoef` と `$ycoef`（正準係数）

この係数は、「どの変数を重視して合成変数（正準変数）を作ったか」を表す重みです。各列が第1、第2、第3成分に対応します。

[,1]列：第1正準変数

X側 ($xcoef):
- X_Main の係数 (0.028) が、他（-0.006, 0.001）に比べて正の方向に大きいです。
Y側 ($ycoef):
- Y_Main の係数 (0.035) が、他（0.006, -0.000）に比べて大きいです。
解釈:
- お互いに 「Main（Factor_1の影響大）」 の変数を重視してペアを作っています。つまり、第1正準変数は 「潜在因子1」 を抽出した軸です。

[,2]列：第2正準変数

X側 ($xcoef):
- X_Sub の係数 (0.035) が最も大きいです。これは Factor_2 を反映する変数です。
Y側 ($ycoef):
- Y_Inverse の係数 (-0.037) の絶対値が最も大きいです。
解釈:
- お互いに 「Factor_2に関連する変数」 を重視しています。
- 符号に注目しますと、X側はプラス、Y側はマイナスです。
- これは、データ生成時に Y_Inverse を「逆相関（-1.0 * latent_2）」で作った設定を捉えている結果です（Xが増えるとYが減る関係）。

[,3]列：第3正準変数

Y側:
- Y_Noise (0.043) が最大です。
解釈:
- 共通因子とは無関係なノイズ変数がここに押し出されています。相関係数（$cor）がほぼゼロですので、この軸に統計的な意味はありません。

`$xcenter` と `$ycenter`

これらは分析の前処理として計算された「各変数の平均値」です。cancor 関数は、これらの値をデータから引いて中心化（平均0化）を行ってから計算したことを示しています。

まとめ

この結果は、cancor が単に相関が高いものを見つけるだけでなく、「データの中に隠れている複数の異なる関係性（因子1のつながり、因子2のつながり）」を分離して抽出できた ことを示しています。

正準変数の計算と可視化

# 正準変数のスコアを計算
# 注意: cancorは中心化を行うため、手動計算時も中心化データの積をとるのが厳密ですが、
# 相関を見る目的では、係数をそのまま掛けても形状は同じです。
# ここでは厳密に中心化してから適用します。
X_centered <- scale(X, center = TRUE, scale = FALSE)
Y_centered <- scale(Y, center = TRUE, scale = FALSE)

# 第1正準変数 (U1, V1)
U1 <- X_centered %*% cca_res$xcoef[, 1]
V1 <- Y_centered %*% cca_res$ycoef[, 1]

# 第2正準変数 (U2, V2)
U2 <- X_centered %*% cca_res$xcoef[, 2]
V2 <- Y_centered %*% cca_res$ycoef[, 2]

# データフレームにまとめる
df_plot <- data.frame(
  U1 = U1, V1 = V1,
  U2 = U2, V2 = V2
)

# プロット作成
# 第1正準変数の散布図
p1 <- ggplot(df_plot, aes(x = U1, y = V1)) +
  geom_point(alpha = 0.5, color = "blue") +
  geom_smooth(method = "lm", color = "red", se = FALSE) +
  labs(
    title = "図1: 第1正準変数の関係 (最も強い相関)",
    subtitle = paste0("相関係数: ", round(cor(U1, V1), 4)),
    x = "X側の第1正準変数 (U1)",
    y = "Y側の第1正準変数 (V1)"
  ) +
  theme_minimal()

# 第2正準変数の散布図
p2 <- ggplot(df_plot, aes(x = U2, y = V2)) +
  geom_point(alpha = 0.5, color = "darkgreen") +
  geom_smooth(method = "lm", color = "red", se = FALSE) +
  labs(
    title = "図2: 第2正準変数の関係 (次に強い相関)",
    subtitle = paste0("相関係数: ", round(cor(U2, V2), 4)),
    x = "X側の第2正準変数 (U2)",
    y = "Y側の第2正準変数 (V2)"
  ) +
  theme_minimal()

# 並べて表示
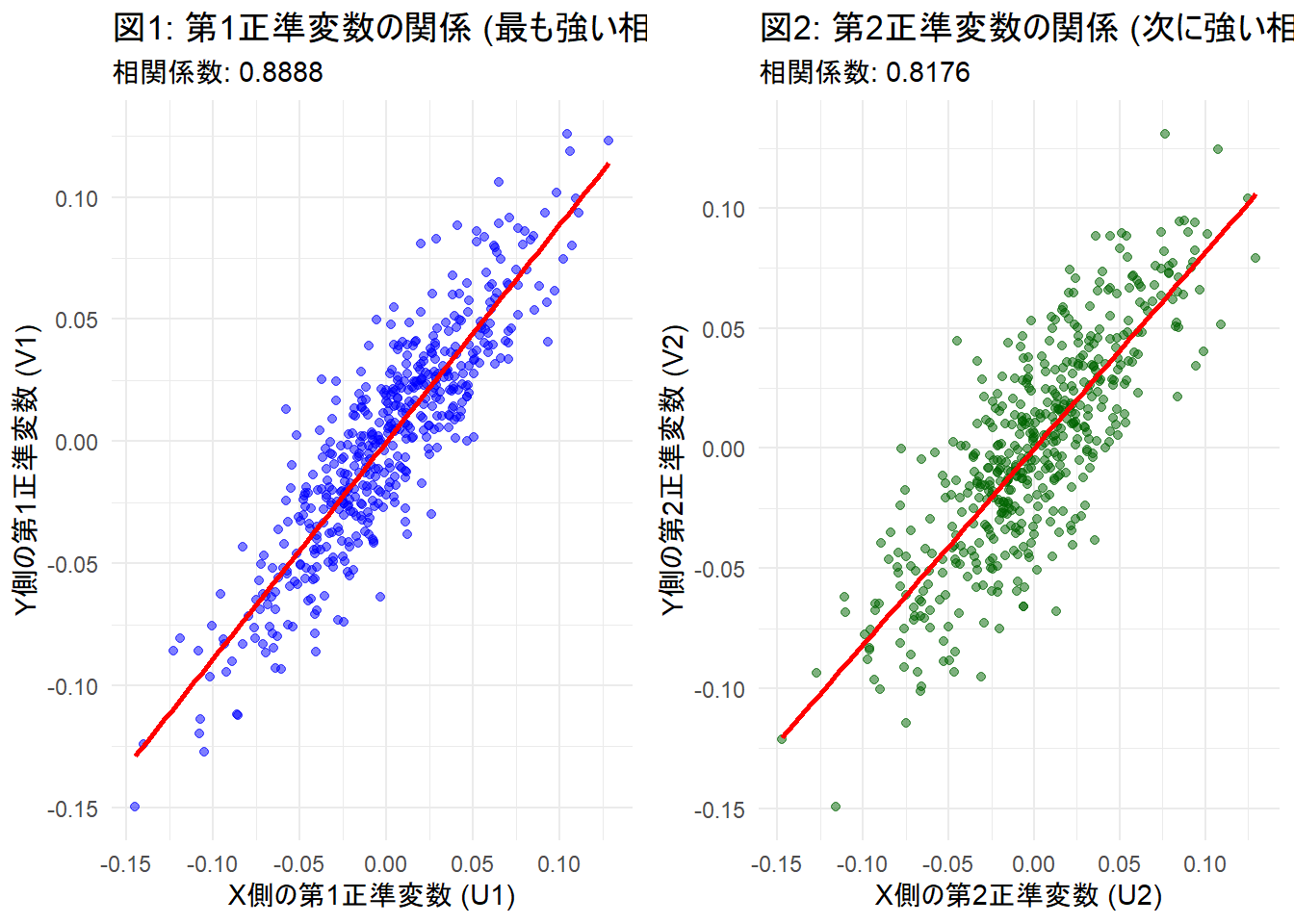
grid.arrange(p1, p2, ncol = 2)

図1（左）：第1正準変数の関係

変数群Xから作った合成変数 $U_1$ と、変数群Yから作った合成変数 $V_1$ の散布図です。
青い点が赤い回帰直線の周りに密集しており、強い直線関係があることが分かります。これは、シミュレーションで設定した最も強力な共通要因である「潜在因子1（Factor_1）」を、CCAが第1成分として的確に捉えたことを意味します。X群とY群は、この軸において最も強く連動しています。

図2（右）：第2正準変数の関係

第1成分とは無相関になるように作られた、次の合成変数ペア $U_2, V_2$ の散布図です。
第1成分（図1）の影響を完全に取り除いた後でも、強い相関が残っていることが可視化されています。これは、データに潜ませたもう一つの共通要因である「潜在因子2（Factor_2）」を、CCAが第2成分として分離して抽出できたことを示しています。

結論

この2つの図は、CCAのアルゴリズムが、「ごちゃ混ぜになった変数群の中から、『1つ目の強いつながり（図1）』と、それとは全く質の異なる『2つ目の強いつながり（図2）』を切り分け」ていることを示しています。

以上です。

関数 cancor とは

関数 cancor の引数