Rの関数から pwilcox {stats} を確認します。
本ポストはこちらの続きです。

関数 pwilcox とは
pwilcox は、ウィルコクソンの順位和検定(Wilcoxon Rank Sum Test) における検定統計量 \(W\)(マン・ホイットニーの \(U\) 統計量と等価)の 累積分布関数(Cumulative Distribution Function: CDF) を計算する関数です。
ウィルコクソンの順位和検定は、2つの独立した群の分布の位置に差があるかを検定するノンパラメトリック手法です。
帰無仮説(2つの群の分布は等しい)が正しい場合、統計量 \(W\) は特定の離散分布に従います。
pwilcox は、統計量 \(W\) がある値 \(q\) 以下になる確率 \(P(W \le q)\) を計算します。
これは、検定における P値(P-value) を算出するための基礎となります。
注意点として、ここでの統計量 \(W\) は「順位の合計」そのものではなく、「順位の合計から最小値を引いたもの(0から始まる値)」として定義されます。
関数 pwilcox 引数
-
q- 確率を計算したい統計量 \(W\) の値(分位点)。
- ベクトル形式で指定可能です。\(W\) のとりうる値の範囲は \(0\) から \(m \times n\) です。
-
m- 第1の標本のサンプルサイズ(整数)。
- 正の整数である必要があります。
-
n- 第2の標本のサンプルサイズ(整数)。
- 正の整数である必要があります。
-
lower.tail- 累積確率を計算する方向を指定する論理値。
- デフォルト:
TRUE。 -
TRUEの場合、\(P(W \le q)\) (左側の裾の確率)を計算します。 -
FALSEの場合、\(P(W > q)\) (右側の裾の確率)を計算します。これは \(1 - P(W \le q)\) と等価です。
-
log.p- 結果を対数確率(log scale)で返すかどうかの論理値。
- デフォルト:
FALSE。 - 非常に小さな確率を扱う際、アンダーフロー(数値計算上の誤差で0になってしまうこと)を防ぐために使用されます。
シミュレーションコード
以下に、pwilcox の機能を確認するためのシミュレーションコードを示します。
このシミュレーションでは、以下の手順を行います。
- 理論的な分布の確認:
-
pwilcoxを用いて、特定のサンプルサイズにおける統計量 \(W\) の累積分布を計算します。
-
- モンテカルロ・シミュレーション:
- 実際にランダムなデータを多数生成してウィルコクソン検定を行い、その統計量 \(W\) の分布が
pwilcoxの理論値と一致することを検証します。
- 実際にランダムなデータを多数生成してウィルコクソン検定を行い、その統計量 \(W\) の分布が
パラメータ設定
# パッケージの読み込み
library(ggplot2)
library(dplyr)
# 1. パラメータ設定
# 小規模なサンプルサイズを設定(計算過程を理解しやすくするため)
m_size <- 5 # グループAのサンプル数
n_size <- 4 # グループBのサンプル数
# 統計量 W のとりうる最大値は m * n
w_max <- m_size * n_size
cat("--- 設定パラメータ ---\n")
cat(sprintf("グループAのサイズ (m): %d\n", m_size))
cat(sprintf("グループBのサイズ (n): %d\n", n_size))
cat(sprintf("統計量 W の範囲: 0 ~ %d\n\n", w_max))--- 設定パラメータ ---
グループAのサイズ (m): 5
グループBのサイズ (n): 4
統計量 W の範囲: 0 ~ 20理論的な累積分布の計算 (pwilcoxを使用)
# 2. 理論的な累積分布の計算 (pwilcoxを使用)
# 0 から w_max までの全ての q について確率を計算
q_vals <- 0:w_max
prob_vals <- pwilcox(q = q_vals, m = m_size, n = n_size)
# データフレーム化
df_theoretical <- data.frame(
q = q_vals,
Probability = prob_vals,
Type = "理論値 (pwilcox)"
)
cat("--- pwilcoxによる計算例 ---\n")
cat(sprintf("W <= 5 となる確率: %.4f\n", pwilcox(5, m_size, n_size)))
cat(sprintf("W <= 10 となる確率: %.4f (分布の中央)\n", pwilcox(10, m_size, n_size)))
cat(sprintf("W <= 15 となる確率: %.4f\n\n", pwilcox(15, m_size, n_size)))--- pwilcoxによる計算例 ---
W <= 5 となる確率: 0.1429
W <= 10 となる確率: 0.5476 (分布の中央)
W <= 15 となる確率: 0.9048モンテカルロ・シミュレーションによる検証
# 3. モンテカルロ・シミュレーションによる検証
# 帰無仮説(2つの分布は同じ)が正しい状況を作り出し、
# ランダムにデータを生成して W 統計量を計算することを繰り返す
# 乱数シードの固定
seed <- 20260127
set.seed(seed)
n_sim <- 10000 # シミュレーション回数
w_simulated <- numeric(n_sim)
for (i in 1:n_sim) {
# 同一の分布(一様分布)からランダムにサンプリング
sample_A <- runif(m_size)
sample_B <- runif(n_size)
# wilcox.test を実行して統計量 W を取得
# (exact=TRUE で正確な値を計算)
res <- wilcox.test(sample_A, sample_B, exact = TRUE)
w_simulated[i] <- res$statistic
}
# シミュレーション結果の累積分布を計算
df_empirical <- data.frame(W = w_simulated) %>%
group_by(W) %>%
summarise(Count = n(), .groups = "drop") %>%
mutate(
Probability = cumsum(Count) / sum(Count),
q = W,
Type = "シミュレーション値"
) %>%
select(q, Probability, Type)
# 理論値とシミュレーション値を結合(欠けているW値を補完するためにマージ)
df_all <- merge(df_theoretical, df_empirical, by = c("q", "Type", "Probability"), all = TRUE)
# 可視化
# 理論的なカーブ(線)とシミュレーション結果(点)を重ねて表示
p1 <- ggplot() +
# 理論値 (pwilcox) のライン
geom_step(
data = df_theoretical, aes(x = q, y = Probability, color = "理論値 (pwilcox)"),
linewidth = 1.2
) +
# シミュレーション値のポイント
geom_point(
data = df_empirical, aes(x = q, y = Probability, color = "シミュレーション値"),
size = 3, alpha = 0.6
) +
scale_color_manual(name = NULL, values = c("理論値 (pwilcox)" = "blue", "シミュレーション値" = "orange")) +
labs(
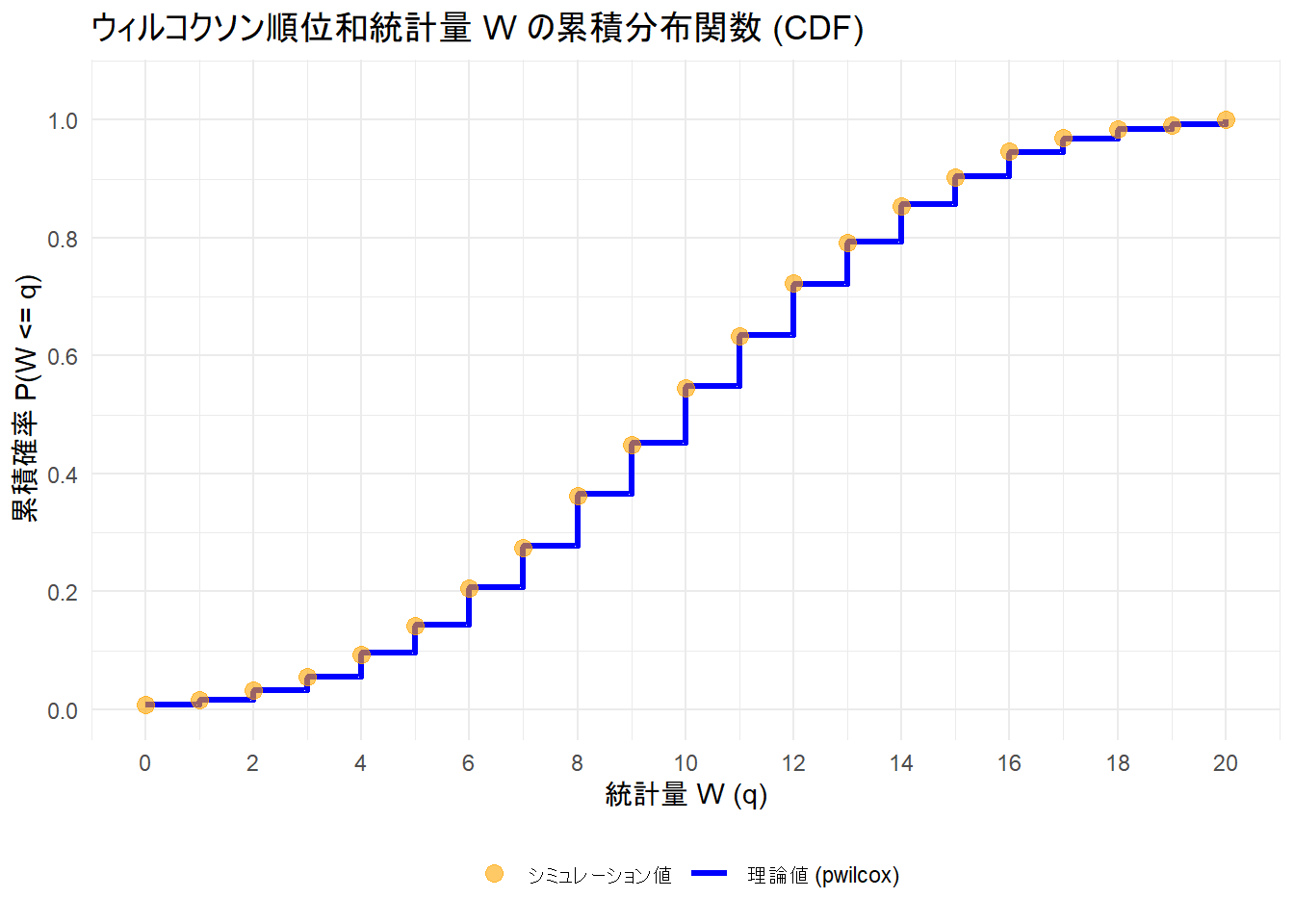
title = "ウィルコクソン順位和統計量 W の累積分布関数 (CDF)",
x = "統計量 W (q)",
y = "累積確率 P(W <= q)"
) +
scale_x_continuous(breaks = seq(0, w_max, 2)) +
scale_y_continuous(breaks = seq(0, 1, 0.2), limits = c(0, 1.05)) +
theme_minimal() +
theme(legend.position = "bottom")
print(p1)Figure 1 の青い階段状の線が pwilcox 関数によって計算された理論的な累積確率分布、オレンジ色の点は、実際にランダムなデータを10,000回生成して得られた結果の累積割合です。
両者が重なっていることが確認できます。
Wilcoxon分布のスクラッチ実装
動的計画法(Dynamic Programming)を用いて、ウィルコクソン順位和統計量 \(W\) の正確な分布(組み合わせの数)を計算します。
ウィルコクソン統計量(マン・ホイットニーの \(U\))の確率分布は、以下の漸化式を用いて計算できます。 \[ N(k, m, n) = N(k - n, m - 1, n) + N(k, m, n - 1) \] ここで \(N(k, m, n)\) は、サンプルサイズ \(m, n\) の時に統計量が \(k\) となる組み合わせの数です。このロジックを2重ループで実装します。
スクラッチ実装コード
# stats::pwilcox のスクラッチ実装
scratch_pwilcox <- function(q, m, n, lower.tail = TRUE, log.p = FALSE) {
# 1. 引数のバリデーション
if (length(m) != 1 || length(n) != 1) stop("m と n は単一の整数でなければなりません")
m <- as.integer(m)
n <- as.integer(n)
# エッジケース: サンプルサイズが0の場合
if (m == 0 || n == 0) {
# 統計量は常に0になるため、q >= 0 なら確率は1
p <- ifelse(q >= 0, 1, 0)
if (!lower.tail) p <- 1 - p
if (log.p) {
return(log(p))
} else {
return(p)
}
}
# 2. 動的計画法 (DP) による分布の計算
# 目的: サイズ(m, n)の時に、統計量Wがkになる組み合わせの数を計算する
# 漸化式: count(k, m, n) = count(k - n, m - 1, n) + count(k, m, n - 1)
# 意味: 「最大のランクを持つ要素」がグループmに属するか、グループnに属するかで場合分け
# 初期化: i=0 (m=0) の状態。W=0 となる組み合わせが1通りだけある。
# current_dists[[j]] には、サイズ(0, j-1) における分布のベクトルを格納
# リストのインデックスはRの仕様上 1 始まりのため、nに対応するデータは index=n+1 に格納
current_dists <- rep(list(c(1)), n + 1)
# i (グループmのサイズ) を 1 から m まで増やしていく
for (i in 1:m) {
next_dists <- list()
# j=0 (グループnのサイズが0) の場合、W=0 の1通りのみ
next_dists[[1]] <- c(1)
# j (グループnのサイズ) を 1 から n まで増やしていく
for (j in 1:n) {
# 漸化式の適用
# 1. count(k - j, i - 1, j) に対応
# 直前のステップ (i-1, j) の分布を取得し、スコアを j だけシフト(加算)する
# (Rのリストインデックスは j+1 を参照)
dist_prev_i <- current_dists[[j + 1]]
shifted_dist <- c(rep(0, j), dist_prev_i) # 先頭に0をj個追加してシフト
# 2. count(k, i, j - 1) に対応
# 同じiのステップでの (i, j-1) の分布を取得
dist_prev_j <- next_dists[[j]] # こちらは既に計算済み
# 3. 2つの分布(ベクトル)を足し合わせる
# ベクトルの長さが異なるため、短い方の末尾を0で埋めて長さを合わせる
len_diff <- length(shifted_dist) - length(dist_prev_j)
if (len_diff > 0) {
dist_prev_j <- c(dist_prev_j, rep(0, len_diff))
} else if (len_diff < 0) {
shifted_dist <- c(shifted_dist, rep(0, -len_diff))
}
# 加算して新しい分布とする
next_dists[[j + 1]] <- shifted_dist + dist_prev_j
}
# 次のイテレーションのために更新
current_dists <- next_dists
}
# 最終的な頻度分布 (サイズ m, n)
freqs <- current_dists[[n + 1]]
# 3. 累積分布関数 (CDF) の計算
# 総組み合わせ数 choose(m + n, m)
total_comb <- sum(freqs)
# 確率質量分布 (PMF) -> 累積分布 (CDF)
probs <- cumsum(freqs) / total_comb
# 4. 入力 q に対応する確率の取得
# q はベクトル対応する必要がある
# 統計量は離散値なので、floor(q) 以下の累積確率を参照する
q_idx <- floor(q)
res_p <- numeric(length(q))
max_w <- length(probs) - 1 # 最大スコア m*n
for (k in seq_along(q)) {
val <- q_idx[k]
if (val < 0) {
res_p[k] <- 0
} else if (val >= max_w) {
res_p[k] <- 1
} else {
# freqs[1] が W=0 に対応するため、インデックスは val + 1
res_p[k] <- probs[val + 1]
}
}
# 5. オプション処理 (lower.tail, log.p)
if (!lower.tail) res_p <- 1 - res_p
if (log.p) res_p <- log(res_p)
return(res_p)
}stats::pwilcox との比較
# テストパラメータ
m <- 5
n <- 4
q_vals <- c(-1, 0, 5, 10, 15, 20, 25) # 境界値を含むテスト
# stats::pwilcox の結果
res_stats <- pwilcox(q_vals, m, n)
# 自作関数の結果
res_my <- scratch_pwilcox(q_vals, m, n)
# 結果の表示
df_compare <- data.frame(
q = q_vals,
stats_pkg = res_stats,
my_func = res_my,
Is_Equal = abs(res_stats - res_my) < 1e-10 # 誤差許容
)
print(df_compare)
cat("\n全ての値が一致しているか確認: ", all(df_compare$Is_Equal), "\n") q stats_pkg my_func Is_Equal
1 -1 0.000000000 0.000000000 TRUE
2 0 0.007936508 0.007936508 TRUE
3 5 0.142857143 0.142857143 TRUE
4 10 0.547619048 0.547619048 TRUE
5 15 0.904761905 0.904761905 TRUE
6 20 1.000000000 1.000000000 TRUE
7 25 1.000000000 1.000000000 TRUE
全ての値が一致しているか確認: TRUE 以上です。