Rの関数:SVAR {vars}

Rの関数から SVAR {vars} を確認します。

本ポストはこちらの続きです。

Rの関数から VAR {vars} 引数 exogen の利用を確認します。本ポストはこちらの続きです。シミュレーションの設計データの構造:内生変数 (y_1, y_2): 互いに影響し合う2つの変数（VAR構造）。外生変数 (x): シ...

関数 `SVAR` とは

SVAR は、構造ベクトル自己回帰（Structural Vector Autoregression）モデルを推定するための関数です。

通常のVARモデル（誘導形VAR）は、変数間の因果関係を過去のラグから予測しますが、「同時点の因果関係」を識別することができません。

例えば、「広告費を増やしたその月に、すぐに売上が増えた」のか、「売上が増えたから、その月のうちに広告費を増やした」のかを区別できません。

SVARモデルは、ドメイン知識等に基づいて変数間の同時点の関係に制約（構造）を与えることで、この識別問題を解決し、「構造的なショック（Structural Shock）」の影響を分析可能にします。

基本式は以下の通りです。 \[ A \mathbf{u}_t = B \mathbf{\epsilon}_t \] ここで、\(\mathbf{u}_t\) はVARの残差ベクトル、\(\mathbf{\epsilon}_t\) は構造的ショック（直交化されたショック）、\(A\) と \(B\) は同時点の関係を表す行列です。

関数 `SVAR` の引数

library(vars)
args(SVAR)

function (x, estmethod = c("scoring", "direct"), Amat = NULL, 
    Bmat = NULL, start = NULL, max.iter = 100, conv.crit = 1e-07, 
    maxls = 1, lrtest = TRUE, ...) 
NULL

x
- VAR() 関数によって推定された varest クラスのオブジェクトです。
- SVARの基礎となる誘導形VARモデルの結果を渡す必要があります。
estmethod
- パラメータの推定方法を指定します。
- 選択肢:
  - "scoring": スコアリングアルゴリズム（デフォルト）。反復計算により尤度を最大化します。
  - "direct": 直接的な最適化（optim 関数を使用）。
Amat
- 左辺の構造行列 \(A\) の制約を指定する行列です。
- 設定方法:
  - 推定したい箇所には NA を指定します。
  - 固定したい箇所（制約）には数値（通常は0や1）を指定します。
  - 例えば、変数1が変数2に同時点の影響を与えないと仮定する場合、\(A\)行列の対応する要素を0に固定します。
Bmat
- 右辺の構造行列 \(B\) の制約を指定する行列です。
- 設定方法: Amat と同様に、推定対象を NA、固定値を数値で指定します。
- モデルタイプ: Amat のみを指定すると Aモデル、Bmat のみを指定すると Bモデル、両方を指定すると ABモデルとなります。
start
- 推定アルゴリズムの初期値を指定するベクトルです。
- デフォルト: NULL（自動的に0.1などが設定されます）。収束しない場合に手動で設定することがあります。
max.iter
- 推定アルゴリズムの最大反復回数です。
- デフォルト: 100。
conv.crit
- 収束判定基準（収束許容誤差）です。
- デフォルト: 1e-07。
maxls
- 直線探索（Line Search）の最大ステップサイズです（スコアリング法のみ）。
lrtest
- 過剰識別制約（Over-identification restrictions）の尤度比検定を行うかどうかの論理値です。
- デフォルト: TRUE。モデルが識別可能（Just-identified）な場合は警告が出ます。

シミュレーションコード

以下に、SVAR 関数の機能を確認するためのサンプルデータを用いたシミュレーションコードを示します。

このシミュレーションでは、3つの変数（変数1, 変数2, 変数3）の間に明確な「同時点の因果関係」を設定します。

構造:

変数1（根源的なショック）は、他の変数に一方的に影響を与える（外生的）。
変数2は、変数1の影響を受けるが、変数3には影響を与えない。
変数3は、変数1と変数2の両方の影響を受ける（最も内生的）。

この構造（再帰的構造、Recursive Structure）を持つデータを生成し、SVAR 関数に制約行列を与えることで、真の同時係数を復元できるか検証します。

なお、有意水準は5%とします。

SVAR用シミュレーションデータの生成

データ概要:

変数の数: 3 (Var1, Var2, Var3)
真の同時点構造 (B行列):
- Var1 は e1 のみから影響を受ける
- Var2 は e1(係数0.5) と e2 から影響を受ける
- Var3 は e1(係数-0.3), e2(係数0.8), e3 から影響を受ける

# パッケージの読み込み
library(ggplot2)
library(tidyr)

# 乱数シードの固定
seed <- 20260104
set.seed(seed)

# 設定: 3変量SVARモデル
n_obs <- 500
K <- 3 # 変数の数

# 1. 構造的ショック (Structural Shocks) の生成
# 互いに独立な標準正規乱数
# epsilon_t ~ N(0, I)
epsilon <- matrix(rnorm(n_obs * K), ncol = K)
colnames(epsilon) <- c("e1", "e2", "e3")

# 2. 同時点の関係行列 (B行列: A u_t = B e_t における B)
# ここでは A = I (単位行列) とし、u_t = B e_t の形（Bモデル）で生成します。
# 構造:
# u1 = 1.0*e1
# u2 = 0.5*e1 + 1.0*e2
# u3 = -0.3*e1 + 0.8*e2 + 1.0*e3
# (下三角行列の構造を持たせる)
B_true <- matrix(c(
  1.0, 0.0, 0.0,
  0.5, 1.0, 0.0,
  -0.3, 0.8, 1.0
), nrow = 3, byrow = TRUE)

# 誘導形残差 (Reduced form residuals) u_t の生成
u_t <- t(B_true %*% t(epsilon))

# 3. VARプロセスの生成 (ダイナミクス)
# y_t = A1 * y_{t-1} + u_t
# 安定的な係数行列を設定
A1_true <- matrix(c(
  0.4, 0.0, 0.0,
  0.1, 0.3, 0.0,
  0.0, 0.1, 0.2
), nrow = 3, byrow = TRUE)

data_sim <- matrix(0, nrow = n_obs, ncol = K)
colnames(data_sim) <- c("Var1", "Var2", "Var3")

for (t in 2:n_obs) {
  y_prev <- data_sim[t - 1, ]
  # VARプロセス + 同時点相関を含む残差
  data_sim[t, ] <- A1_true %*% y_prev + u_t[t, ]
}

df_sim <- as.data.frame(data_sim)

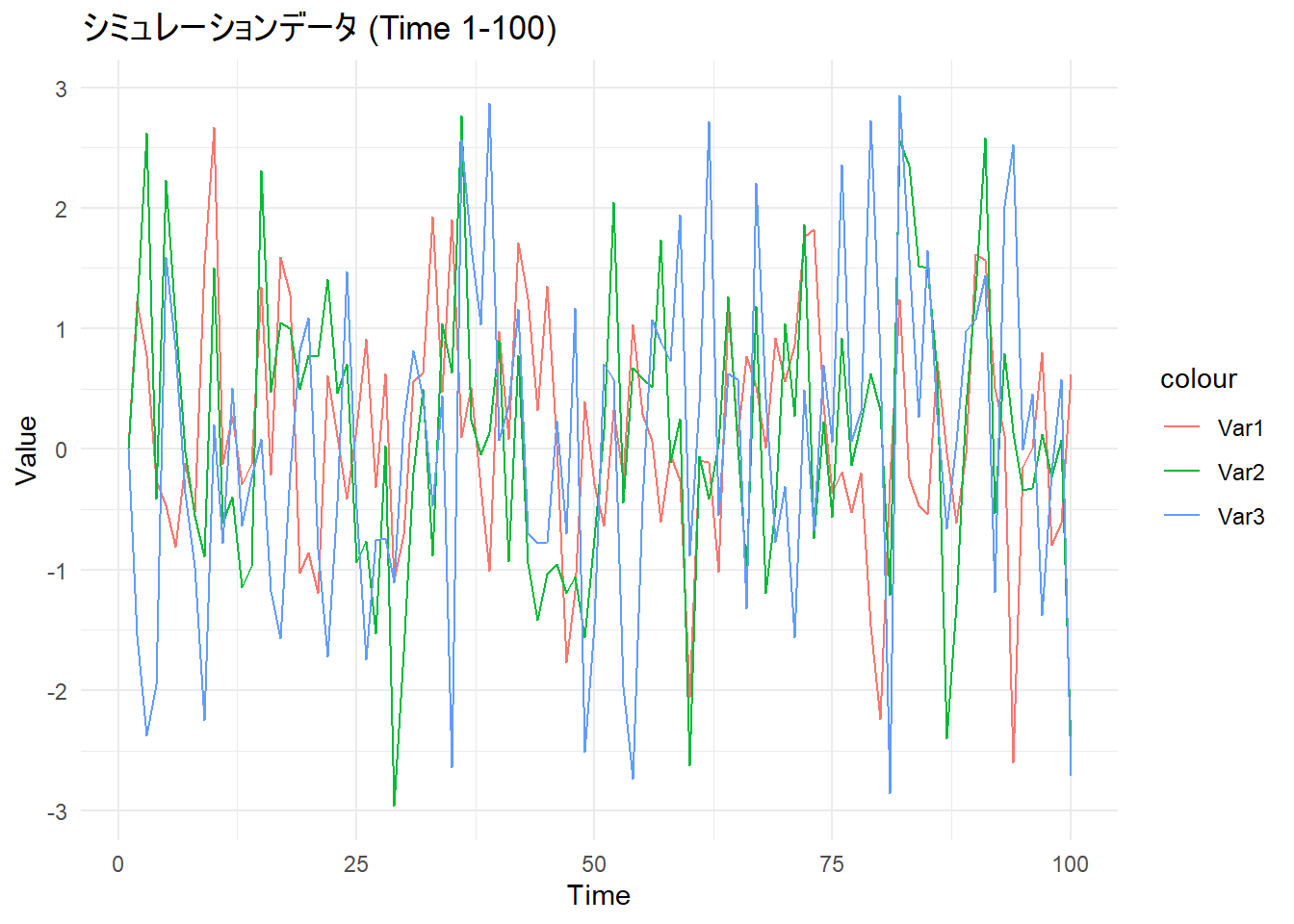
# データの可視化（最初の100時点）
p1 <- ggplot(data = data.frame(Time = 1:100, df_sim[1:100, ]), aes(x = Time)) +
  geom_line(aes(y = Var1, color = "Var1")) +
  geom_line(aes(y = Var2, color = "Var2")) +
  geom_line(aes(y = Var3, color = "Var3")) +
  labs(title = "シミュレーションデータ (Time 1-100)", y = "Value") +
  theme_minimal()

print(p1)

手順1: 誘導形VARモデルの推定

# まず通常のVARモデルを推定します
var_est <- VAR(df_sim, p = 1, type = "none")

print(summary(var_est))


VAR Estimation Results:
========================= 
Endogenous variables: Var1, Var2, Var3 
Deterministic variables: none 
Sample size: 499 
Log Likelihood: -2156.766 
Roots of the characteristic polynomial:
0.2846 0.2846 0.2306
Call:
VAR(y = df_sim, p = 1, type = "none")


Estimation results for equation Var1: 
===================================== 
Var1 = Var1.l1 + Var2.l1 + Var3.l1 

        Estimate Std. Error t value Pr(>|t|)    
Var1.l1  0.28806    0.05495   5.243 2.35e-07 ***
Var2.l1 -0.01945    0.04981  -0.390    0.696    
Var3.l1 -0.02626    0.04143  -0.634    0.526    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.9751 on 496 degrees of freedom
Multiple R-Squared: 0.08367,    Adjusted R-squared: 0.07812 
F-statistic:  15.1 on 3 and 496 DF,  p-value: 2.043e-09 


Estimation results for equation Var2: 
===================================== 
Var2 = Var1.l1 + Var2.l1 + Var3.l1 

        Estimate Std. Error t value Pr(>|t|)    
Var1.l1  0.07934    0.06634   1.196    0.232    
Var2.l1  0.29294    0.06015   4.871  1.5e-06 ***
Var3.l1 -0.04141    0.05002  -0.828    0.408    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 1.177 on 496 degrees of freedom
Multiple R-Squared: 0.09664,    Adjusted R-squared: 0.09118 
F-statistic: 17.69 on 3 and 496 DF,  p-value: 6.366e-11 


Estimation results for equation Var3: 
===================================== 
Var3 = Var1.l1 + Var2.l1 + Var3.l1 

        Estimate Std. Error t value Pr(>|t|)    
Var1.l1  0.03880    0.07597   0.511  0.60981    
Var2.l1  0.02380    0.06888   0.346  0.72984    
Var3.l1  0.21076    0.05728   3.679  0.00026 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 1.348 on 496 degrees of freedom
Multiple R-Squared: 0.04779,    Adjusted R-squared: 0.04203 
F-statistic: 8.297 on 3 and 496 DF,  p-value: 2.15e-05 



Covariance matrix of residuals:
        Var1   Var2    Var3
Var1  0.9489 0.4697 -0.2843
Var2  0.4697 1.3798  0.7335
Var3 -0.2843 0.7335  1.8061

Correlation matrix of residuals:
        Var1   Var2    Var3
Var1  1.0000 0.4105 -0.2172
Var2  0.4105 1.0000  0.4647
Var3 -0.2172 0.4647  1.0000

この段階では、変数の「過去の値（ラグ）」が現在に与える影響は推定されていますが、「同時点の因果関係」はまだ残差の相関の中に埋もれている状態です。

ダイナミクス（過去からの影響）の推定精度

各方程式の Estimate（係数推定値）を、シミュレーションで設定した真の係数行列 A1_true と比較します。

Var1の方程式:

Var1.l1 (0.288): 真の値は 0.4 です。やや低めに出ましたが、p値は設定した有意水準を下回っています。
他変数のラグ係数は棄却されず、真の構造（Var1は過去のVar1のみに依存）とおおむね整合的です。

Var2の方程式:

Var2.l1 (0.293): 真の値 0.3 とほぼ一致しており、有意です。
Var1.l1 (0.079) は有意になりませんでしたが、真の値は 0.1 と小さかったため、ノイズに埋もれた可能性があります。

Var3の方程式:

Var3.l1 (0.211): 真の値 0.2 とほぼ一致しており、有意です。

全体として、係数の推定値に多少のばらつきはあるものの、「各変数は自身の過去の値に強く依存している（対角要素が有意）」という真の動的構造をおおむね捉えています。

残差の相関（Correlation matrix of residuals）

残差間の相関行列を確認します。

        Var1   Var2    Var3
Var1  1.0000 0.4105 -0.2172
Var2  0.4105 1.0000  0.4647
Var3 -0.2172 0.4647  1.0000

Var1 と Var2 の間に 約 0.41 の相関があり、Var2 と Var3 の間には 約 0.46 の相関があります。

これは、「同時点において、変数同士が互いに連動している」ことを示しています。しかし、この「誘導形VAR」の結果だけでは、

「Var1 が動いたから Var2 が動いた」のか？
「Var2 が動いたから Var1 が動いた」のか？
「未知の第3の要因で両方が動いた」のか？

を区別できません。

シミュレーション設定（真の構造 \(B\) 行列）では、以下の因果関係が存在します。

Var1のショック \(\rightarrow\) Var2に波及
Var1とVar2のショック \(\rightarrow\) Var3に波及

上記の残差相関（0.41 や 0.46）は、この「真の因果関係」によって生じたものです。

通常のVARモデルでは、この相関を単なる「雑音の共変動」として処理してしまいます。

それゆえ、この相関関係を「構造的な因果（誰が誰に影響したか）」へと分解するために、SVAR 関数による識別（制約付き推定） を行います。

手順2: SVARモデルの識別と推定

# B行列の制約 (再帰的構造: 下三角行列)
Bmat_res <- matrix(c(
  NA, 0, 0,
  NA, NA, 0,
  NA, NA, NA
), nrow = 3, byrow = TRUE)

# Bmat のみを指定します。
# これにより、自動的に "B-model" (A=単位行列) として処理されます。
svar_est <- SVAR(x = var_est, estmethod = "scoring", Bmat = Bmat_res)

print(summary(svar_est))


SVAR Estimation Results:
======================== 

Call:
SVAR(x = var_est, estmethod = "scoring", Bmat = Bmat_res)

Type: B-model 
Sample size: 499 
Log Likelihood: -2161.279 
Method: scoring 
Number of iterations: 6 

Estimated A matrix:
     Var1 Var2 Var3
Var1    1    0    0
Var2    0    1    0
Var3    0    0    1

Estimated B matrix:
        Var1   Var2 Var3
Var1  0.9751 0.0000 0.00
Var2  0.4852 1.0727 0.00
Var3 -0.2868 0.8215 1.03

Estimated standard errors for B matrix:
        Var1    Var2   Var3
Var1 0.03087 0.00000 0.0000
Var2 0.05042 0.03396 0.0000
Var3 0.05967 0.05293 0.0326

Covariance matrix of reduced form residuals (*100):
       Var1   Var2   Var3
Var1  95.08  47.31 -27.96
Var2  47.31 138.60  74.21
Var3 -27.96  74.21 181.78

推定されたB行列（Estimated B matrix）

この行列は、構造的ショック（\(\epsilon_1, \epsilon_2, \epsilon_3\)）が、各変数（Var1, Var2, Var3）に与える同時点のインパクトを表しています。

Var1への影響（第1行）

推定値: 0.9751 （ショック \(\epsilon_1\) の係数）
真の値: 1.0
ほぼ一致しています。

Var2への影響（第2行）

推定値: 0.4852 （\(\epsilon_1\) からの影響）, 1.0727 （\(\epsilon_2\) からの影響）
真の値: 0.5, 1.0
「Var1のショックがVar2に波及する（係数0.5）」という構造を、推定値 0.4852 と、ほぼ一致して捉えています。前のステップ（VAR）で観測された残差相関（0.41）の正体が、この「0.5の因果関係」であったことが明らかになりました。

Var3への影響（第3行）

推定値: -0.2868 （\(\epsilon_1\) から）, 0.8215 （\(\epsilon_2\) から）, 1.03 （\(\epsilon_3\) から）
真の値: -0.3, 0.8, 1.0
以下のとおり、ほぼ一致しています。
- 「Var1のショックはVar3を下げる（-0.3）」 \(\rightarrow\) 推定値 -0.287
- 「Var2のショックはVar3を上げる（0.8）」 \(\rightarrow\) 推定値 0.822

制約の遵守と識別（Zeros）

行列の上三角成分（対角線より右上）がすべて 0.0000 になっています。

これは、引数 Bmat で指定した「再帰的構造（Var2はVar1に影響しない、Var3はVar1,2に影響しない）」という制約が適用されていることを示します。

この制約があったからこそ、相関関係を因果関係として解くことができました。

推定精度（Standard Errors）

Estimated standard errors for B matrix を見ると、推定値（約0.5や0.8など）と比較して、標準誤差は概ね 0.03 ～ 0.06 と小さい範囲に収まっています。

結論

通常のVARモデルでは、変数が「互いになんとなく相関している（残差相関）」ことしか分かりませんでした。

しかし、SVAR 関数を用いることで、その相関を分解し：

「Var1の変化が原因で、Var2が動いた（係数0.5）」
「Var1はVar3を押し下げるが（-0.3）、Var2経由の間接効果やVar2自体のショック（0.8）はVar3を押し上げる」

といった、具体的な因果のメカニズム（数値）を明らかにすることができました。

以上です。

関数 SVAR とは

関数 SVAR の引数