Rの関数から ARMAacf {stats} を確認します。
関数 ARMAacf とは
ARMAacf は、ARMA(自己回帰移動平均)モデルの 理論的な自己相関関数 (ACF) または 偏自己相関関数 (PACF) を計算する関数です。
本関数は「データから相関係数を推定する」ものではなく、指定されたモデルのパラメータ(AR係数やMA係数)に基づき、そのプロセスの理論的相関構造を算出し、モデルの特性を理解したり、シミュレーションの理論的なベンチマークを作成したりする際に使用されます。
関数 ARMAacf の引数
args(ARMAacf)function (ar = numeric(), ma = numeric(), lag.max = r, pacf = FALSE)
NULL-
ar- AR(自己回帰)項の係数ベクトル。
- モデル式 \(X_t = \phi_1 X_{t-1} + \dots + \phi_p X_{t-p} + \epsilon_t + \dots\) における \(\phi\) の部分を指定します。
- デフォルト:
numeric()(AR項なし)。
-
ma- MA(移動平均)項の係数ベクトル。
- モデル式 \(X_t = \dots + \epsilon_t + \theta_1 \epsilon_{t-1} + \dots + \theta_q \epsilon_{t-q}\) における \(\theta\) の部分を指定します。
- デフォルト:
numeric()(MA項なし)。
-
lag.max- 計算するラグの最大値。
- 数値を指定します。デフォルトでは、AR係数とMA係数の数に基づいて必要な最小限のラグ数が設定されます。
-
pacf- 偏自己相関関数(PACF)を計算するかどうかの論理値。
- デフォルト:
FALSE(ACFを計算)。 - 詳細:
-
FALSEの場合:自己相関関数(ACF)を返します。ラグ0(値は常に1)から始まります。 -
TRUEの場合:偏自己相関関数(PACF)を返します。ラグ1から始まります。
-
シミュレーションコード
以下に、ARMAacf の機能を確認するためのシミュレーションコードを示します。
このシミュレーションでは、以下の手順を実行します。
- 理論値の計算:
-
ARMAacfを使用して、特定のARMAモデルが持つ「理論的自己相関」を計算します。
-
- データの生成:
- そのモデルに従う乱数データを
arima.simで生成します。
- そのモデルに従う乱数データを
- 標本値の計算:
- 生成されたデータから「標本自己相関」を計算します。
- 比較:
- 理論値(
ARMAacf)と標本値(シミュレーション結果)を重ねてプロットし、データ数が増えれば標本値が理論値に収束することを確認します。
- 理論値(
今回は、AR項とMA項の両方を持つ ARMA(1, 1) モデルを使用します。
# パッケージの読み込み
library(ggplot2)
# 乱数シードの固定
seed <- 20260202
set.seed(seed)
# 1. ARMAモデルのパラメータ設定
# モデル: X_t = 0.8 * X_{t-1} + e_t + 0.6 * e_{t-1}
# AR係数 (phi) = 0.8: 正の自己相関を持ち、徐々に減衰する性質
# MA係数 (theta) = 0.6: 直近のノイズの影響を残す性質
ar_coef <- 0.8
ma_coef <- 0.6
max_lag <- 20
cat("--- モデル設定 ---\n")
cat(sprintf("AR係数: %.1f\n", ar_coef))
cat(sprintf("MA係数: %.1f\n", ma_coef))
cat(sprintf("最大ラグ: %d\n\n", max_lag))
# 2. ARMAacf を用いた理論的ACFの計算
theoretical_acf <- ARMAacf(ar = ar_coef, ma = ma_coef, lag.max = max_lag, pacf = FALSE)
# 3. シミュレーションによるデータの生成
# サンプルサイズを大きくするほど、理論値に近づきます
n_sample <- 10000
simulated_data <- arima.sim(model = list(ar = ar_coef, ma = ma_coef), n = n_sample)
# ggplot2で扱うためにデータフレームへ変換
df_ts_viz <- data.frame(
Time = 1:length(simulated_data),
Value = as.numeric(simulated_data)
)
# 3.1. 全期間のプロット(定常性の確認)
# データ全体を表示し、平均や分散が時間によって変化していないかを確認します
p_full <- ggplot(df_ts_viz, aes(x = Time, y = Value)) +
geom_line(color = "steelblue", linewidth = 0.3) +
geom_hline(yintercept = 0, color = "black", linetype = "dashed") +
labs(
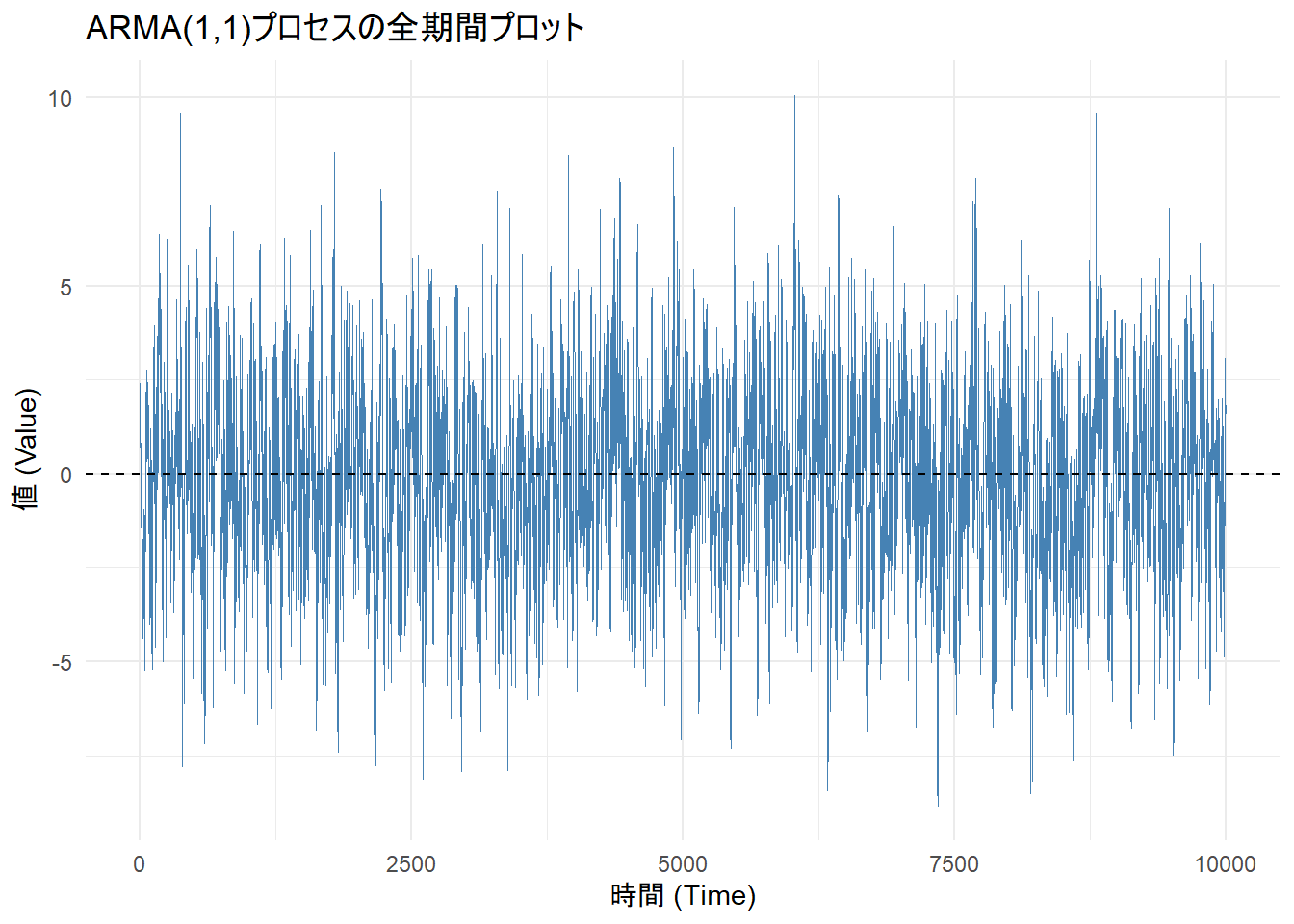
title = "ARMA(1,1)プロセスの全期間プロット",
x = "時間 (Time)",
y = "値 (Value)"
) +
theme_minimal()
print(p_full)
# 3.2. 最初の100時点の拡大プロット(挙動の確認)
# AR係数0.8の影響による「粘り気(前の値に引きずられる動き)」を確認します
p_zoom <- ggplot(df_ts_viz[1:100, ], aes(x = Time, y = Value)) +
geom_line(color = "darkblue", linewidth = 0.8) +
geom_point(size = 1.5, color = "darkblue", alpha = 0.6) +
geom_hline(yintercept = 0, color = "black", linetype = "dashed") +
labs(
title = "最初の100時点の拡大プロット",
x = "時間 (Time)",
y = "値 (Value)"
) +
theme_minimal()
print(p_zoom)--- モデル設定 ---
AR係数: 0.8
MA係数: 0.6
最大ラグ: 20Figure 1 からデータが0を中心に一定の幅(バンド)の中で推移していることが確認できます。
トレンド(右肩上がり等)や、発散(振幅がどんどん大きくなる)が見られないため、このデータは「定常(Stationary)」であると言えます。
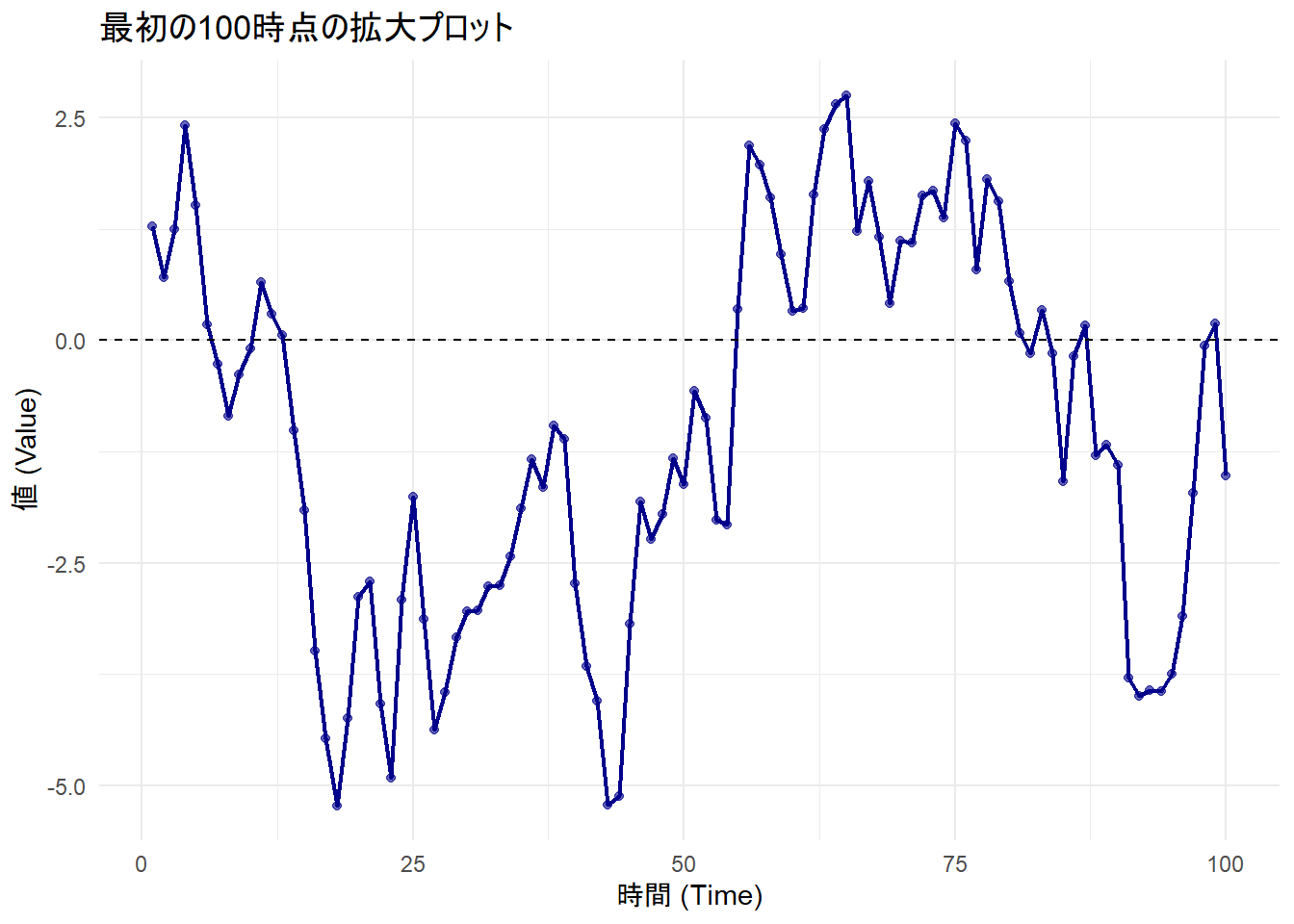
Figure 2 から、点を結ぶ線を見ると、ジグザグと激しく上下する(ホワイトノイズ的)というよりは、「一度上がるとしばらく高い位置に留まり、下がると低い位置に留まる」という波のような動きが見て取れます。
これが AR係数=0.8 による強い「正の自己相関」の視覚的な特徴です。
# 4. 標本ACFの計算
# 標本ACFの計算 (stats::acf 関数を使用)
# plot = FALSE にすることで数値データのみ取得
sample_acf_obj <- acf(simulated_data, lag.max = max_lag, plot = FALSE)
sample_acf_vals <- as.numeric(sample_acf_obj$acf)
# 5. データの結合と可視化
# データフレームの作成
df_compare <- data.frame(
Lag = 0:max_lag,
Theoretical = as.numeric(theoretical_acf),
Sample = sample_acf_vals
)
# 数値の確認(最初の5ラグ分)
cat("--- 自己相関の比較(先頭5ラグ)---\n")
print(head(df_compare, 6))--- 自己相関の比較(先頭5ラグ)---
Lag Theoretical Sample
1 0 1.0000000 1.0000000
2 1 0.8931034 0.8920494
3 2 0.7144828 0.7139438
4 3 0.5715862 0.5756903
5 4 0.4572690 0.4667994
6 5 0.3658152 0.3822490Lag 0 は自分自身との相関なので、常に 1.0 になります。
Lag 1 以降、Theoretical(理論値)と Sample(標本値)が近い値を示しています。
# プロットによる可視化
# 棒グラフ: 標本ACF (実際のデータから計算された値)
# 折れ線・点: 理論ACF (ARMAacfで計算された理論的相関構造)
p1 <- ggplot(df_compare, aes(x = Lag)) +
# 標本ACF(棒グラフ)
geom_bar(aes(y = Sample, fill = "標本ACF (シミュレーション)"),
stat = "identity", width = 0.6, alpha = 0.6
) +
# 理論ACF(折れ線と点)
geom_line(aes(y = Theoretical, color = "理論ACF (ARMAacf)"),
linewidth = 1
) +
geom_point(aes(y = Theoretical, color = "理論ACF (ARMAacf)"),
size = 3
) +
# ゼロライン
geom_hline(yintercept = 0, color = "black", linewidth = 0.5) +
# 色の設定
scale_fill_manual(name = "", values = c("標本ACF (シミュレーション)" = "skyblue")) +
scale_color_manual(name = "", values = c("理論ACF (ARMAacf)" = "red")) +
# ラベル設定
labs(
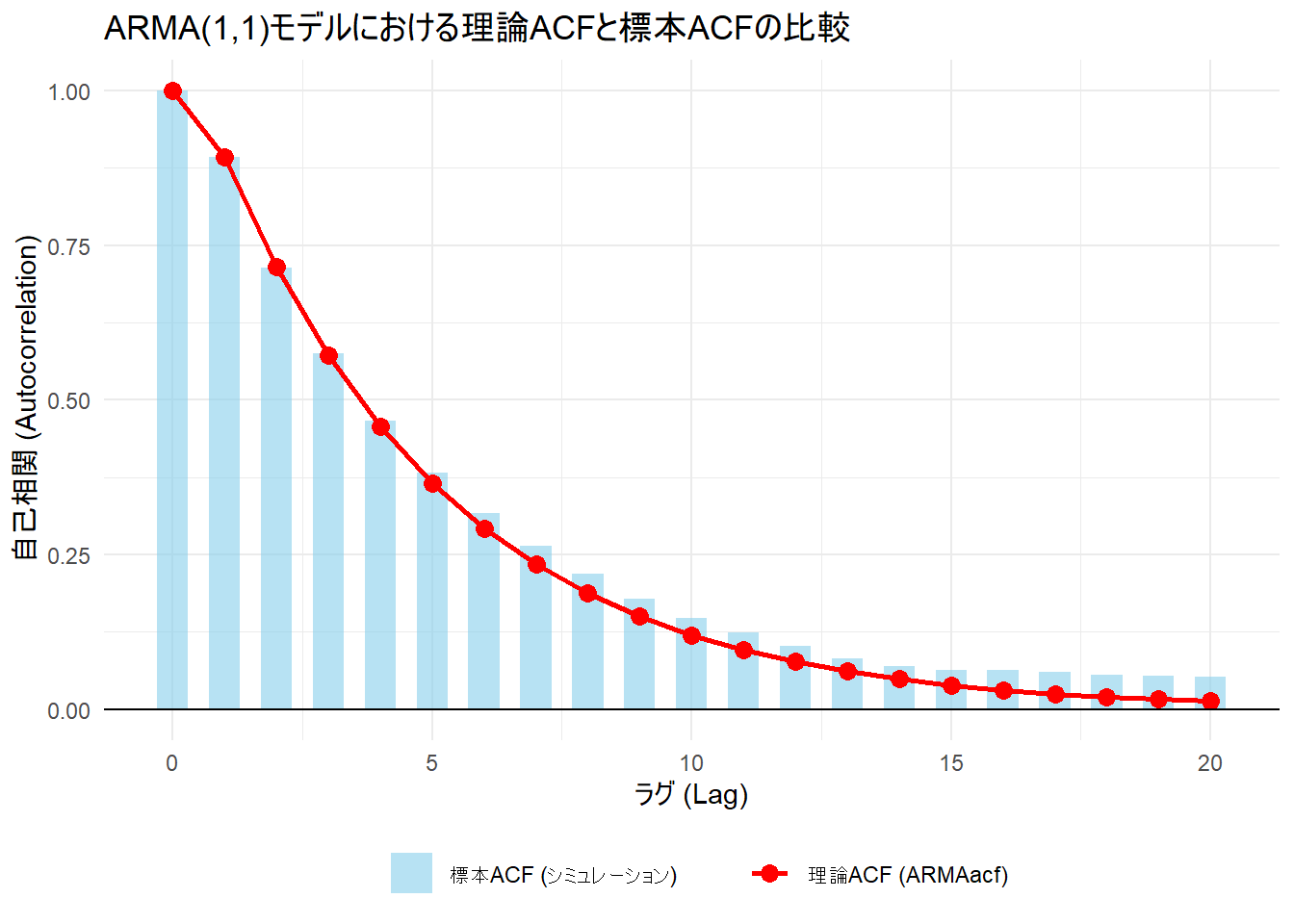
title = "ARMA(1,1)モデルにおける理論ACFと標本ACFの比較",
x = "ラグ (Lag)",
y = "自己相関 (Autocorrelation)"
) +
theme_minimal() +
theme(legend.position = "bottom")
print(p1)Figure 3 から、関数 ARMAacf で計算された理論値(赤線)に、シミュレーション結果(青棒)が従っていること様子が見られ、関数 ARMAacf は、ARMAモデルの理論的な性質を捉えていることが確認できます。
以上です。