Rの関数から Box.test {stats} を確認します。
関数 Box.test とは
Box.test は、時系列データにおける 自己相関の有無 を検定するための関数です。
特定のラグ(遅れ)単体ではなく、ラグ \(1\) からラグ \(k\) までの自己相関全体をまとめて評価するため、「Portmanteau検定」の一種に分類されます。
主に、時系列モデル(ARIMAなど)を当てはめた後の残差(residuals)がホワイトノイズ(無相関な雑音)になっているかどうかを確認する診断目的で使用されます。
帰無仮説(\(H_0\))は「データは独立である(自己相関を持たない)」であり、対立仮説(\(H_1\))は「データは独立ではない(有意な自己相関を持つ)」となります。
関数 Box.test の引数
args(Box.test)function (x, lag = 1, type = c("Box-Pierce", "Ljung-Box"), fitdf = 0)
NULL-
x- 検定対象となる数値ベクトルまたは単変量時系列オブジェクト。
-
lag- 検定に用いるラグの最大数(整数)。
- デフォルト:
1。 - どこまでの過去の影響を考慮するかを決定します。この値が小さいと長期的な相関を見逃す可能性があり、大きすぎると検定の検出力が低下する可能性があります。
-
type- 検定統計量の種類を指定する文字列。
- 選択肢:
-
"Box-Pierce"(デフォルト): 漸近的にカイ二乗分布に従います。 -
"Ljung-Box": 小標本(サンプルサイズが小さい場合)における近似精度を改善した検定統計量です。
-
- コード上の処理:
- Box-Pierce統計量: \(Q = n \sum_{k=1}^{h} \hat{\rho}_k^2\)
- Ljung-Box統計量: \(Q = n(n+2) \sum_{k=1}^{h} \frac{\hat{\rho}_k^2}{n-k}\)
- ここで \(n\) はサンプルサイズ、\(\hat{\rho}_k\) はラグ \(k\) の自己相関係数。
-
fitdf- 自由度の調整値(整数)。
- デフォルト:
0。 -
xが生データではなく、ARMAモデルなどの「推定された残差」である場合に使用します。モデルの推定に使用されたパラメータ数(\(p+q\))をここに指定することで、検定の自由度がlag - fitdfに調整されます。
シミュレーションコード
以下に、Box.test の機能を確認するためのサンプルデータを用いたシミュレーションコードを示します。
本シミュレーションでは、以下の2種類のデータを生成し、検定結果の違いを確認します。
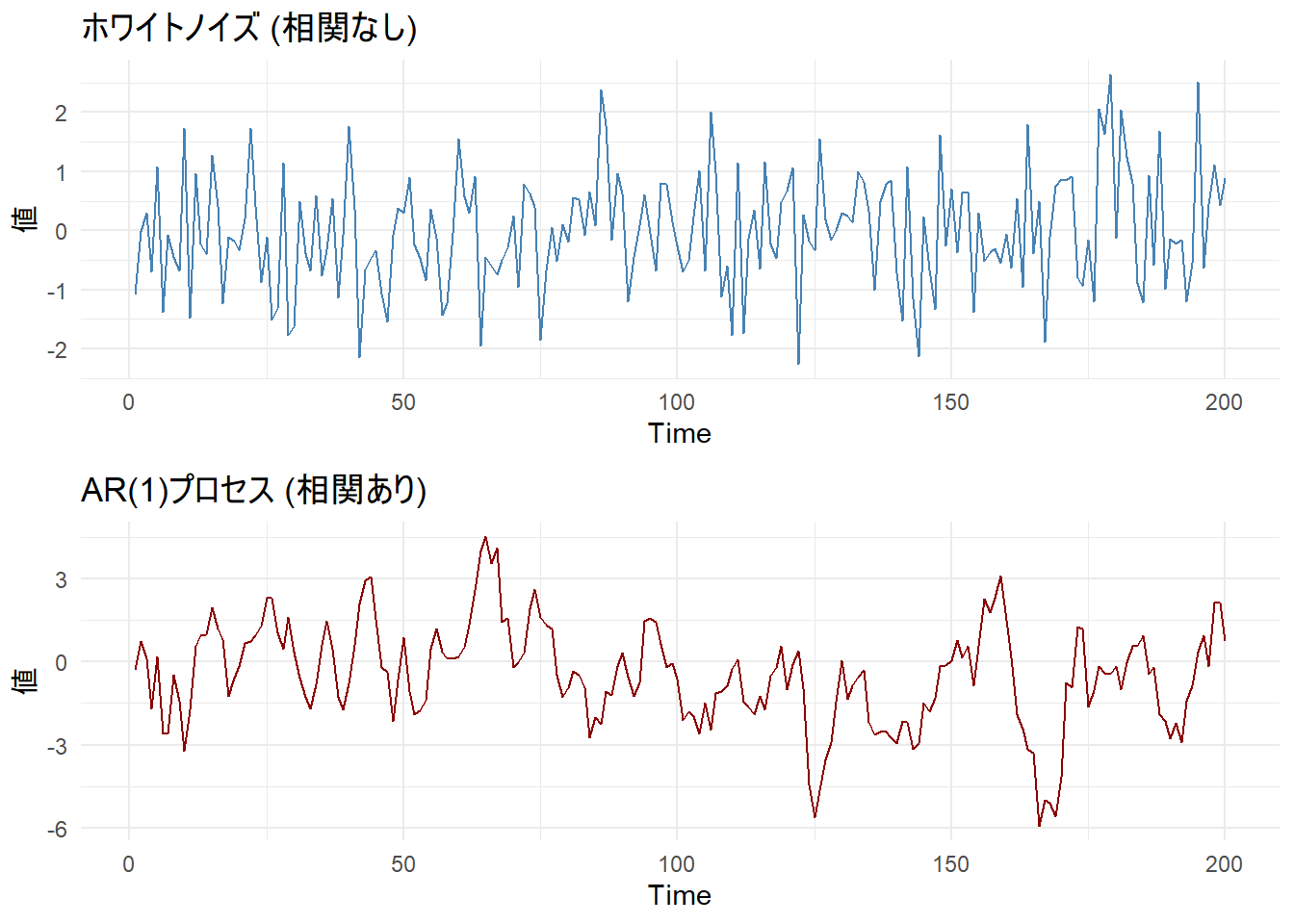
- ホワイトノイズ:
- 完全にランダムなデータ(自己相関なし)。
- 自己回帰プロセス (AR1):
- 過去の値に依存するデータ(自己相関あり)。
Box.test が、前者を「相関なし(帰無仮説を棄却しない)」、後者を「相関あり(帰無仮説を棄却する)」と正しく判定できるかを検証します。
なお、有意水準は5%とします。
サンプルデータの作成
# パッケージの読み込み
library(ggplot2)
library(gridExtra)
# 乱数シードの固定
seed <- 20260207
set.seed(seed)
# 1. サンプルデータの生成
n_sample <- 200
# シナリオA: ホワイトノイズ (White Noise)
# 正規分布に従う独立な乱数。自己相関は持たないはずである。
data_wn <- rnorm(n_sample)
# シナリオB: 自己回帰プロセス (Autoregressive Process)
# 直前の値に強く依存するデータ (AR係数 = 0.8)。自己相関を持つ。
# X_t = 0.8 * X_{t-1} + e_t
data_ar <- arima.sim(model = list(ar = 0.8), n = n_sample)
# データフレーム化(可視化用)
df_sim <- data.frame(
Time = 1:n_sample,
WhiteNoise = data_wn,
AR_Process = as.numeric(data_ar)
)
# 2. 時系列プロットによる確認
p1 <- ggplot(df_sim, aes(x = Time, y = WhiteNoise)) +
geom_line(color = "steelblue", linewidth = 0.5) +
labs(title = "ホワイトノイズ (相関なし)", y = "値") +
theme_minimal()
p2 <- ggplot(df_sim, aes(x = Time, y = AR_Process)) +
geom_line(color = "darkred", linewidth = 0.5) +
labs(title = "AR(1)プロセス (相関あり)", y = "値") +
theme_minimal()
grid.arrange(p1, p2, ncol = 1)検定結果: ホワイトノイズ
# 3. Box.test の実行 (Ljung-Box検定)
# 検定設定: ラグ10までの相関をチェックする
test_lag <- 10
cat("--- Box-Pierce ---\n")
print(Box.test(data_wn, lag = test_lag, type = "Box-Pierce"))
cat("--- Ljung-Box ---\n")
print(Box.test(data_wn, lag = test_lag, type = "Ljung-Box"))--- Box-Pierce ---
Box-Pierce test
data: data_wn
X-squared = 8.5472, df = 10, p-value = 0.5755
--- Ljung-Box ---
Box-Ljung test
data: data_wn
X-squared = 8.9181, df = 10, p-value = 0.5399どちらの検定タイプでも、P値が 設定した有意水準を上回っており、帰無仮説(自己相関なし)を棄却できません。
検定対象はホワイトノイズですので、正しく検定されています。
検定結果: AR(1)プロセス
cat("--- Box-Pierce ---\n")
print(Box.test(data_ar, lag = test_lag, type = "Box-Pierce"))
cat("--- Ljung-Box ---\n")
print(Box.test(data_ar, lag = test_lag, type = "Ljung-Box"))--- Box-Pierce ---
Box-Pierce test
data: data_ar
X-squared = 257.83, df = 10, p-value < 2.2e-16
--- Ljung-Box ---
Box-Ljung test
data: data_ar
X-squared = 262.76, df = 10, p-value < 2.2e-16どちらの検定タイプでも、P値が 設定した有意水準を下回っており、帰無仮説(自己相関なし)は棄却されます。
検定対象はAR(1)過程ですので、こちらも正しく検定されています。
自己相関関数の可視化
# 4. 自己相関関数 (ACF) の可視化
# ACFデータの取得
acf_wn <- acf(data_wn, plot = FALSE, lag.max = test_lag)
acf_ar <- acf(data_ar, plot = FALSE, lag.max = test_lag)
# データフレーム作成
df_acf <- rbind(
data.frame(Lag = acf_wn$lag[-1], ACF = acf_wn$acf[-1], Type = "ホワイトノイズ"),
data.frame(Lag = acf_ar$lag[-1], ACF = acf_ar$acf[-1], Type = "AR(1)プロセス")
)
# 信頼区間の計算 (近似的に 1.96 / sqrt(n))
ci_bound <- 1.96 / sqrt(n_sample)
p3 <- ggplot(df_acf, aes(x = Lag, y = ACF, fill = Type)) +
geom_bar(stat = "identity", position = "dodge", width = 0.6) +
geom_hline(yintercept = c(ci_bound, -ci_bound), linetype = "dashed", color = "blue") +
geom_hline(yintercept = 0, color = "black") +
facet_wrap(~Type) +
labs(
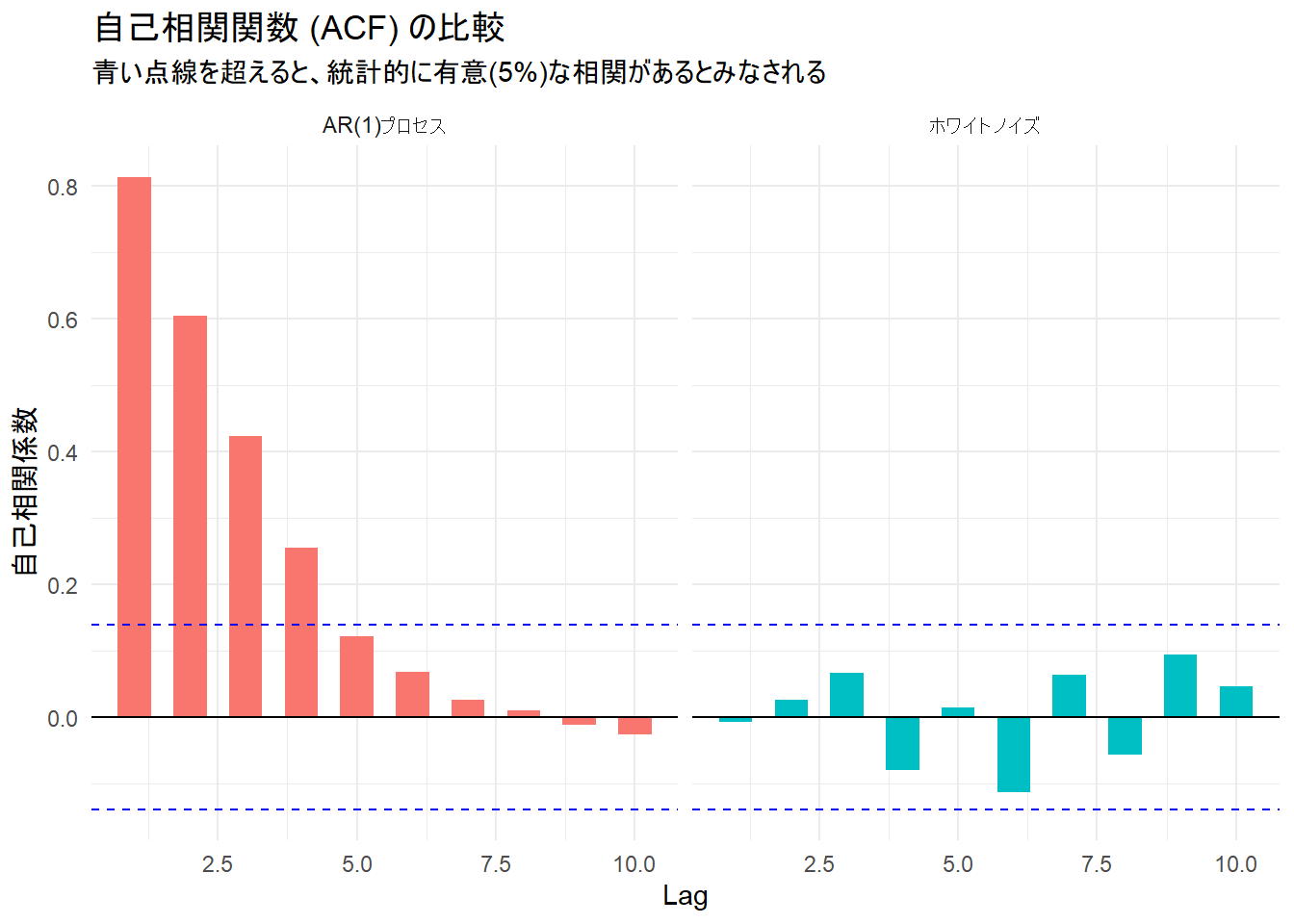
title = "自己相関関数 (ACF) の比較",
subtitle = "青い点線を超えると、統計的に有意(5%)な相関があるとみなされる",
y = "自己相関係数"
) +
theme_minimal() +
theme(legend.position = "none")
print(p3)検定統計量の手計算による算出
set.seed(seed)
# 1. データの準備
# サンプルサイズ n=200 の AR(1)プロセス
n <- 200
x <- arima.sim(model = list(ar = 0.8), n = n)
# 検定するラグ数
h <- 10
# 2. Rの関数 Box.test による計算
res_builtin <- Box.test(x, lag = h, type = "Ljung-Box")
q_stat_builtin <- res_builtin$statistic
cat("--- 関数 Box.test による検定統計量 ---\n")
cat(sprintf("X-squared = %.5f\n\n", q_stat_builtin))
# 3. 手計算による再現 (加重合計の実装)
# (A) 自己相関係数 (ACF) の取得
# acf関数は lag=0 (値は1) から返すため、必要な lag=1~h を取り出します
acf_obj <- acf(x, lag.max = h, plot = FALSE)
rho <- acf_obj$acf[2:(h + 1)] # lag 1 to h
# (B) 重み (Weight) の計算
# 公式: n * (n + 2) / (n - k)
# k は 1 から h までのラグ番号
k <- 1:h
weights <- (n * (n + 2)) / (n - k)
# (C) 加重合計の計算
# Q = sum( 重み * ACFの二乗 )
squared_acf <- rho^2
weighted_terms <- weights * squared_acf
q_stat_manual <- sum(weighted_terms)
# 4. 結果の比較表示
cat("--- 手計算による検定統計量 ---\n")
df_calc <- data.frame(
Lag_k = k,
ACF_sq = round(squared_acf, 5),
Weight = round(weights, 3),
Term = round(weighted_terms, 3) # Weight * ACF_sq
)
print(df_calc)
cat(sprintf("X-squared = %.5f\n\n", q_stat_manual))--- 関数 Box.test による検定統計量 ---
X-squared = 482.60180
--- 手計算による検定統計量 ---
Lag_k ACF_sq Weight Term
1 1 0.69866 203.015 141.839
2 2 0.47717 204.040 97.363
3 3 0.33696 205.076 69.102
4 4 0.23737 206.122 48.928
5 5 0.16046 207.179 33.243
6 6 0.10750 208.247 22.387
7 7 0.09963 209.326 20.856
8 8 0.08444 210.417 17.767
9 9 0.08132 211.518 17.202
10 10 0.06544 212.632 13.914
X-squared = 482.60180小標本におけるリュング・ボックス検定とボックス-ピアース検定の比較
シミュレーションの設計
- 条件:
- サンプルサイズを \(N=20\) と意図的に小さな値に設定します。
- データ生成:
- ケース1(帰無仮説が真):
- ホワイトノイズ。本来は「有意ではない」となるべきです。
- ケース2(対立仮説が真):
- 自己相関を持つAR(1)プロセス。本来は「有意である(相関がある)」と判定されるべきです。
- ケース1(帰無仮説が真):
- 比較:
- 同じデータに対して
Box-PierceとLjung-Boxを実行し、「偽陽性率(Type I Error)」と「検出力 (Power)」を比較します。
- 同じデータに対して
# パッケージの読み込み
library(tidyr)
library(dplyr)
# 乱数シードの固定
set.seed(seed)
# --- パラメータ設定 ---
n_small <- 20 # サンプルサイズ
n_sim <- 5000 # シミュレーション回数
test_lag <- 5 # 検定するラグ数
alpha <- 0.05 # 有意水準
# 結果格納用のデータフレーム
results <- data.frame(
Simulation_ID = 1:n_sim,
BP_Pval_WN = NA, # White Noise に対する Box-Pierce のP値
LB_Pval_WN = NA, # White Noise に対する Ljung-Box のP値
BP_Pval_AR = NA, # AR(1) に対する Box-Pierce のP値
LB_Pval_AR = NA # AR(1) に対する Ljung-Box のP値
)
# --- シミュレーション実行 ---
for (i in 1:n_sim) {
# 1. ホワイトノイズの生成 (相関なし)
wn_data <- rnorm(n_small)
# 2. AR(1)プロセスの生成 (相関あり: 係数 0.5)
# nが小さいと arima.sim は初期値の影響を受けやすいため、多めに作って捨てる
ar_data_full <- arima.sim(model = list(ar = 0.5), n = n_small + 50)
ar_data <- tail(ar_data_full, n_small)
# 3. 検定の実行
# ホワイトノイズに対して
bp_wn <- Box.test(wn_data, lag = test_lag, type = "Box-Pierce")
lb_wn <- Box.test(wn_data, lag = test_lag, type = "Ljung-Box")
# AR(1)データに対して
bp_ar <- Box.test(ar_data, lag = test_lag, type = "Box-Pierce")
lb_ar <- Box.test(ar_data, lag = test_lag, type = "Ljung-Box")
# P値を記録
results$BP_Pval_WN[i] <- bp_wn$p.value
results$LB_Pval_WN[i] <- lb_wn$p.value
results$BP_Pval_AR[i] <- bp_ar$p.value
results$LB_Pval_AR[i] <- lb_ar$p.value
}
# --- 結果の集計 ---
# 1. 有意水準(0.05)を下回った割合を計算
summary_table <- data.frame(
Data_Type = c("ホワイトノイズ", "AR(1)プロセス"),
Measure = c("偽陽性率(Type I Error)", "検出力(Power)"),
Box_Pierce = c(
mean(results$BP_Pval_WN < alpha),
mean(results$BP_Pval_AR < alpha)
),
Ljung_Box = c(
mean(results$LB_Pval_WN < alpha),
mean(results$LB_Pval_AR < alpha)
)
)
knitr::kable(summary_table)| Data_Type | Measure | Box_Pierce | Ljung_Box |
|---|---|---|---|
| ホワイトノイズ | 偽陽性率(Type I Error) | 0.0260 | 0.0662 |
| AR(1)プロセス | 検出力(Power) | 0.1648 | 0.2692 |
偽陽性率(Type I Error) は Box-Pierceの方が0.05(5%)より離れており、検出力(Power) はLjung-Boxの方が高いシミュレーション結果になりました。
以上です。