Rの関数から KalmanLike {stats} を確認します。
関数 KalmanLike とは
KalmanLike は、状態空間モデル(State Space Model)における「カルマンフィルタ(Kalman Filter)」を用いて、観測データに対するモデルの対数尤度(Log-Likelihood)を計算する関数です。
具体的には、時系列モデル(ARIMAや構造時系列モデルなど)のパラメータ推定において、あるパラメータ値が与えられたときに、そのモデルが観測データをどれくらい上手く説明できているかを数値化(尤度計算)するために使用されます。
内部ではC言語で実装されたカルマンフィルタのアルゴリズムが動作し、予測誤差分解(Prediction Error Decomposition)に基づいて尤度を算出します。
関数 KalmanLike の引数
args(KalmanLike)function (y, mod, nit = 0L, update = FALSE)
NULL-
y- 観測された時系列データ(一変量)。
- 数値ベクトルまたは時系列オブジェクト。
- 欠損値:
NAが含まれていても構いません(カルマンフィルタは欠損値を扱えるため)。
-
mod- 状態空間モデルの構造を定義したリスト。
- 必須要素:
-
Z: 観測行列(状態変数を観測値に変換する係数)。 -
a: 状態ベクトルの初期値(平均)。 -
P: 状態ベクトルの初期共分散行列。 -
T: 遷移行列(状態変数の時間発展を記述)。 -
V: 状態ノイズの共分散行列。 -
h: 観測ノイズの分散。 -
Pn: 状態共分散行列の更新用バッファ(初期値は通常Pと同じ)。
-
-
makeARIMA関数を使って作成することができます。
-
nit- 定常状態に達するまでの初期化期間として扱う観測数(整数)。
- デフォルト:
0L。
-
update- 計算後のモデルの状態(更新された
aやPなど)を属性として返すかどうかの論理値。 - デフォルト:
FALSE。 -
TRUEにすると、フィルタリング後の最終的な状態ベクトルや共分散行列を取得できます。
- 計算後のモデルの状態(更新された
返り値(出力)について
関数は以下の要素を持つリストを返します。
-
Lik:- 負の対数尤度(Negative Log-Likelihood)に関連する値。最適化関数(
optimなど)で最小化するための指標です。
- 負の対数尤度(Negative Log-Likelihood)に関連する値。最適化関数(
-
s2:- 予測誤差の分散(MLE推定値)。
シミュレーションコード
以下に、KalmanLike の機能を確認するためのサンプルデータを用いたシミュレーションコードを示します。
KalmanLike は、入力された分散パラメータの「絶対値」ではなく「比率」に基づいてフィルタリングを行い、全体のスケール(s2)を事後的に算出します。
よって、「分散比(Signal-to-Noise Ratio)」を最適化してから絶対値を復元する以下の手順でシミュレーションを行います。
- データの生成 (真の構造)
- モデル: ローカルレベルモデル(ランダムウォークする状態+観測ノイズ)。
- 真のパラメータ:
- 状態ノイズの分散 (\(\sigma_w^2\)): 1.0
- 観測ノイズの分散 (\(\sigma_v^2\)): 4.0
- 真の分散比: \(1.0 / 4.0 = \mathbf{0.25}\)
- パラメータに基づき、2000時点のデータを生成します。
- 最適化のための目的関数定義
-
optim関数で探索させるパラメータを「分散の絶対値」ではなく「分散比(ratio)」に限定します。 -
KalmanLikeに渡すモデルでは、観測ノイズ分散 \(h\) を1.0に固定し、状態ノイズ分散 \(V\) にratioを設定します。
-
- 最尤推定の実行
-
KalmanLikeが返すLik(負の対数尤度)が最小になるようなratioを探索します。
-
- パラメータの復元
- 最適化で得られた
est_ratioを使い、再度KalmanLikeを実行してs2(予測誤差分散のスケール因子) を取得します。 - この
s2が、固定していた観測ノイズ分散(\(1.0\))に対する倍率、つまり「実際の観測ノイズ分散」になります。 - 状態ノイズ分散は
s2 * est_ratioで計算されます。
- 最適化で得られた
# 乱数シード固定
seed <- 20260213
set.seed(seed)
# 分散比の推定精度検証
# 1. データの生成 (N=2000)
n_obs <- 2000
true_sigma_w <- 1.0 # 状態ノイズの標準偏差
true_sigma_v <- 2.0 # 観測ノイズの標準偏差
# 真の分散比 (Signal-to-Noise Ratio)
# ratio = sigma_w^2 / sigma_v^2 = 1.0 / 4.0 = 0.25
true_ratio <- (true_sigma_w^2) / (true_sigma_v^2)
# データの生成プロセス
w <- rnorm(n_obs, mean = 0, sd = true_sigma_w)
alpha <- cumsum(w)
v <- rnorm(n_obs, mean = 0, sd = true_sigma_v)
y <- alpha + v
cat(sprintf("真の分散比 (w/v): %.2f\n", true_ratio))
cat(sprintf("真の状態ノイズ分散: %.2f\n", true_sigma_w^2))
cat(sprintf("真の観測ノイズ分散: %.2f\n\n", true_sigma_v^2))
# サンプルデータの可視化
# パッケージ読み込み
library(ggplot2)
# 可視化用データフレームの作成
df_viz <- data.frame(
Time = 1:length(y),
Observed = y, # 観測値 (y)
State = alpha # 真の状態 (alpha)
)
# 1. 全期間 (N=2000) の可視化
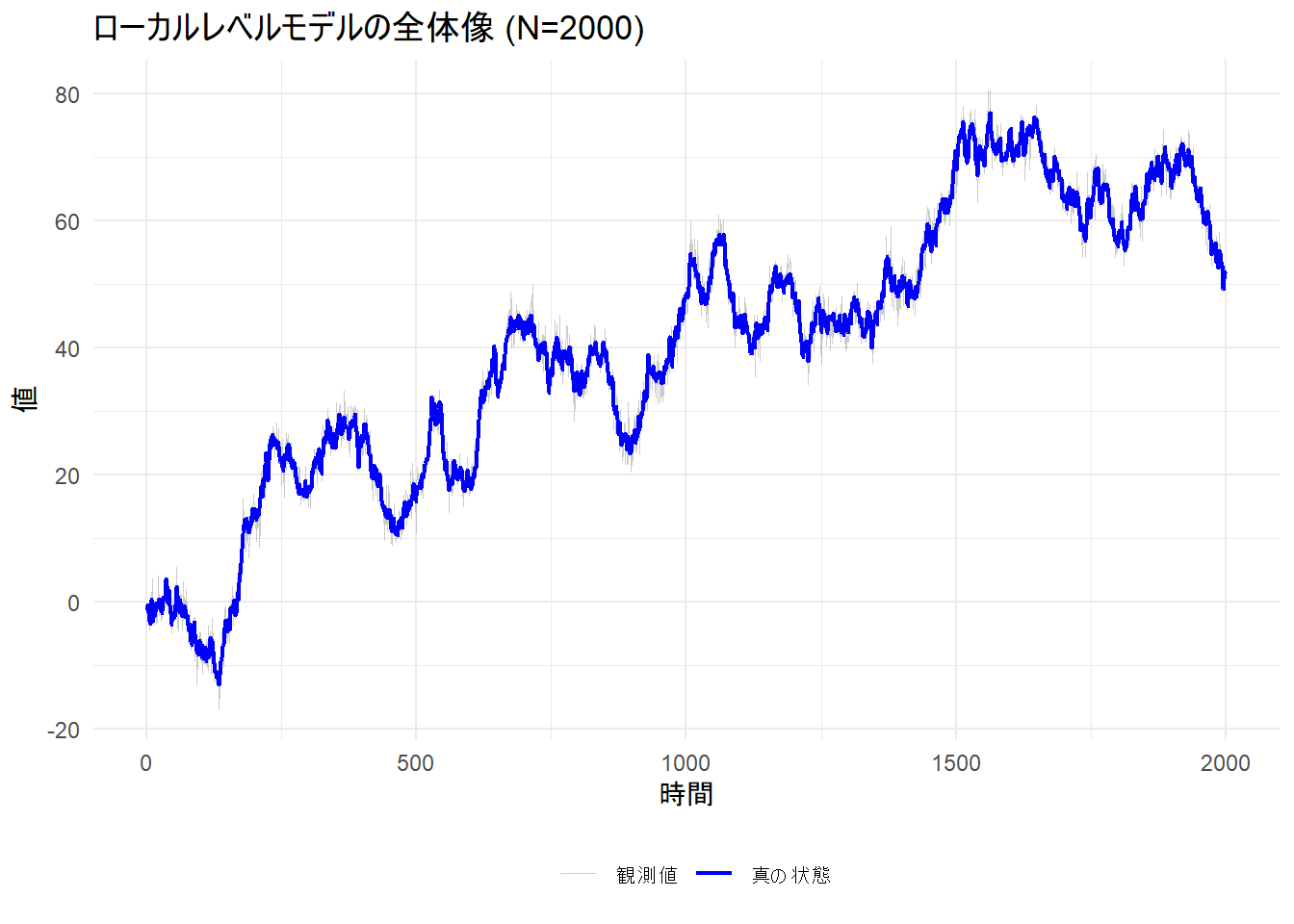
# 全体像:ランダムウォークにより大きく値が変動している様子
p1 <- ggplot(df_viz, aes(x = Time)) +
# 観測値(グレーで薄く表示)
geom_line(aes(y = Observed, color = "観測値"), alpha = 0.5, linewidth = 0.3) +
# 真の状態(青色ではっきり表示)
geom_line(aes(y = State, color = "真の状態"), linewidth = 0.8) +
scale_color_manual(
name = "",
values = c("観測値" = "gray60", "真の状態" = "blue")
) +
labs(
title = "ローカルレベルモデルの全体像 (N=2000)",
x = "時間", y = "値"
) +
theme_minimal() +
theme(legend.position = "bottom")
print(p1)
# 2. 拡大図 (最初の200時点)
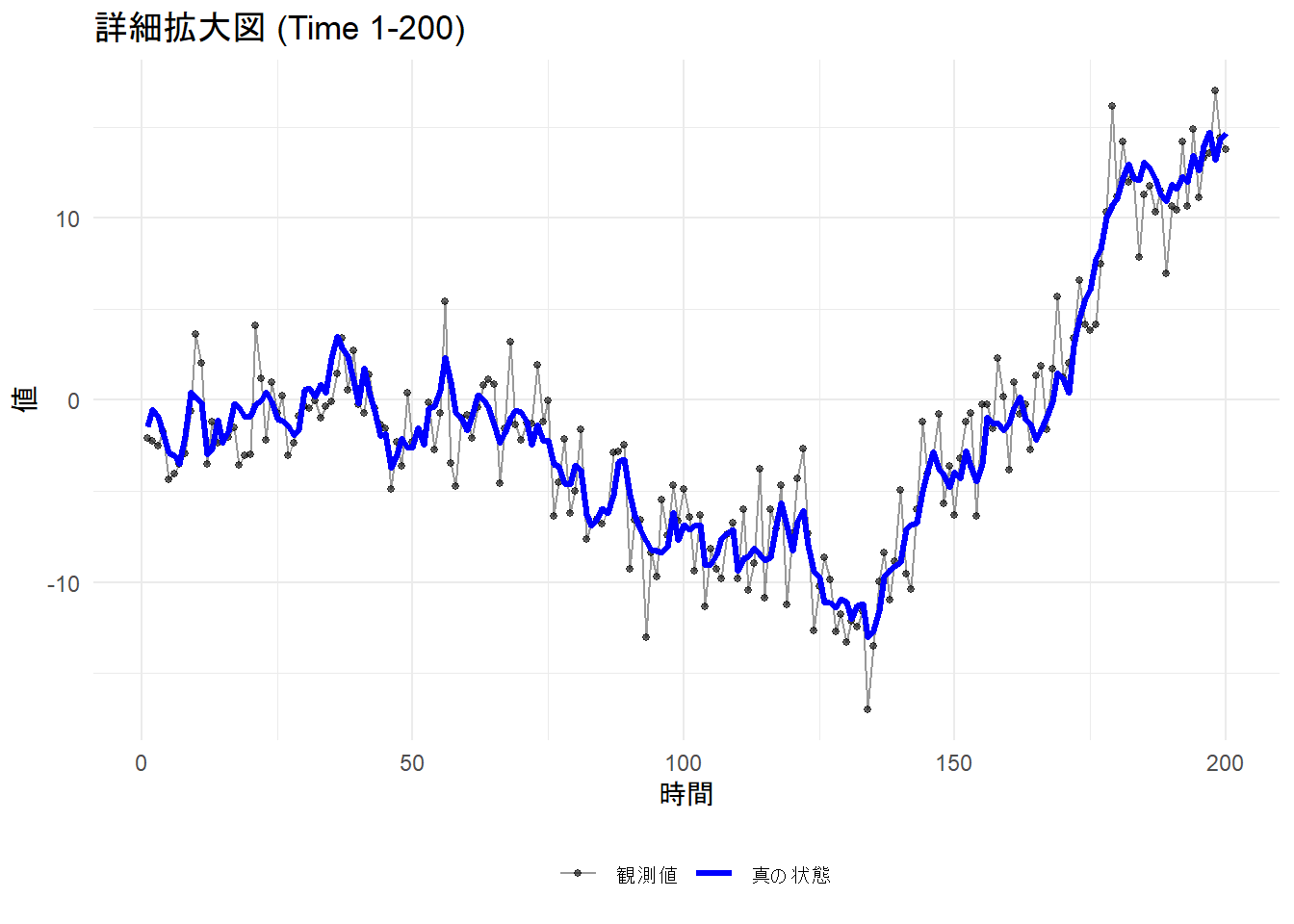
# 詳細:ノイズのばらつき具合を確認
p2 <- ggplot(df_viz[1:200, ], aes(x = Time)) +
# 観測値(点と線)
geom_line(aes(y = Observed, color = "観測値"), alpha = 0.4) +
geom_point(aes(y = Observed, color = "観測値"), size = 1, alpha = 0.6) +
# 真の状態(太い線)
geom_line(aes(y = State, color = "真の状態"), linewidth = 1.2) +
scale_color_manual(
name = "",
values = c("観測値" = "black", "真の状態" = "blue")
) +
labs(
title = "詳細拡大図 (Time 1-200)",
x = "時間", y = "値"
) +
theme_minimal() +
theme(legend.position = "bottom")
print(p2)真の分散比 (w/v): 0.25
真の状態ノイズ分散: 1.00
真の観測ノイズ分散: 4.00Figure 1 から、長期的に見ると観測値は真の状態(トレンド)に沿って推移している様子が、Figure 2 から、青線の滑らかな動き(状態分散=1)に対し、黒点は大きく散らばっている(観測分散=4)様子が確認できます。
# 2. モデル定義関数
make_local_level_mod <- function(y, sigma_w_sq, sigma_v_sq) {
mod <- list(
Z = matrix(1, 1, 1),
a = matrix(0, 1, 1),
P = matrix(10, 1, 1),
T = matrix(1, 1, 1),
V = matrix(sigma_w_sq, 1, 1),
h = sigma_v_sq,
Pn = matrix(10, 1, 1)
)
return(mod)
}
# 3. 最尤推定
# 目的関数: 分散比 (ratio) を探索
objective_fn_ratio <- function(par) {
ratio <- exp(par[1]) # 正の値に制約
# 観測ノイズ(h)を1に固定し、状態ノイズ(V)を比率として入力
# これにより、尤度計算のスケール不変性を回避します
mod <- make_local_level_mod(y, sigma_w_sq = ratio, sigma_v_sq = 1.0)
res <- KalmanLike(y, mod)
return(res$Lik)
}
# 最適化実行
# 初期値: log(0.1) -> 比率0.1程度からスタート
init_par_ratio <- c(log(0.1))
opt_res <- optim(init_par_ratio, objective_fn_ratio, method = "BFGS")
# 4. 結果の復元と出力
est_ratio <- exp(opt_res$par[1])
# 最適な比率を使って再度 KalmanLike を実行し、スケール因子(s2)を取得
final_mod <- make_local_level_mod(y, sigma_w_sq = est_ratio, sigma_v_sq = 1.0)
final_res <- KalmanLike(y, final_mod)
# 推定された分散値の計算
# 観測ノイズ分散 = s2 * 1.0 (hを1に固定したため)
est_v_sq <- final_res$s2
# 状態ノイズ分散 = s2 * 推定比率
est_w_sq <- final_res$s2 * est_ratio
cat("--- 推定結果の比較 ---\n")
cat(sprintf("推定された分散比 (w/v): %.4f (真の値: %.2f)\n", est_ratio, true_ratio))
cat(sprintf("推定 状態ノイズ分散 : %.4f (真の値: %.2f)\n", est_w_sq, true_sigma_w^2))
cat(sprintf("推定 観測ノイズ分散 : %.4f (真の値: %.2f)\n", est_v_sq, true_sigma_v^2))--- 推定結果の比較 ---
推定された分散比 (w/v): 0.2685 (真の値: 0.25)
推定 状態ノイズ分散 : 1.0839 (真の値: 1.00)
推定 観測ノイズ分散 : 4.0372 (真の値: 4.00)- 分散比 (\(w/v\)):
- 真の値 0.25 に対し、推定値は 0.2685 です。誤差は 0.02 程度であり、真の比率(シグナルとノイズのバランス)を捉えていると言えます。
- 状態ノイズ分散 (\(\sigma_w^2\)):
- 真の値 1.00 に対し、推定値は 1.0839 です。 こちらも真の値に近く、状態(トレンド)が刻一刻と変化していく度合いを学習できていると言えます。
- 観測ノイズ分散 (\(\sigma_v^2\)):
- 真の値 4.00 に対し、推定値は 4.0372 です。観測データのバラつきのうち、どれだけが「単なる測定誤差(ノイズ)」であるかを、モデルは捉えています。
参照コード
以上です。