Rの関数から NLSstClosestX {stats} を確認します。
関数 NLSstClosestX とは
NLSstClosestX は、非線形最小二乗法(NLS)の初期値推定において、「指定された \(y\) の値(yval)に対応する \(x\) の値を、データから逆算して推定する」ための関数です。
主に、ロジスティック曲線やゴンペルツ曲線などの Self-Starting Models の内部で使用されます。
例えば、ロジスティック曲線の変曲点(\(y\) が最大値の半分の値になる点)の \(x\) 座標を推定したい場合などに利用されます。
本関数は、単に最も近いデータ点を探すだけではなく、目的の yval がデータ点の間にある場合、その前後2点を用いて逆線形補間(Inverse Linear Interpolation)を行い、\(x\) の値を算出します。
関数 NLSstClosestX の引数
args(NLSstClosestX)function (xy, yval)
NULL本関数は S3 メソッドであり、sortedXyData クラスのオブジェクトに対して動作します。
-
xy- \(x\) と \(y\) のデータを含む
sortedXyDataクラスのオブジェクト。 -
stats::sortedXyData()関数を用いて作成された、xの昇順にソートされたデータ構造である必要があります。 -
xとyという列名を持ち、xでソートされていることが保証されています。
- \(x\) と \(y\) のデータを含む
-
yval- 探索対象となる \(y\) の値(ターゲット値)。
- 単一の数値(スカラー)。
- 「\(y\) がこの値になるときの \(x\) はいくつか?」という問いにおける「この値」を指定します。
内部アルゴリズムの挙動
# stats::NLSstClosestX の sortedXyData クラス用メソッド
# 引数 xy: sortedXyData オブジェクト(xでソートされたデータフレーム的なもの)
# 引数 yval: ターゲットとなる y の値(この値になるときの x を知りたい)
function(xy, yval) {
# 1. 偏差の計算
# データの各 y 値とターゲット値との差を計算する
# 負の値ならターゲットより下、正の値ならターゲットより上にデータがある
deviations <- xy$y - yval
# 2. 完全一致の判定
# もしデータの中にターゲットと完全に一致する y があれば、
# そのデータ点の x をそのまま返す(計算不要)
if (any(deviations == 0)) {
return(xy$x[match(0, deviations)])
}
# 3. 下側(ターゲットより小さい値)の直近点を探す
if (any(deviations <= 0)) {
# ターゲット以下の偏差の中で、最大のもの(=偏差が0に最も近い負の値)を探す
dev1 <- max(deviations[deviations <= 0])
# その偏差を持つデータ点の x 座標を取得 (これを x1 とする)
lim1 <- xy$x[match(dev1, deviations)]
# もし「全てのデータがターゲット以下」なら、補間できないため
# 最も近い点(最大のデータ点)の x をそのまま返す(端点処理)
if (all(deviations <= 0)) {
return(lim1)
}
}
# 4. 上側(ターゲットより大きい値)の直近点を探す
if (any(deviations >= 0)) {
# ターゲット以上の偏差の中で、最小のもの(=偏差が0に最も近い正の値)を探す
dev2 <- min(deviations[deviations >= 0])
# その偏差を持つデータ点の x 座標を取得 (これを x2 とする)
lim2 <- xy$x[match(dev2, deviations)]
# もし「全てのデータがターゲット以上」なら、補間できないため
# 最も近い点(最小のデータ点)の x をそのまま返す(端点処理)
if (all(deviations >= 0)) {
return(lim2)
}
}
# --- ここに来る時点で、ターゲットを挟む2点 (x1, y1) と (x2, y2) が特定されている ---
# dev1: y1 - yval (負の値)
# dev2: y2 - yval (正の値)
# 5. 距離の絶対値化
dev1 <- abs(dev1) # ターゲットから下の点までの距離 d1
dev2 <- abs(dev2) # ターゲットから上の点までの距離 d2
# 6. 逆線形補間 (Inverse Linear Interpolation) の実行
# 2点間を直線で結び、内分点の公式を使って x を推定する
# 式: x = x1 + (x2 - x1) * (d1 / (d1 + d2))
lim1 + (lim2 - lim1) * dev1 / (dev1 + dev2)
}シミュレーションコード
以下に、NLSstClosestX の機能を確認するためのサンプルデータを用いたシミュレーションコードを示します。
このシミュレーションでは、S字カーブ(ロジスティック曲線)を描くデータを生成します。
データ点は離散的(飛び飛び)ですが、NLSstClosestX を使うことで、データ点の間にある特定の \(y\) 値(例:最大値の50%)に対応する \(x\) を推定できることを確認します。
サンプルデータの作成
# パッケージの読み込み
library(ggplot2)
# NLSstClosestX 関数の理解:逆線形補間のシミュレーション
# 1. サンプルデータの生成
# ロジスティック曲線: y = Asym / (1 + exp((xmid - x) / scal))
# x=5 のとき y=5.0 (変曲点) となるロジスティック曲線とします。
# 生物学的な成長曲線などを模倣します。
# データ点はあえて「粗く(少なく)」して、補間の効果を見やすくします。
x_vals <- seq(0, 10, by = 1) # 0から10まで、1刻みの粗いデータ
true_Asym <- 10.0 # 最大値
true_xmid <- 5.0 # 変曲点(yが5.0になるx)
true_scal <- 1.5 # スケール(傾きの緩やかさ)
# y値の計算(ノイズなしの理想的なカーブ)
y_vals <- true_Asym / (1 + exp((true_xmid - x_vals) / true_scal))
# データフレーム化
df_sim <- data.frame(x = x_vals, y = y_vals)
# sortedXyData オブジェクトへの変換(必須)
xy_data <- sortedXyData(df_sim$x, df_sim$y)
cat("--- データ概要 ---\n")
cat("xの値:", paste(head(x_vals, 11), collapse = ", "), "\n")
cat("yの値:", paste(round(head(y_vals, 11), 2), collapse = ", "), "\n")--- データ概要 ---
xの値: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
yの値: 0.34, 0.65, 1.19, 2.09, 3.39, 5, 6.61, 7.91, 8.81, 9.35, 9.66 関数 NLSstClosestX の実効
シナリオA:データ点と完全に一致する場合
# 2. NLSstClosestX の実行
# シナリオA: データ点と完全に一致する場合
# x=5 のとき y=5.0 なので、yval=5.0 を与えれば x=5 が返るはずです
target_y_exact <- 5.0
est_x_exact <- NLSstClosestX(xy_data, target_y_exact)
cat("--- シナリオA: データ点上に解がある場合 ---\n")
cat(sprintf("ターゲット y: %.1f\n", target_y_exact))
cat(sprintf("推定された x: %.4f (正解: 5.0)\n\n", est_x_exact))--- シナリオA: データ点上に解がある場合 ---
ターゲット y: 5.0
推定された x: 5.0000 (正解: 5.0) シナリオB:データ点の間に解がある場合(補間の検証)
# シナリオB: データ点の間に解がある場合(補間の検証)
# y = 8.0 となる x を探します。
# データ上は x=6(y=6.68) と x=7(y=7.98) と x=8(y=8.80) の間にあります。
# ロジスティック式の逆関数で計算した真のxは、
# 8 = 10 / (1 + exp((5 - x)/1.5)) -> x = 5 - 1.5 * log(10/8 - 1)
true_x_for_8 <- 5.0 - 1.5 * log(10 / 8 - 1) # 約 7.079
target_y_interp <- 8.0
est_x_interp <- NLSstClosestX(xy_data, target_y_interp)
cat("--- シナリオB: データ点の間に解がある場合 ---\n")
cat(sprintf("ターゲット y: %.1f\n", target_y_interp))
cat("直近のデータ点: x=7 (y=7.98) と x=8 (y=8.81) の間\n")
cat(sprintf("推定された x: %.4f\n", est_x_interp))
cat(sprintf("真のモデル x: %.4f\n", true_x_for_8))--- シナリオB: データ点の間に解がある場合 ---
ターゲット y: 8.0
直近のデータ点: x=7 (y=7.98) と x=8 (y=8.81) の間
推定された x: 7.0963
真のモデル x: 7.0794単純な「最も近い点」ではなく、2点間を直線で結んで計算するため、真の値に近い(しかし曲線ではないため若干ずれる)値が算出されます。
可視化による確認
# 3. 可視化による確認
# 補間がどのように行われているかを図示します
# 補間に使用されたと思われる2点を特定(可視化用)
idx_lower <- which(df_sim$y < target_y_interp)
idx_upper <- which(df_sim$y >= target_y_interp)
p1_idx <- max(idx_lower) # y=8.0 の直下の点
p2_idx <- min(idx_upper) # y=8.0 の直上の点
# 補間線分データ
segment_data <- df_sim[c(p1_idx, p2_idx), ]
p1 <- ggplot(df_sim, aes(x = x, y = y)) +
# 全体のカーブ(点と線)
geom_line(color = "gray60", linewidth = 0.5) +
geom_point(size = 3, color = "black") +
# ターゲットYのライン
geom_hline(yintercept = target_y_interp, color = "blue", linetype = "dashed") +
annotate("text",
x = 0, y = target_y_interp + 0.2,
label = paste("Target y =", target_y_interp), color = "blue", hjust = 0
) +
# 補間に使われた2点間の直線(赤色)
geom_segment(
aes(
x = segment_data$x[1], y = segment_data$y[1],
xend = segment_data$x[2], yend = segment_data$y[2]
),
color = "red", linewidth = 1.2
) +
# NLSstClosestXが算出したポイント
geom_point(aes(x = est_x_interp, y = target_y_interp),
color = "red", size = 5, shape = 18
) +
# 垂線(x軸への)
geom_segment(
aes(
x = est_x_interp, xend = est_x_interp,
y = 0, yend = target_y_interp
),
color = "red", linetype = "dotted"
) +
labs(
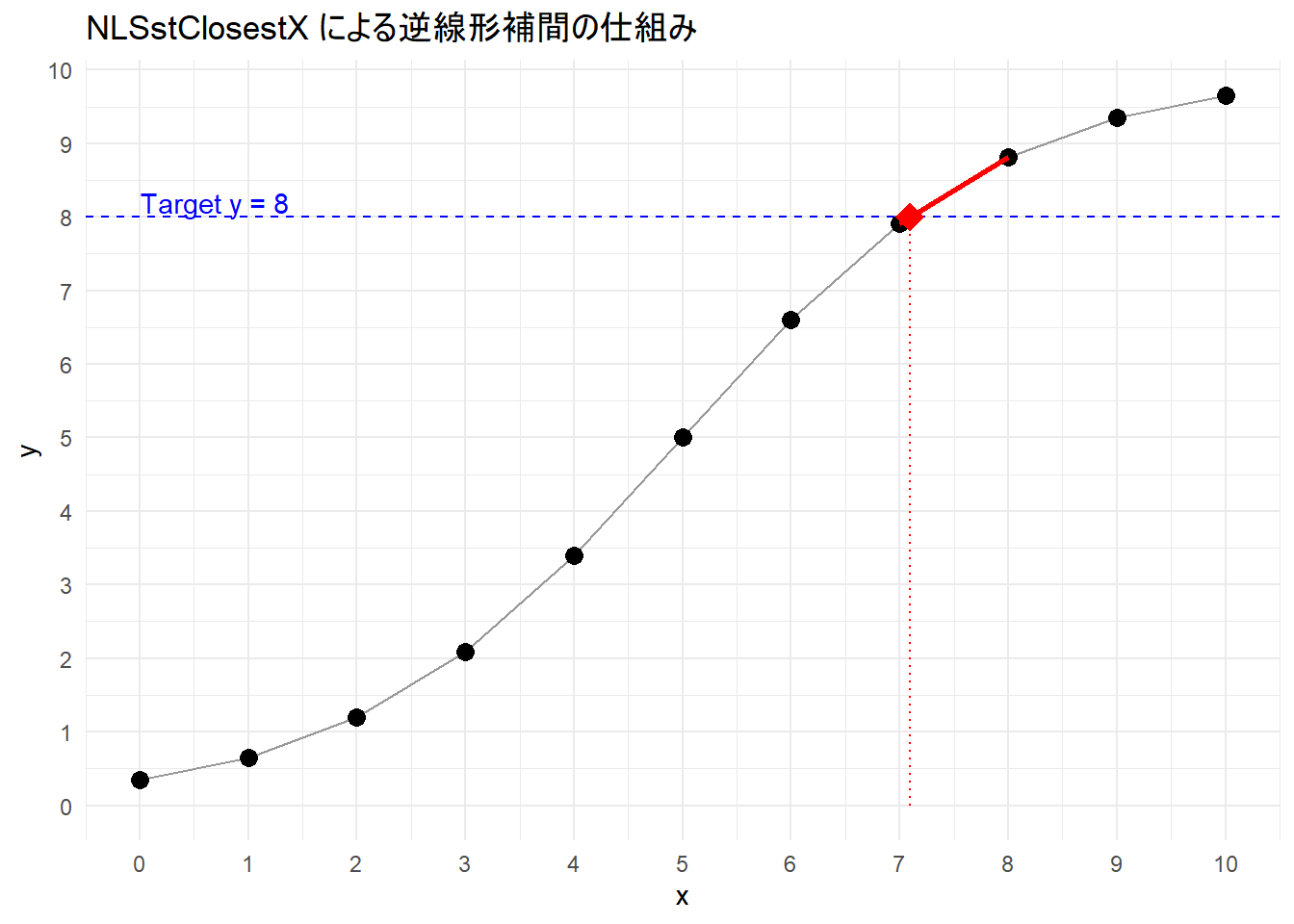
title = "NLSstClosestX による逆線形補間の仕組み",
x = "x", y = "y"
) +
theme_minimal() +
scale_x_continuous(breaks = 0:10) +
scale_y_continuous(breaks = 0:10)
print(p1)Figure 1 は、ターゲットy(青線)に対し、隣接する2点を結ぶ直線(赤実線)との交点(赤菱形)を求めている様子です。
関数 NLSstClosestX は、離散的なデータ点の間を「直線」でつなぐことで、任意の y に対応する x を推定します。
よって、非線形回帰の初期値推定において「曲線のパラメータ(中点など)」をデータから概算するための有効な手法になります。
以上です。