Rの関数:quantile {stats}

関数 quantile とは

quantile は、数値データのベクトルから、指定された確率に対応する 標本分位点（Sample Quantiles） を計算する関数です。

分位点はデータの分布特性（中心、広がり、歪みなど）を把握するために有用な統計量です。

例えば、0.5（50%）の分位点は中央値（メディアン）、0.25と0.75の分位点は四分位数に相当します。

理論的な母集団の分位点とは異なり、有限の標本から分位点を推定する方法には複数の定義が存在します。

本関数は、引数 type によって9種類の計算アルゴリズムが選択可能です。

関数 quantile の引数

args(getS3method("quantile", "default"))

function (x, probs = seq(0, 1, 0.25), na.rm = FALSE, names = TRUE, 
    type = 7L, digits = 7, fuzz = if (type == 7L) 0 else 4 * 
        .Machine$double.eps, ...) 
NULL

1. x
   • 分位点を計算したい数値ベクトル。
2. probs
   • 計算したい分位点の確率（0から1の範囲）。
   • デフォルト: seq(0, 1, 0.25)。すなわち、0%（最小値）、25%、50%（中央値）、75%、100%（最大値）の5点を計算します。
3. na.rm
   • 計算前に欠損値（NA）および非数（NaN）を除去するかどうかの論理値。
   • デフォルト: FALSE。FALSE の場合にデータに欠損が含まれているとエラーになります。
4. names
   • 結果のベクトルに名前（“25%” など）を付与するかどうかの論理値。
   • デフォルト: TRUE。
5. type
   • 分位点を計算するアルゴリズムの種類を指定する整数（1から9）。
   • デフォルト: 7。
   • 分類:
     • Type 1 ~ 3 (不連続): 階段関数（ステップ関数）として計算します。経験分布関数に基づきます。
     • Type 4 ~ 9 (連続): 順序統計量の間を線形補間します。
   • 各タイプの概要:
     • 1: 経験分布関数の逆関数（不連続）。
     • 2: 不連続点において平均をとる（不連続）。
     • 3: 最も近い偶数の順序統計量をとる。
     • 4: \(p_k = k / n\)。
     • 5: \(p_k = (k - 0.5) / n\)。
     • 6: \(p_k = k / (n + 1)\)。
     • 7 (デフォルト): \(p_k = (k - 1) / (n - 1)\)。データの範囲（レンジ）を確率 0～1 に線形にマッピングします。
     • 8: 推定量のバイアスを減らすために推奨される定義。\(p_k = (k - 1/3) / (n + 1/3)\)。
     • 9: 正規分布に対して不偏に近い定義。\(p_k = (k - 3/8) / (n + 1/4)\)。
6. digits
   • 結果の名前に付与されるパーセンテージの有効桁数。
   • デフォルト: 7。
7. fuzz
   • 数値計算上の誤差（浮動小数点誤差）を許容するための微小値。
8. ...
   • その他の引数。現在は names 属性のフォーマットに関する引数などを渡すために利用されます。

シミュレーションコード

以下に、quantile 関数の type 引数による挙動の違いを確認するためのシミュレーションコードを示します。

本シミュレーションでは、「標準正規分布からサイズ20のサンプルを抽出したとき、95%分位点（理論値は約1.645）を各タイプがどのように推定するか」を1000回繰り返し検証します。

サンプルサイズが小さい（\(N=20\)）場合、アルゴリズムの違いが推定結果に大きな影響を与えます。

どのタイプが理論値に対して過小評価、あるいは過大評価する傾向があるかを確認します。

# パッケージの読み込み
library(ggplot2)
library(dplyr)
library(tidyr)

# 乱数シードの固定
seed <- 20260210
set.seed(seed)

# quantile関数のアルゴリズム比較シミュレーション

# --- パラメータ設定 ---
N <- 20 # サンプルサイズ (小標本)
n_sim <- 1000 # シミュレーション回数
target_prob <- 0.95 # 比較する確率 (95%点)
true_quantile <- qnorm(target_prob) # 真の95%点 (約1.645)

cat(sprintf("サンプルサイズ: %d\n", N))
cat(sprintf("ターゲット確率: %.2f\n", target_prob))
cat(sprintf("真の分位点 (理論値): %.4f\n\n", true_quantile))

# --- シミュレーション実行 ---
# 結果を格納するマトリクス
# 行: シミュレーション回数, 列: type 1 ~ 9
results_matrix <- matrix(NA, nrow = n_sim, ncol = 9)
colnames(results_matrix) <- paste0("Type", 1:9)

for (i in 1:n_sim) {
  # 標準正規分布からランダムサンプルを生成
  sample_data <- rnorm(N, mean = 0, sd = 1)

  # Type 1 から 9 までそれぞれの方法で分位点を計算
  for (t in 1:9) {
    results_matrix[i, t] <- quantile(sample_data, probs = target_prob, type = t)
  }
}

# --- データの整形と要約 ---
# データフレームに変換
df_results <- as.data.frame(results_matrix) %>%
  mutate(Sim_ID = 1:n_sim) %>%
  pivot_longer(cols = starts_with("Type"), names_to = "Type", values_to = "Estimate")

# 各タイプごとの平均値とバイアス（真の値とのズレ）を計算
summary_stats <- df_results %>%
  group_by(Type) %>%
  summarise(
    Mean_Est = mean(Estimate),
    Bias = mean(Estimate) - true_quantile,
    SD = sd(Estimate),
    MSE = mean((Estimate - true_quantile)^2)
  )

print(summary_stats)

サンプルサイズ: 20
ターゲット確率: 0.95
真の分位点 (理論値): 1.6449

# A tibble: 9 × 5
  Type  Mean_Est      Bias    SD   MSE
  <chr>    <dbl>     <dbl> <dbl> <dbl>
1 Type1     1.42 -0.227    0.413 0.222
2 Type2     1.64  0.000123 0.428 0.183
3 Type3     1.42 -0.227    0.413 0.222
4 Type4     1.42 -0.227    0.413 0.222
5 Type5     1.64  0.000123 0.428 0.183
6 Type6     1.85  0.205    0.517 0.309
7 Type7     1.44 -0.204    0.410 0.209
8 Type8     1.71  0.0683   0.451 0.208
9 Type9     1.70  0.0513   0.445 0.200

シミュレーション結果から、「サンプルサイズが小さい（\(N=20\)）場合、分位点の定義（type）によって推定値が異なる」 ことを確認できます。

真の95%分位点は 約 1.645 です。この値を基準に、各タイプの結果を分類して確認します。

# 被積分関数
integrand <- function(x, n) {
  x * n * dnorm(x) * (pnorm(x))^(n - 1)
}

# 積分実行 (-Inf から Inf まで)
expected_value <- integrate(integrand, lower = -Inf, upper = Inf, n = 20)

cat(sprintf("サンプルサイズ20の最大値の理論的期待値: %.4f\n", expected_value$value))

サンプルサイズ20の最大値の理論的期待値: 1.8675

Biasが小さい

• 該当: Type 2, 5, 8, 9
• 結果:
  • Type 2, 5: 平均 1.64。バイアスがほぼ 0 です。
  • Type 8, 9: 平均 1.70 ~ 1.71。わずかにプラスですが、Type 7よりは真の値に近いです。
• 理由:
  • Type 2, 5: 今回の \(N=20, p=0.95\) という設定において、計算上のインデックスがちょうど「19番目の値」と「20番目の値」の中間付近に来るため、両者を平均する形になり、結果として真の値（1.645）に近くなりました（条件によってはズレることもあります）。
  • Type 8, 9: これらは「正規分布に対して不偏（Unbiased）になる」ように設計された定義です。Type 7（デフォルト）よりも裾の方を少し広めに見積もるため、今回のケースではデフォルトよりも良い推定を行っています。

# --- 可視化 ---
# バイオリンプロットと箱ひげ図で分布を比較
p1 <- ggplot(df_results, aes(x = Type, y = Estimate, fill = Type)) +
  # 真の値のライン
  geom_hline(yintercept = true_quantile, color = "red", linetype = "dashed", linewidth = 1) +
  # 分布の表示
  geom_violin(alpha = 0.5, trim = FALSE) +
  geom_boxplot(width = 0.2, outlier.shape = 1, outlier.alpha = 0.3) +
  # 平均値の点を追加
  stat_summary(fun = mean, geom = "point", shape = 18, size = 3, color = "black") +
  labs(
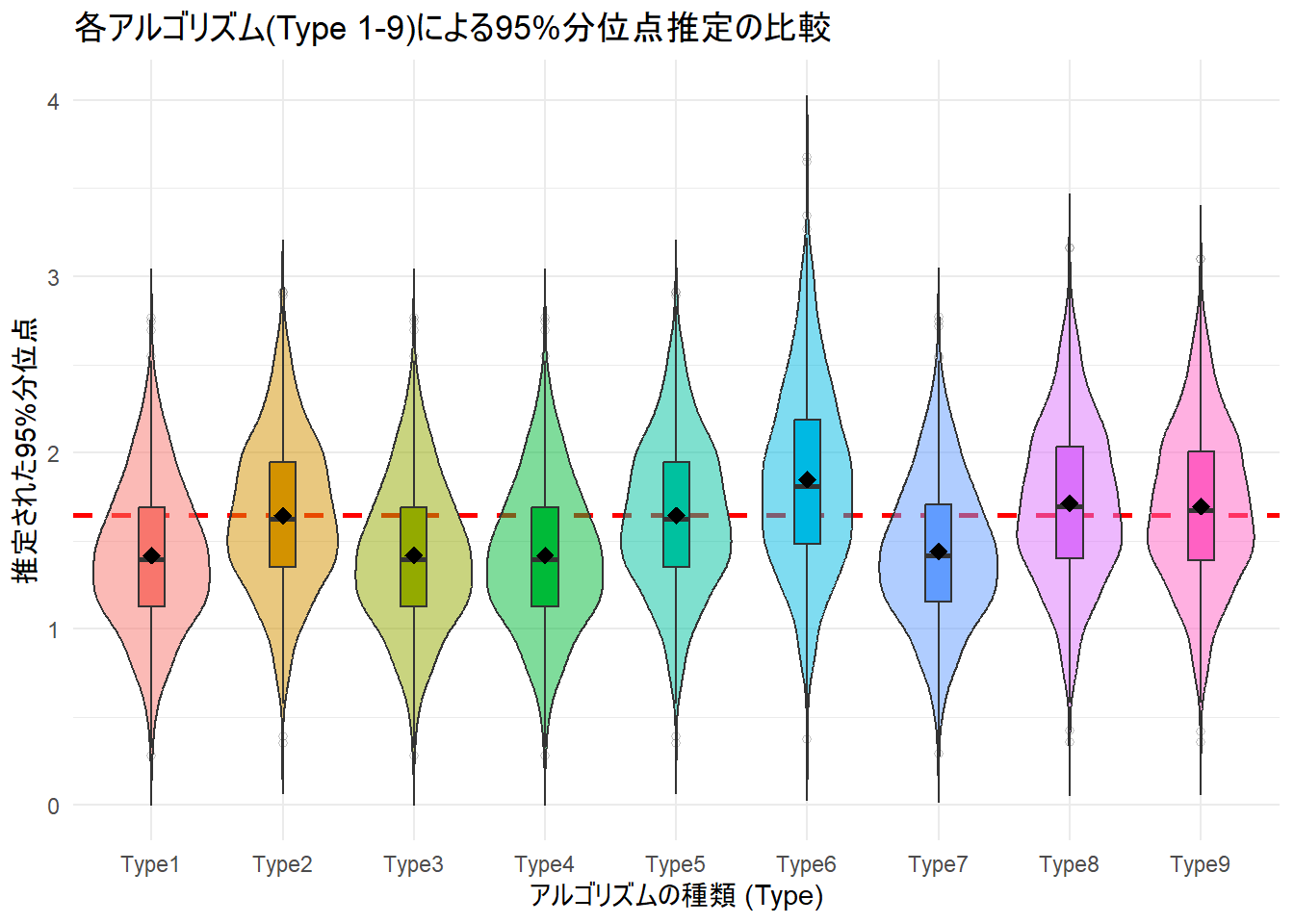
    title = "各アルゴリズム(Type 1-9)による95%分位点推定の比較",
    x = "アルゴリズムの種類 (Type)",
    y = "推定された95%分位点"
  ) +
  theme_minimal() +
  theme(legend.position = "none")

print(p1)

# 平均的なバイアスの可視化
p2 <- ggplot(summary_stats, aes(x = Type, y = Bias, fill = abs(Bias))) +
  geom_bar(stat = "identity") +
  geom_hline(yintercept = 0, color = "black") +
  labs(
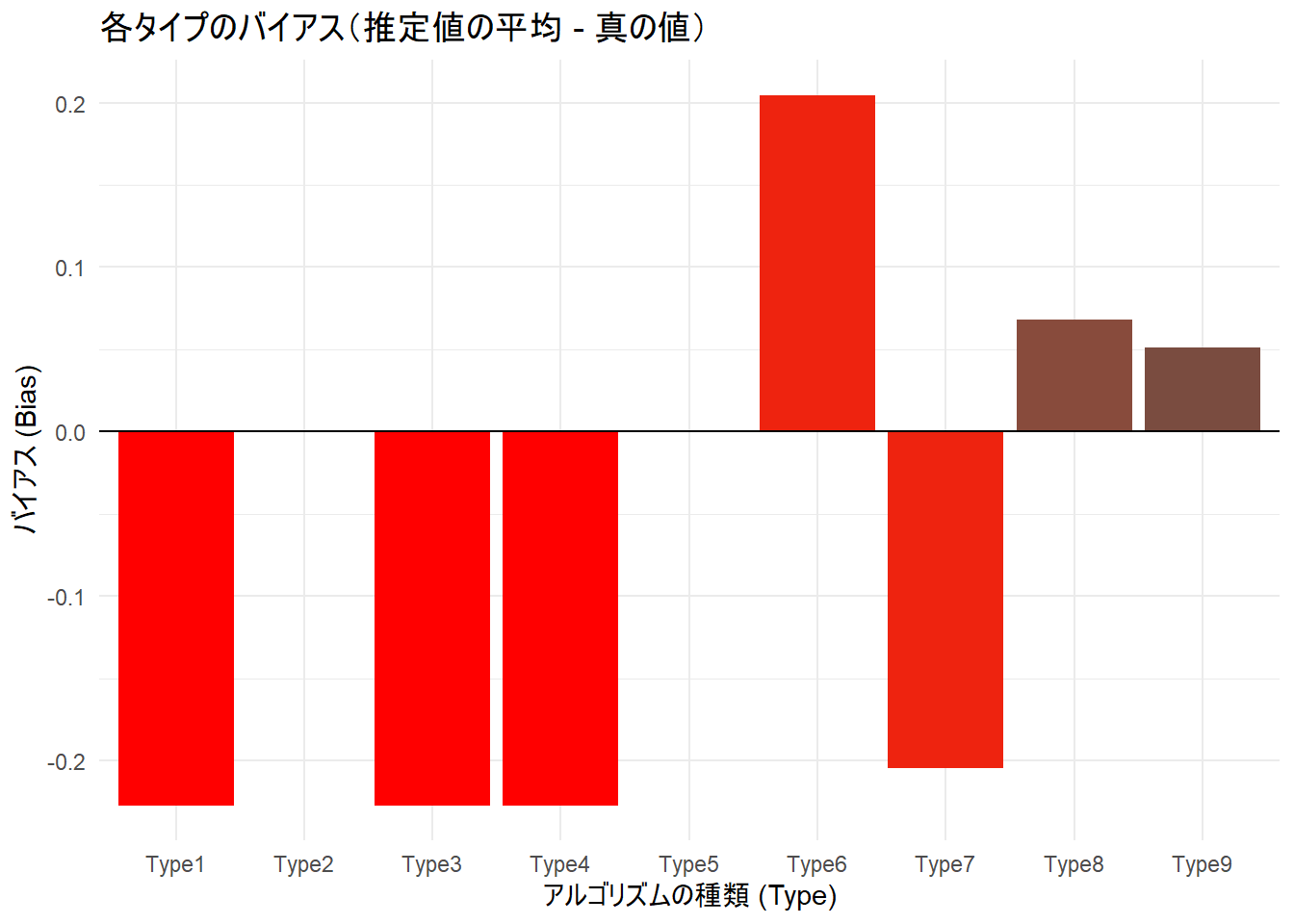
    title = "各タイプのバイアス（推定値の平均 - 真の値）",
    x = "アルゴリズムの種類 (Type)",
    y = "バイアス (Bias)"
  ) +
  scale_fill_gradient(low = "grey30", high = "red") +
  theme_minimal() +
  theme(legend.position = "none")

print(p2)

Figure 1 の赤点線は真の値 (1.645)を示しています。Typeによって推定値の中心位置が異なることを確認できます。

Figure 2 では、0に近いほど偏りがないことを意味しますが、Typeによって過大評価・過小評価の傾向が異なることを確認できます。

以上です。