RStan を利用して 時系列データの欠損値推定 を試みます。
1. 必要なパッケージの準備
シミュレーションに必要なRパッケージを読み込みます。
# RStanの読み込み
library(rstan)
stan_output <- "D:/stan_output"
# Stanの並列計算設定
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
# rstan のバージョン確認
cat("--- パッケージ rstan のバージョン確認 ---\n")
sapply(X = c("rstan"), packageVersion)--- パッケージ rstan のバージョン確認 ---
$rstan
[1] 2 32 72. 時系列サンプルデータの作成
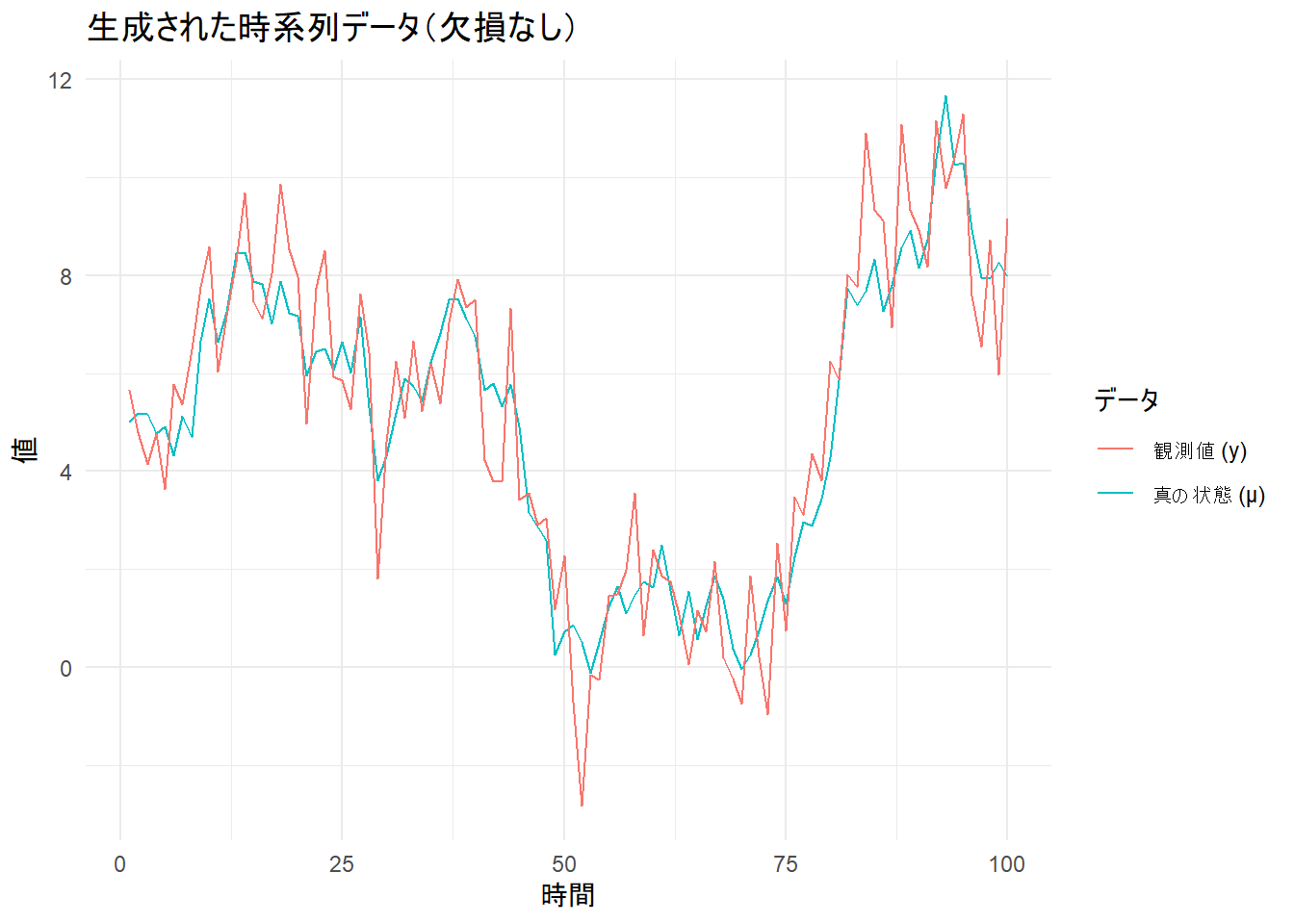
ここでは、時系列モデルである「ローカルレベルモデル」を用いて、欠損のないサンプルデータを作成します。このモデルは、システムの真の状態(μ)がランダムウォークに従い、観測値(y)がその真の状態にノイズ(観測誤差)を加えたものとして生成される、という考え方に基づいています。
- 状態方程式:
μ[t] = μ[t-1] + w[t], ここでw[t] ~ Normal(0, σ_w^2) - 観測方程式:
y[t] = μ[t] + v[t], ここでv[t] ~ Normal(0, σ_v^2)
# シミュレーションのための設定
seed <- 20250630
set.seed(seed)
T <- 100 # 時系列の長さ
mu1 <- 5 # 初期状態
sigma_w <- 0.8 # システムノイズの標準偏差
sigma_v <- 1.2 # 観測ノイズの標準偏差
# 真の状態(mu)と観測値(y_true)を格納するベクトルを準備
mu <- numeric(T)
y_true <- numeric(T)
# データを生成
mu[1] <- mu1
for (t in 2:T) {
mu[t] <- rnorm(1, mean = mu[t - 1], sd = sigma_w)
}
y_true <- rnorm(T, mean = mu, sd = sigma_v)
# データフレームにまとめる
original_data <- data.frame(
time = 1:T,
mu_true = mu,
y_true = y_true
)
# 生成したデータを確認
library(ggplot2)
ggplot(original_data, aes(x = time)) +
geom_line(aes(y = mu_true, color = "真の状態 (μ)")) +
geom_line(aes(y = y_true, color = "観測値 (y)")) +
labs(
title = "生成された時系列データ(欠損なし)",
x = "時間", y = "値", color = "データ"
) +
theme_minimal()3. 欠損値の作成
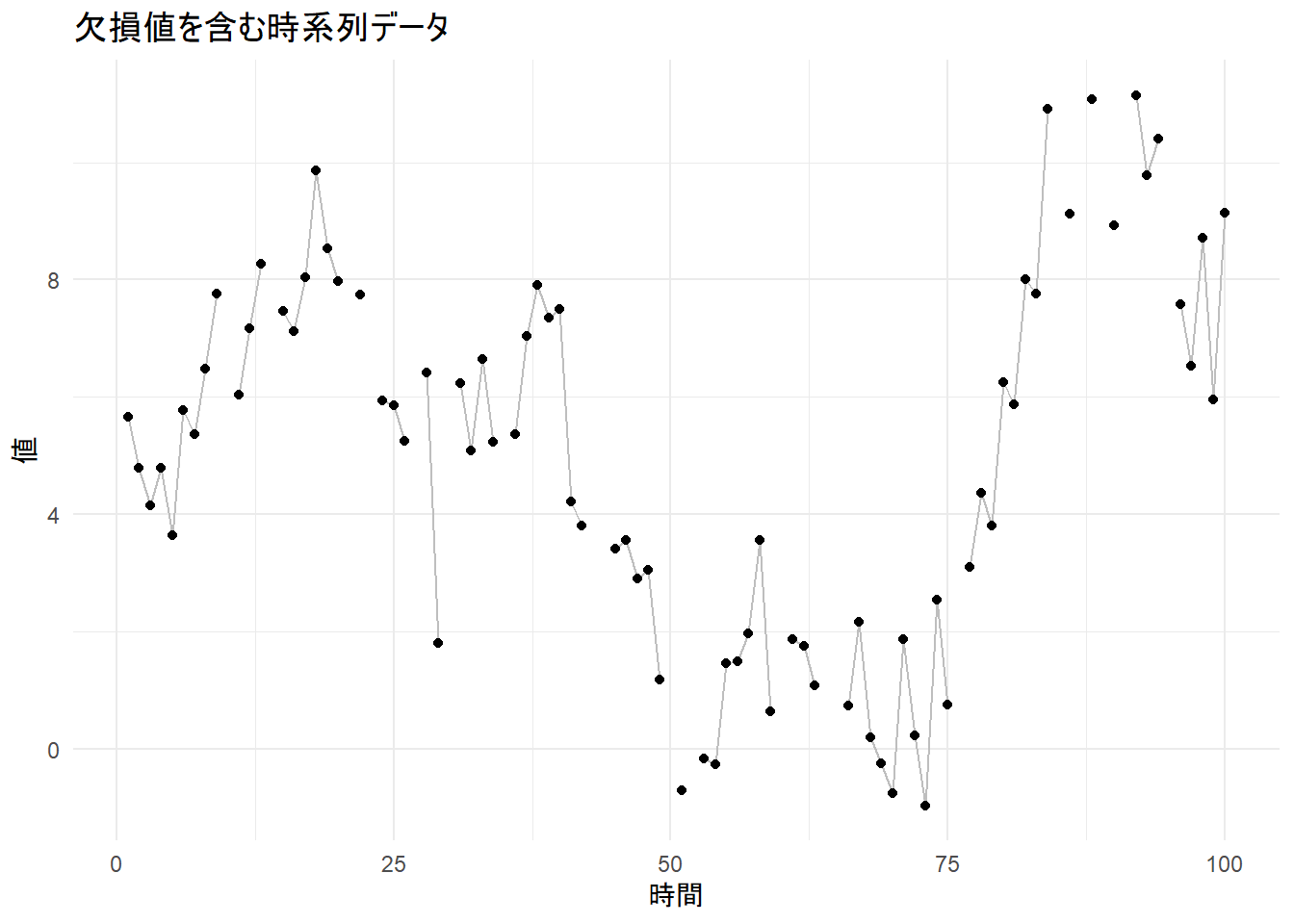
作成した y_true からランダムに20点を取り除き、欠損値 (NA) を持つ観測データ y_obs を作成します。
set.seed(seed)
# 欠損させるデータ点の数
n_missing <- 20
# 欠損させる位置をランダムに選ぶ
missing_indices <- sample(1:T, size = n_missing)
# 欠損値を含むデータを作成
y_obs <- y_true
y_obs[missing_indices] <- NA
# 最終的なデータフレームを作成
library(dplyr)
sim_data <- original_data %>%
mutate(y_obs = y_obs)
# 欠損データを確認
ggplot(sim_data, aes(x = time, y = y_obs)) +
geom_line(color = "gray") +
geom_point(color = "black") +
labs(title = "欠損値を含む時系列データ", x = "時間", y = "値") +
theme_minimal()4. Stanモデルの定義
欠損値を推定するためのStanモデルを記述します。これは、データを生成したローカルレベルモデルと同じ構造です。
-
dataブロック: RからStanに渡すデータを定義します。 -
parametersブロック: MCMCで推定するパラメータを定義します。欠損値y_misもここでパラメータとして扱います。 -
modelブロック: パラメータの事前分布と、データが生成される尤度(モデル)を定義します。 -
generated quantitiesブロック: MCMCサンプリング後に、推定されたパラメータから目的の値を生成します。ここでは、観測値と推定した欠損値を結合して、完全な時系列データy_imputedを作成します。
推定のプロセスは以下のようになります。
- MCMCサンプラーが、観測データ
y_obsを使って、最も確からしい真の状態muの軌道と、ノイズの大きさ(sigma_w,sigma_v)を推定します。 - 同時に、欠損している時点
t_misにおける真の状態mu[t_mis]も推定されます。 - サンプラーは、その
mu[t_mis]を中心とした正規分布normal(mu[t_mis], sigma_v)から、欠損観測値y_misをサンプリングします。 - このプロセスが繰り返されることで、
muとy_misの両方の事後分布が得られます。
model_code <- "
data {
int<lower=0> T; // 時系列の長さ
int<lower=0> N_obs; // 観測されたデータ点の数
int<lower=0> N_mis; // 欠損したデータ点の数
vector[N_obs] y_obs; // 観測されたデータ
int<lower=1, upper=T> ii_obs[N_obs]; // 観測されたデータのインデックス
int<lower=1, upper=T> ii_mis[N_mis]; // 欠損したデータのインデックス
}
parameters {
// 非中心化のためのパラメータ
real mu1; // 初期状態 mu[1]
vector[T-1] mu_raw; // 標準正規分布に従うオフセット項
vector[N_mis] y_mis; // 欠損値
real<lower=0> sigma_w; // システムノイズの標準偏差
real<lower=0> sigma_v; // 観測ノイズの標準偏差
}
transformed parameters {
vector[T] mu; // 観測ノイズを含まない潜在状態をここで構築
mu[1] = mu1;
for (t in 2:T) {
// mu_raw を使って mu[t] を計算
mu[t] = mu[t - 1] + mu_raw[t - 1] * sigma_w;
}
}
model {
// 事前分布
sigma_w ~ cauchy(0, 2.5);
sigma_v ~ cauchy(0, 2.5);
mu1 ~ normal(0, 10); // 初期状態の事前分布
// 非中心化されたパラメータの事前分布
mu_raw ~ std_normal(); // mu_raw ~ normal(0, 1) と同じ意味
// 観測方程式(尤度)
y_obs ~ normal(mu[ii_obs], sigma_v);
y_mis ~ normal(mu[ii_mis], sigma_v);
}
generated quantities {
vector[T] y_imputed; // 推定された欠損値を含む完全な時系列
y_imputed[ii_obs] = y_obs;
y_imputed[ii_mis] = y_mis;
}
"5. RStanによるMCMC推定の実行
Stanモデルに渡すためのデータをリスト形式で準備し、stan() 関数でMCMCサンプリングを実行します。
# Stanに渡すためのデータリストを作成
stan_data <- list(
T = T,
N_obs = T - n_missing,
N_mis = n_missing,
y_obs = y_obs[!is.na(y_obs)],
ii_obs = which(!is.na(y_obs)),
ii_mis = which(is.na(y_obs))
)
# Stanモデルのコンパイルと実行
fit <- stan(
model_code = model_code,
data = stan_data,
iter = 2000,
warmup = 1000,
chains = 4,
seed = seed
)
# stanfit オブジェクトの保存
setwd(stan_output)
saveRDS(object = fit, file = "stan_fit.rds")6. 結果の抽出と可視化
要約統計量の確認
MCMCの実行結果から、推定された潜在状態 mu と、補完された時系列 y_imputed の要約統計量(平均、95%信用区間など)を抽出します。
# stanfit オブジェクトの読み込み
setwd(stan_output)
fit <- readRDS("stan_fit.rds")
# MCMCサンプルから要約統計量を抽出
summary_fit <- summary(fit,
pars = c("mu", "y_imputed", "sigma_w", "sigma_v"),
probs = c(0.025, 0.5, 0.975)
)$summary
# 結果をデータフレームに整形
results_df <- sim_data %>%
mutate(
mu_mean = summary_fit[grep("mu\\[", rownames(summary_fit)), "mean"],
mu_lower = summary_fit[grep("mu\\[", rownames(summary_fit)), "2.5%"],
mu_upper = summary_fit[grep("mu\\[", rownames(summary_fit)), "97.5%"],
y_imputed_mean = summary_fit[grep("y_imputed\\[", rownames(summary_fit)), "mean"],
y_imputed_lower = summary_fit[grep("y_imputed\\[", rownames(summary_fit)), "2.5%"],
y_imputed_upper = summary_fit[grep("y_imputed\\[", rownames(summary_fit)), "97.5%"],
is_missing = is.na(y_obs) # 欠損点かどうかを判別する列
)
cat("--- 推定されたパラメータの確認 ---\n")
print(summary_fit[c("sigma_w", "sigma_v"), ])--- 推定されたパラメータの確認 ---
mean se_mean sd 2.5% 50% 97.5% n_eff
sigma_w 0.9468056 0.005743116 0.1461394 0.6856029 0.9364131 1.260118 647.4995
sigma_v 0.9270964 0.005794203 0.1362888 0.6624491 0.9253443 1.203040 553.2648
Rhat
sigma_w 1.006331
sigma_v 1.007118stanコードの実行の結果、以下の警告メッセージが出ます。
警告メッセージ:
1: There were 39 divergent transitions after warmup. See

但し、要約統計量を確認しますと、真値 sigma_w=0.8, sigma_v=1.2 はいずれも 95%信用区間 に含まれており(sigma_v はギリギリ)、Rhat は ほぼ 1.0 であるため、本シミュレーションでは先に進みます。
チャートによる結果の可視化
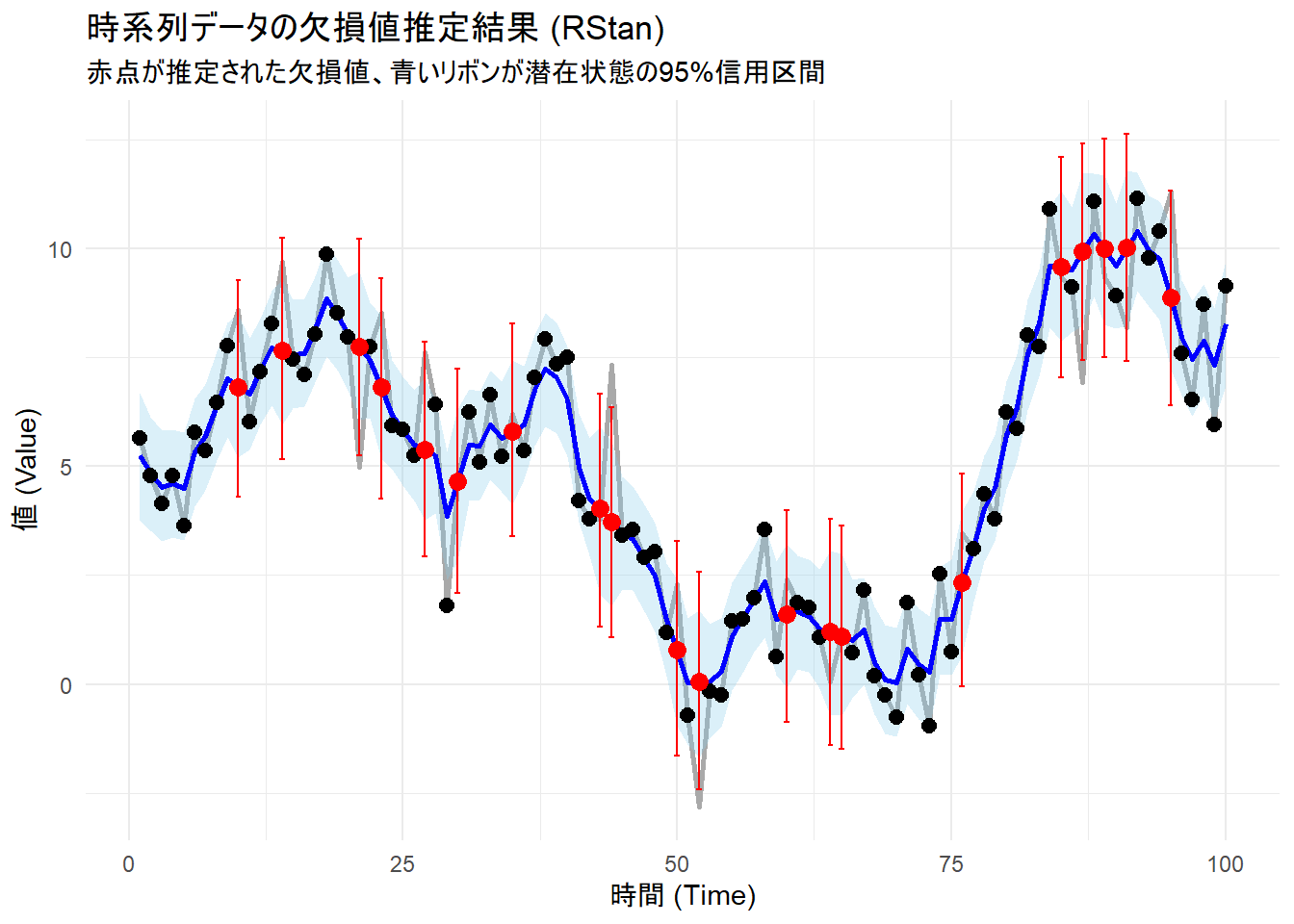
1. 時系列データの欠損値推定結果
# 結果のプロット
ggplot(results_df, aes(x = time)) +
# 1. 観測値のデータ(比較用)
geom_line(aes(y = y_true), color = "darkgray", linewidth = 1) +
# 2. 推定された潜在状態(mu)の95%信用区間
geom_ribbon(aes(ymin = mu_lower, ymax = mu_upper), fill = "skyblue", alpha = 0.3) +
# 3. 推定された潜在状態(mu)の平均値
geom_line(aes(y = mu_mean), color = "blue", linewidth = 1) +
# 4. 観測されたデータ点
geom_point(aes(y = y_obs), color = "black", size = 2.5, na.rm = TRUE) +
# 5. 欠損観測値の推定値(平均値)
geom_point(data = . %>% filter(is_missing), aes(y = y_imputed_mean), color = "red", size = 3) +
# 6. 欠損観測値の推定値の95%信用区間
geom_errorbar(data = . %>% filter(is_missing), aes(ymin = y_imputed_lower, ymax = y_imputed_upper), color = "red", width = 0.5) +
# ラベルとテーマ
labs(
title = "時系列データの欠損値推定結果 (RStan)",
subtitle = "赤点が推定された欠損値、青いリボンが潜在状態の95%信用区間",
x = "時間 (Time)",
y = "値 (Value)"
) +
theme_minimal()- 青い線とリボン: 推定された観測ノイズを含まない潜在状態
μとその不確実性(95%信用区間)を表します。 - 黒い点: 実際に観測された欠損ありのデータ点です。
- 赤い点とエラーバー: 今回の主目的である、推定された欠損観測値とその不確実性(95%信用区間)です。
- 灰色の線: シミュレーションの「答え」である欠損なしの観測値です。
Figure 3 から、「データが観測されている点ではリボンの幅が狭く(不確実性が低い)、欠損している区間ではリボンの幅が広くなっていること(不確実性が高い)」、「推定された欠損観測値の95%信用区間(赤いエラーバー)は、欠損とした実際の観測値(灰色の線)を ほぼカバーしていること」が確認できます。
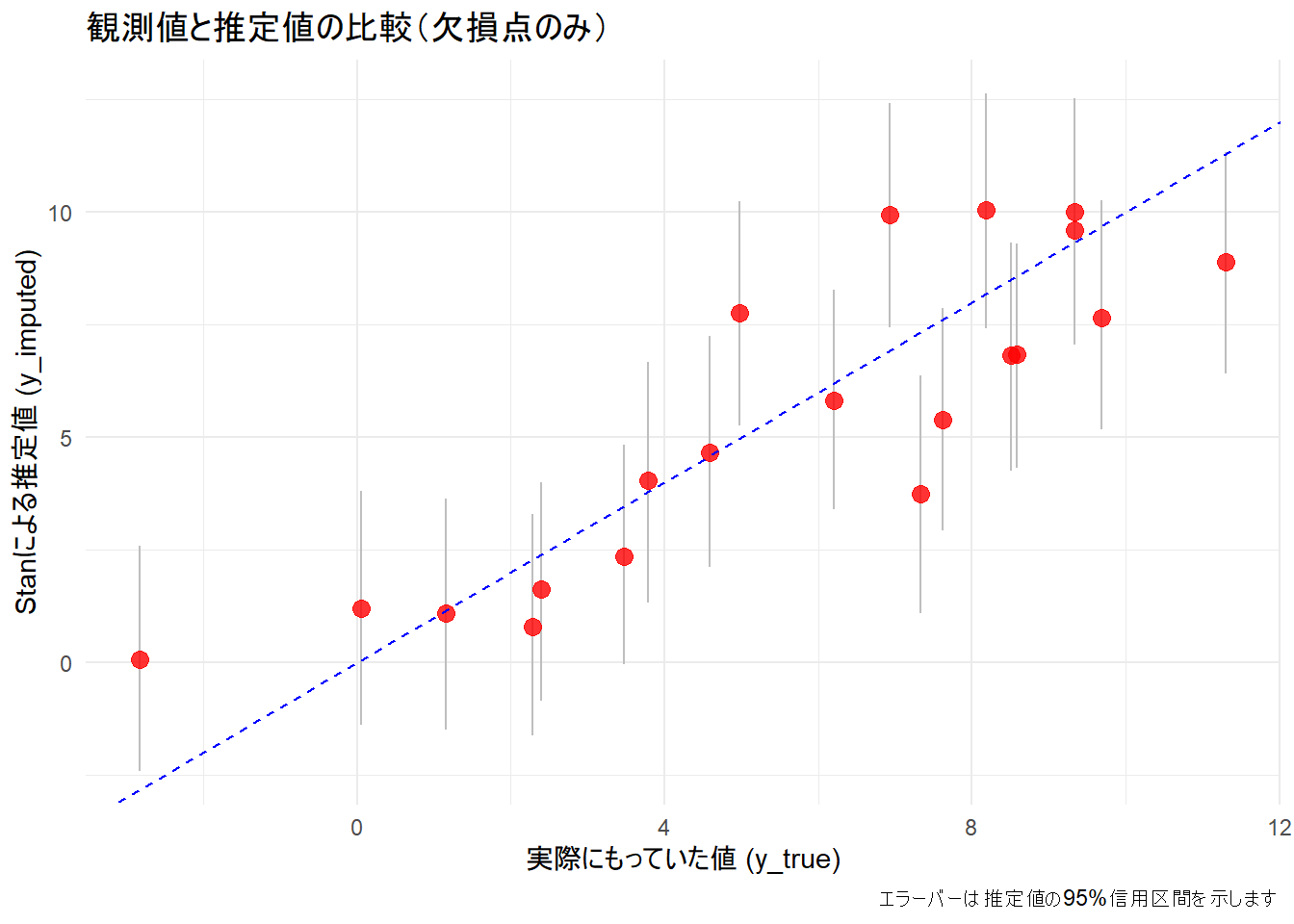
2. 観測値と推定値の比較(欠損点のみ)
# 欠損していた箇所のデータのみを抽出
missing_comparison_df <- results_df %>%
filter(is_missing == TRUE) %>% # is_missingがTRUEの行(欠損点)のみをフィルタリング
select(
time,
y_true, # 実際の観測値(欠損前の値)
y_imputed_mean, # 推定された欠損観測値(事後平均値)
y_imputed_lower, # 推定値の95%信用区間の下限
y_imputed_upper # 推定値の95%信用区間の上限
)
# 散布図を作成して比較
ggplot(missing_comparison_df, aes(x = y_true, y = y_imputed_mean)) +
# 推定値の95%信用区間をエラーバーで表示
geom_errorbar(aes(ymin = y_imputed_lower, ymax = y_imputed_upper), color = "gray", width = 0) +
# 推定値の平均を点でプロット
geom_point(color = "red", size = 3, alpha = 0.8) +
# 理想的な直線 (y = x) を破線で追加
geom_abline(intercept = 0, slope = 1, linetype = "dashed", color = "blue") +
# 軸の範囲を調整して見やすくする
# coord_fixed(
# xlim = range(c(missing_comparison_df$y_true, missing_comparison_df$y_imputed_lower)),
# ylim = range(c(missing_comparison_df$y_true, missing_comparison_df$y_imputed_upper))
# ) +
labs(
title = "観測値と推定値の比較(欠損点のみ)",
x = "実際にもっていた値 (y_true)",
y = "Stanによる推定値 (y_imputed)",
caption = "エラーバーは推定値の95%信用区間を示します"
) +
theme_minimal()- 赤い点 が 青い破線(y=xの線)に近いほど、推定値の平均が実際の観測値に近いことを意味します。
- 縦方向のグレーの線(エラーバー) は、各点の推定の不確実性(95%信用区間)を表します。
Figure 4 から、「ほとんどのグレーの線が青い破線と交差していますので、推定された欠損値の事後分布が実際の観測値を ほぼ 捉えられている」ことが確認できます。
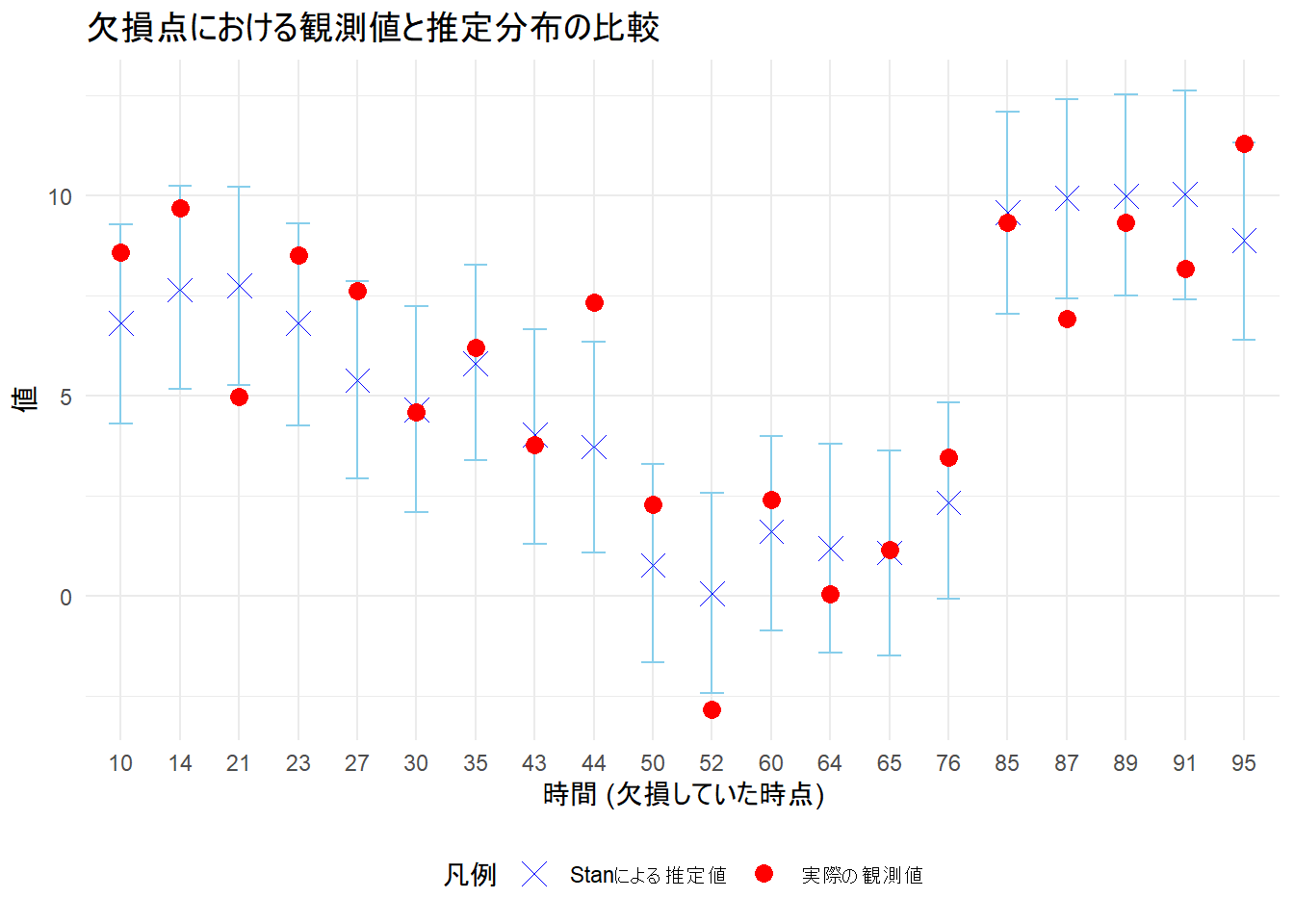
3. 欠損点における観測値と推定分布の比較
# 欠損点のみのデータで、時系列順にプロット
ggplot(missing_comparison_df, aes(x = factor(time))) +
# 推定値の95%信用区間
geom_errorbar(aes(ymin = y_imputed_lower, ymax = y_imputed_upper), width = 0.4, color = "skyblue") +
# 推定値の平均値
geom_point(aes(y = y_imputed_mean), shape = 4, size = 4, color = "blue") +
# 実際の値(真値)
geom_point(aes(y = y_true), shape = 16, size = 3, color = "red") +
# 凡例のためのダミーaes
geom_point(aes(y = y_imputed_mean, color = "Stanによる推定値"), alpha = 0) +
geom_point(aes(y = y_true, color = "実際の観測値"), alpha = 0) +
scale_color_manual(
name = "凡例",
values = c("Stanによる推定値" = "blue", "実際の観測値" = "red"),
guide = guide_legend(
override.aes = list(
shape = c(4, 16),
size = c(4, 3),
alpha = c(1, 1),
color = c("blue", "red")
)
)
) +
labs(
title = "欠損点における観測値と推定分布の比較",
x = "時間 (欠損していた時点)",
y = "値"
) +
theme_minimal() +
theme(legend.position = "bottom")- 赤い点が実際の観測値(欠損値)です。
- 青いバツ印がStanによる推定値の平均です。
- 水色のエラーバーが推定値の95%信用区間です。
Figure 5 から、「ほとんど全ての赤い点(観測値)が、水色のエラーバー(95%信用区間)の範囲内に収まっている」ことが確認できます。
以上です。