RStan を利用して 階層ベイズモデル を試みます。
1. シナリオ:学習塾チェーンの模擬試験分析
ストーリー設定
あなたは架空の大手学習塾チェーン「ベイズゼミナール」のデータサイエンティストです。ベイズゼミナールは全国に10校の校舎を展開しています。先日、全校舎で一斉に同じ内容の模擬試験を実施しました。
各校舎には、立地や担当講師の指導方針によって、生徒の学力に「校舎ごとのクセ」があると考えられます。例えば、A校は理系に強い、B校は文系に強いなどです。しかし、それらの校舎は全て「ベイズゼミナール」という一つのブランドの下にあり、共通のカリキュラムや教材を使っているため、完全に無関係なわけではありません。
あなたの仕事は、今回の模擬試験の点数データを分析し、以下の点を明らかにすることです。
- 各校舎の「真の平均学力」はどのくらいか?
- 校舎間の学力には、どの程度のばらつきがあるのか?
- ベイズゼミナール全体としての平均的な学力はどのレベルか?
単純に校舎ごとの平均点を計算するだけでは、生徒数が少ない校舎の成績が偶然良い(または悪い)結果だった場合に、その校舎の実力を過大(または過小)評価してしまう危険性があります。そこで、全校舎の情報をうまく活用し、より妥当な推定を行うために階層ベイズモデルを用いることにしました。
2. シミュレーションとモデリングの実装
ステップ1:必要なパッケージの読み込み
# RStanの読み込み
library(rstan)
stan_output <- "D:/stan_output"
# Stanの並列計算設定
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
# rstan のバージョン確認
cat("--- パッケージ rstan のバージョン確認 ---\n")
sapply(X = c("rstan"), packageVersion)--- パッケージ rstan のバージョン確認 ---
$rstan
[1] 2 32 7ステップ2:シミュレーションデータの生成
シナリオに基づいて、模擬試験の点数データを生成します。
# シミュレーションのパラメータ設定
J <- 10 # 校舎の数
N_j <- 20 # 各校舎の生徒数
N <- J * N_j # 全生徒数
# 真のパラメータ
mu_true <- 60 # 全校舎の平均学力の平均(グランド平均)
sigma_g_true <- 10 # 校舎間の学力レベルのばらつき
sigma_s_true <- 15 # 生徒間の成績のばらつき(校舎内SD)
seed <- 20250701
set.seed(seed)
# 1. 各校舎の真の平均学力(theta)を生成
theta_true <- rnorm(n = J, mean = mu_true, sd = sigma_g_true)
# 2. 各生徒のデータを生成
school_id <- rep(1:J, each = N_j)
score <- numeric(N)
for (i in 1:N) {
score[i] <- rnorm(n = 1, mean = theta_true[school_id[i]], sd = sigma_s_true)
}
# データフレームにまとめる
sim_data <- data.frame(
student_id = 1:N,
school_id = factor(school_id),
score = score
)
cat("--- 生成したデータの一部を確認 ---\n")
head(sim_data)
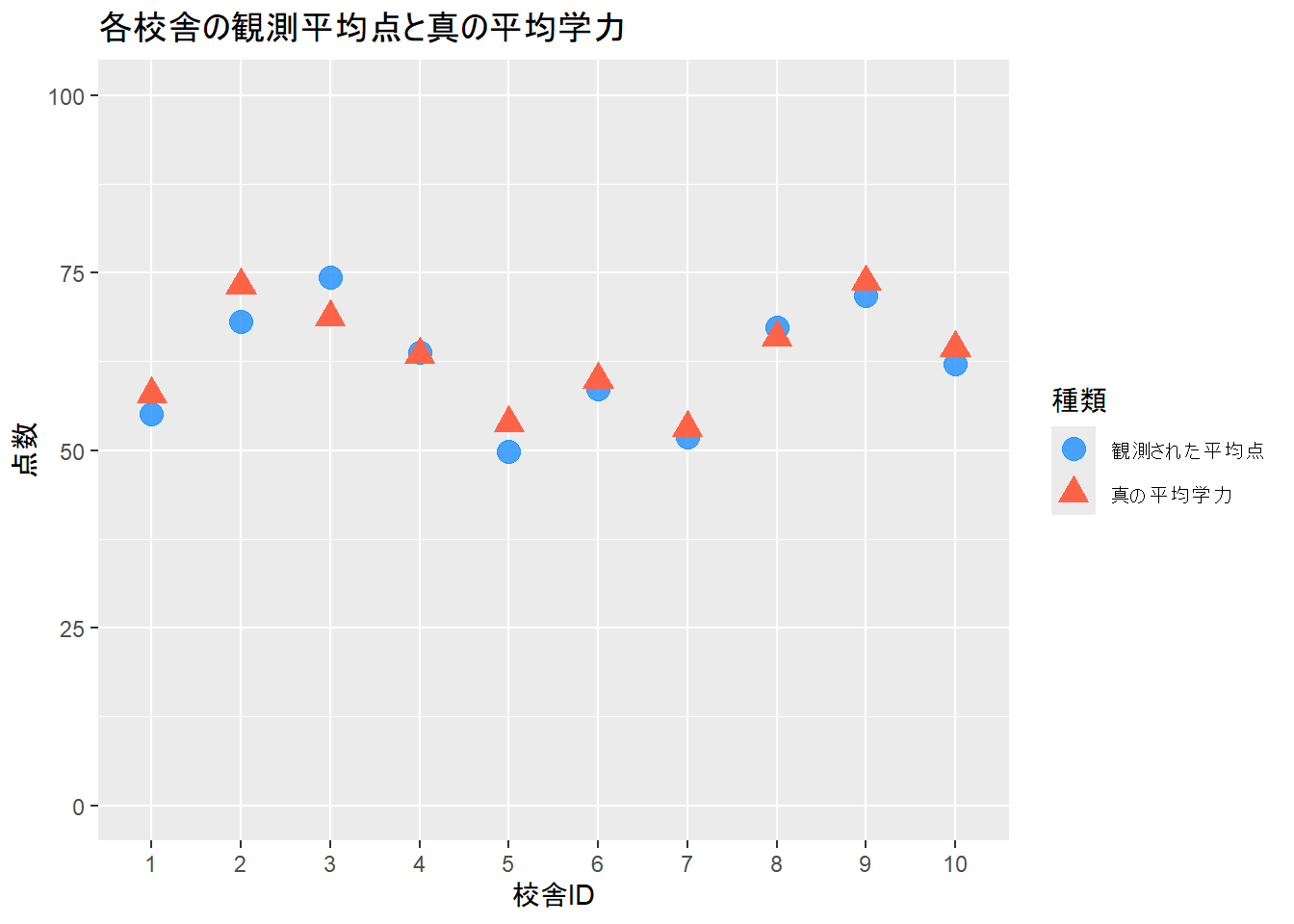
# 校舎ごとの単純な平均点と真の値をプロット
library(ggplot2)
library(dplyr)
sim_data %>%
group_by(school_id) %>%
summarise(raw_mean_score = mean(score)) %>%
mutate(true_theta = theta_true) %>%
ggplot(aes(x = school_id)) +
geom_point(aes(y = raw_mean_score, colour = "観測された平均点"), size = 4, alpha = 0.8) +
geom_point(aes(y = true_theta, colour = "真の平均学力"), size = 4, shape = 17) +
labs(
title = "各校舎の観測平均点と真の平均学力",
x = "校舎ID", y = "点数", colour = "種類"
) +
scale_color_manual(values = c("観測された平均点" = "dodgerblue", "真の平均学力" = "tomato")) +
ylim(0, 100)--- 生成したデータの一部を確認 ---
student_id school_id score
1 1 1 84.01964
2 2 1 67.99745
3 3 1 37.40326
4 4 1 55.44087
5 5 1 55.20703
6 6 1 66.05562Figure 1 から、観測された平均点は、真の平均学力からずれていることがわかります。特に生徒数が少ない場合、このずれは大きくなります。
ステップ3:Stanモデルの定義(非中心化パラメータ化)
階層ベイズモデルをStanで記述します。ここではサンプリング効率を向上させるため、非中心化パラメータ化(Non-centered Parameterization)を用います。
theta を直接パラメータとして推定する代わりに、標準正規分布に従う theta_raw を推定し、transformed parameters ブロックで theta を計算します。
model_code <- "
data {
int<lower=0> N; // 全生徒数
int<lower=0> J; // 校舎数
array[N] int<lower=1, upper=J> school_id; // 各生徒の校舎ID
vector[N] score; // 各生徒の点数
}
parameters {
real mu; // 全体の平均(グランド平均)
real<lower=0> sigma_g; // 校舎間SD
real<lower=0> sigma_s; // 校舎内SD(生徒間SD)
vector[J] theta_raw; // 非中心化パラメータ (標準正規分布に従う)
}
transformed parameters {
vector[J] theta; // 各校舎の平均学力
// theta_rawからthetaを計算
// これにより、mu, sigma_g, theta間の事後相関が弱まり、サンプリングが効率化される
theta = mu + sigma_g * theta_raw;
}
model {
// 事前分布
mu ~ normal(60, 20); // 全体の平均は60点くらいだろう、という弱い情報
sigma_g ~ student_t(3, 0, 10); // 正の値のみをとる頑健な事前分布
sigma_s ~ student_t(3, 0, 10); // 同上
theta_raw ~ std_normal(); // <=> theta_raw ~ normal(0, 1);
// 尤度
// 各生徒のscoreは、所属する校舎の平均theta[school_id]に従う
score ~ normal(theta[school_id], sigma_s);
}
"ステップ4:RStanによるMCMCサンプリングの実行
作成したモデルとデータを使って、ベイズ推定を実行します。
# Stanに渡すためのデータリストを作成
stan_data <- list(
N = N,
J = J,
school_id = as.integer(sim_data$school_id),
score = sim_data$score
)
# MCMCの実行
fit <- stan(
model_code = model_code,
data = stan_data,
iter = 2000,
warmup = 1000,
chains = 4,
seed = seed
)
# stanfit オブジェクトの保存
setwd(stan_output)
saveRDS(object = fit, file = "stan_fit.rds")ステップ5:結果の確認と可視化
1. パラメータの推定結果の要約
# stanfit オブジェクトの読み込み
setwd(stan_output)
fit <- readRDS("stan_fit.rds")
# 結果の要約を表示
cat("--- 結果の要約 ---\n")
summary(fit,
pars = c("mu", "sigma_g", "sigma_s"),
probs = c(0.025, 0.5, 0.975)
)$summary--- 結果の要約 ---
mean se_mean sd 2.5% 50% 97.5% n_eff
mu 62.286887 0.09437335 2.8976756 56.386348 62.254775 68.35408 942.7591
sigma_g 8.353483 0.07415645 2.5089084 4.661869 7.953127 14.53668 1144.6475
sigma_s 15.276016 0.01304754 0.7788874 13.877565 15.247096 16.91567 3563.6245
Rhat
mu 1.000725
sigma_g 1.003006
sigma_s 0.999947stanコード実行の結果、警告メッセージ は出されず、シミュレーションで設定した真の値(mu_true=60, sigma_g_true=10, sigma_s_true=15)は、それぞれの 95%信用区間 に含まれており、Rhat はいずれも 1.0 に近いため、モデルはうまくデータを捉えられていると判断します。
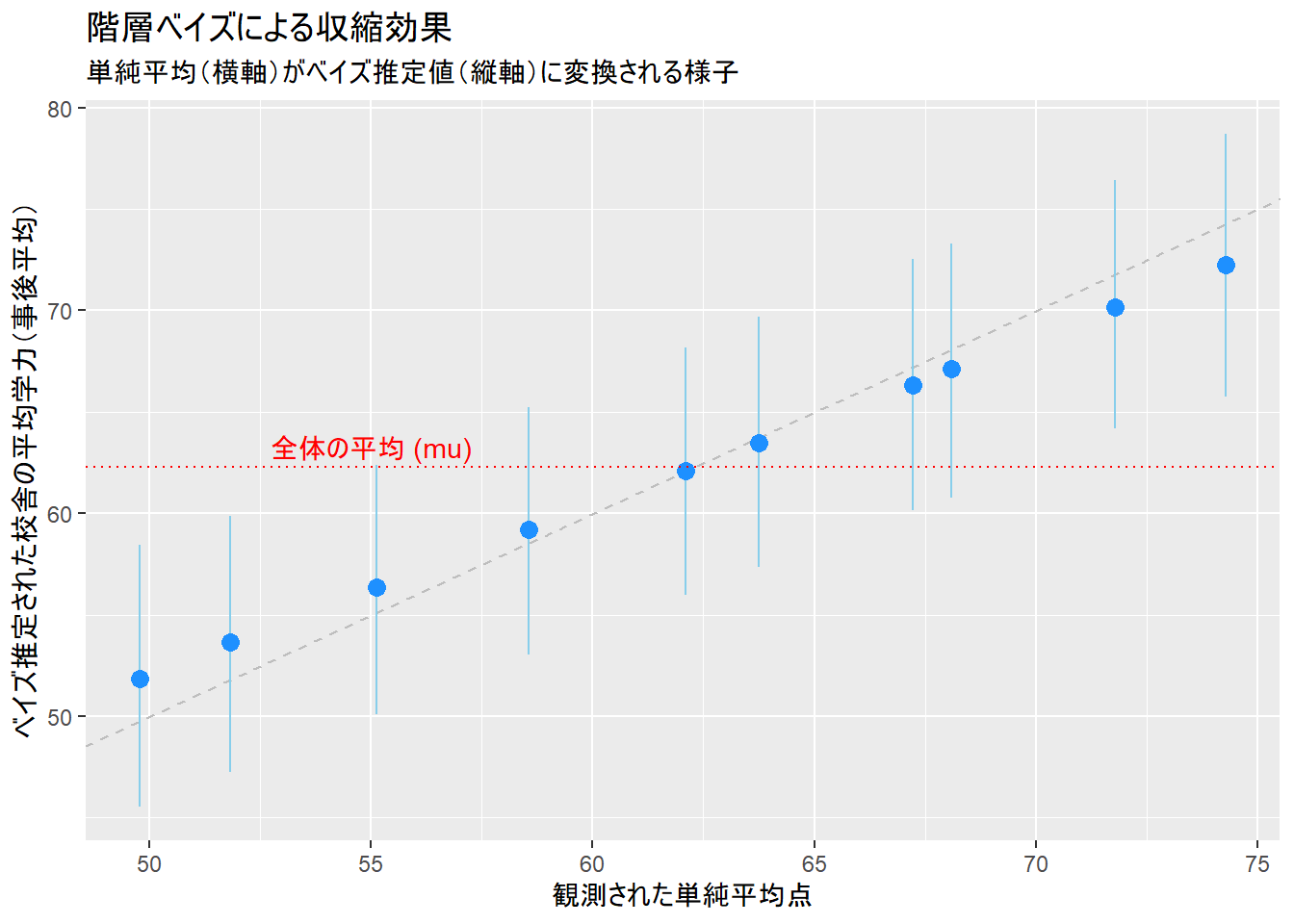
2. 収縮(Shrinkage)効果の可視化
階層ベイズモデルの「収縮」をグラフで確認します。
# MCMCサンプルからthetaの推定値を取得
theta_est <- rstan::extract(fit, pars = "theta")$theta
# thetaの事後平均と95%信用区間を計算
theta_summary <- data.frame(
school_id = 1:J,
mean = apply(theta_est, 2, mean),
q2.5 = apply(theta_est, 2, quantile, probs = 0.025),
q97.5 = apply(theta_est, 2, quantile, probs = 0.975)
)
# 観測された単純平均と真の値を結合
plot_data <- sim_data %>%
group_by(school_id) %>%
summarise(raw_mean = mean(score)) %>%
mutate(school_id = as.integer(school_id)) %>%
left_join(theta_summary, by = "school_id") %>%
mutate(true_theta = theta_true)
# 収縮プロット
ggplot(plot_data, aes(x = raw_mean, y = mean)) +
geom_abline(slope = 1, intercept = 0, linetype = "dashed", color = "gray") +
geom_errorbar(aes(ymin = q2.5, ymax = q97.5), width = 0, color = "skyblue") +
geom_point(color = "dodgerblue", size = 3) +
geom_hline(yintercept = mean(rstan::extract(fit, pars = "mu")$mu), linetype = "dotted", color = "red") +
annotate("text",
x = 55, y = mean(rstan::extract(fit, pars = "mu")$mu) + 1,
label = "全体の平均 (mu)", color = "red"
) +
labs(
title = "階層ベイズによる収縮効果",
subtitle = "単純平均(横軸)がベイズ推定値(縦軸)に変換される様子",
x = "観測された単純平均点",
y = "ベイズ推定された校舎の平均学力(事後平均)"
)Figure 2 の青い点は、縦軸がベイズ推定値、横軸が単純な観測平均値です。観測平均が高かった校舎の推定値は下方修正され、低かった校舎の推定値は上方修正されていることが確認できます。
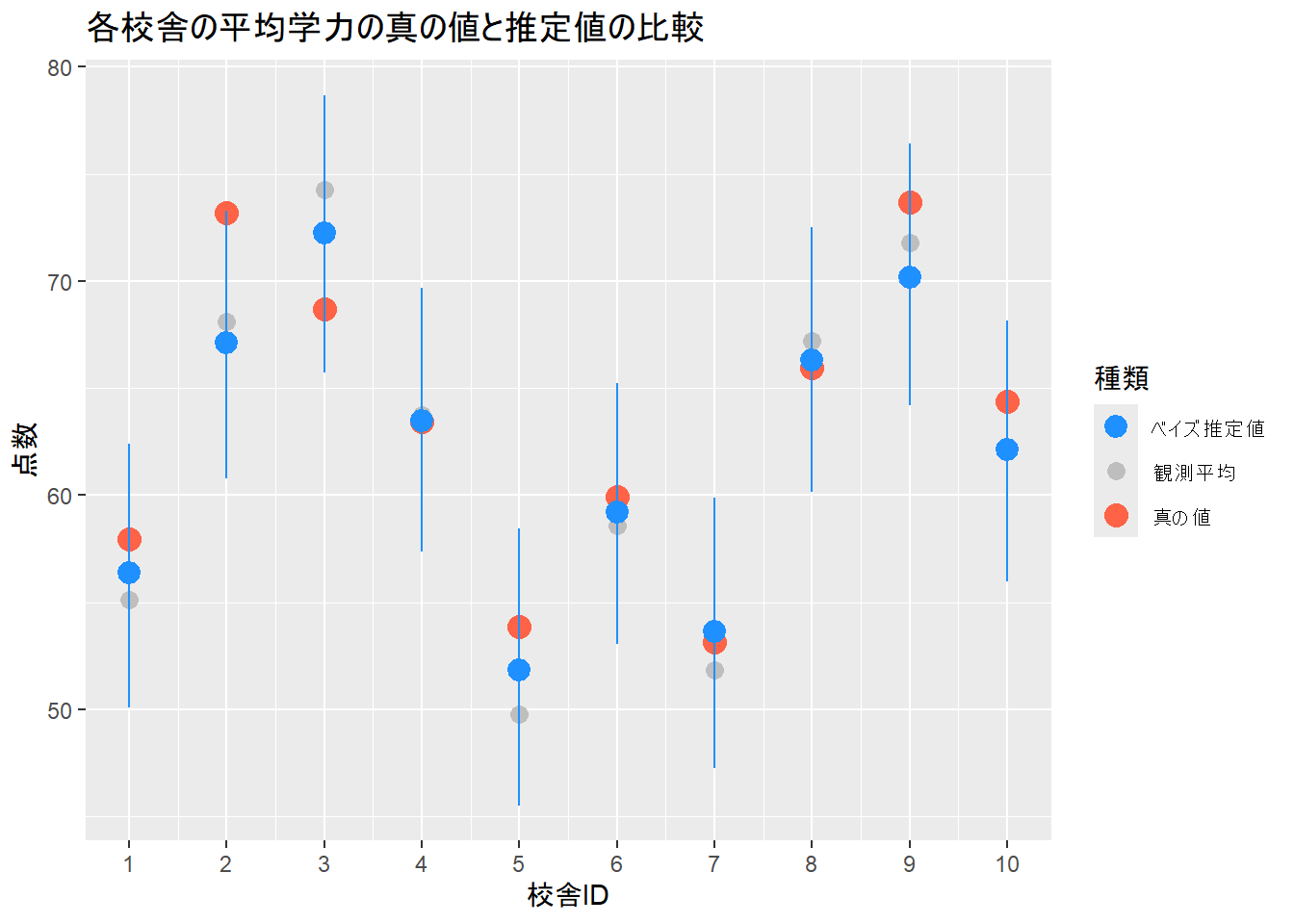
3. 真の値と推定値の比較
最後に、モデルが推定した校舎ごとの平均学力(theta)と、シミュレーションで設定した真のthetaを比較します。
ggplot(plot_data) +
geom_point(aes(x = school_id, y = raw_mean, colour = "観測平均"), size = 3) +
geom_point(aes(x = school_id, y = true_theta, colour = "真の値"), size = 4) +
geom_pointrange(aes(x = school_id, y = mean, ymin = q2.5, ymax = q97.5, colour = "ベイズ推定値"), size = 0.8) +
scale_x_continuous(breaks = 1:J) +
scale_color_manual(
name = "種類",
values = c("観測平均" = "gray", "真の値" = "tomato", "ベイズ推定値" = "dodgerblue"),
guide = guide_legend(override.aes = list(
linetype = c("blank", "blank", "solid")
))
) +
labs(
title = "各校舎の平均学力の真の値と推定値の比較",
x = "校舎ID", y = "点数"
)Figure 3 から、単純な観測平均(灰色の点)よりも、階層ベイズモデルによる推定値(青い点とエラーバー)の方が、真の値(赤い三角形)に近い校舎の数が遠い校舎の数を上回っていることを確認できます。
以上です。