Rでゴールドフェルド=クォント検定

Rで ゴールドフェルド=クォント検定 を試みます。

1. ゴールドフェルド=クォント検定とは

ゴールドフェルド=クォント検定（Goldfeld-Quandt Test）は、回帰分析の誤差項が不均一分散（Heteroscedasticity）の性質を持つかどうかを検定するための手法です。

検定の目的

回帰分析の基本的な仮定の一つに「誤差項の分散が均一である（等分散性）」という仮定があります。しかし、実際のデータでは、説明変数の値が大きくなるにつれて誤差のばらつき（分散）も大きくなる、といったケースが頻繁に見られます。このような不均一分散が存在すると、回帰係数の推定値の信頼性が低下するなどの問題が生じます。

ゴールドフェルド=クォント検定は、このような不均一分散を統計的に検出することを目的とします。

検定の仮説

帰無仮説 (H₀): 誤差項の分散は均一である（等分散性）。
対立仮説 (H₁): 誤差項の分散は均一ではない（不均一分散性）。特に、特定の変数と関連して分散が単調に増加または減少する。

検定の手順

データの並べ替え: 不均一分散の原因と疑われる説明変数（例えば x）の値が小さい順にデータを並べ替えます。
データ分割:
- 中央部分のデータ（c個）を取り除きます。これにより、分散が小さい可能性のあるグループと大きい可能性のあるグループの差が明確になります。
- 残ったデータを2つのグループ（前半のグループ1、後半のグループ2）に均等に分けます。
個別の回帰分析: グループ1とグループ2、それぞれで回帰分析を行い、それぞれの残差平方和（RSS₁ と RSS₂）を計算します。
F統計量の計算: 2つの残差平方和の比をとって、F統計量を計算します。説明変数 x が大きくなるにつれて分散が大きくなると想定する場合、F値は RSS₂ / RSS₁ となります。
判定: 計算されたF値が、対応する自由度を持つF分布において統計的に有意なほど大きい場合（p値が有意水準(本シミュレーションでは5%とします)より小さい場合）、帰無仮説を棄却します。つまり、「不均一分散が存在する」と結論付けます。

2. Rによるシミュレーション

それでは、実際にRを使ってシミュレーションを行います。ここでは、以下の2つのケースのデータを作成し、それぞれで検定を行います。

ケース1: 等分散のデータ (帰無仮説が正しい状況)
ケース2: 不均一分散のデータ (対立仮説が正しい状況)

準備：ライブラリのロード

まず、シミュレーションに必要なライブラリをロードします。

library(ggplot2)
library(lmtest) # ゴールドフェルド=クォント検定(gqtest)用
library(patchwork)

サンプルデータの作成

シミュレーションの再現性を確保するために、乱数のシードを固定します。

seed <- 20250703
set.seed(seed)

# データ点の数
n <- 200

# 説明変数 x を生成
x <- 1:n

# ケース1：等分散データの作成
# 誤差項の標準偏差が一定 (sd = 25)
u1 <- rnorm(n, mean = 0, sd = 25)
y1 <- 50 + 2 * x + u1
df_homo <- data.frame(x, y = y1, type = "等分散 (Homoscedastic)")

# ケース2：不均一分散データの作成
# 誤差項の標準偏差が x の値に比例して大きくなる (sd = 0.4 * x)
u2 <- rnorm(n, mean = 0, sd = 0.4 * x)
y2 <- 50 + 2 * x + u2
df_hetero <- data.frame(x, y = y2, type = "不均一分散 (Heteroscedastic)")

# 2つのデータフレームを結合
df_combined <- rbind(df_homo, df_hetero)

データの可視化

作成した2種類のデータをプロットして、見た目の違いを確認しましょう。

# ggplotで散布図を作成
p <- ggplot(df_combined, aes(x = x, y = y)) +
  geom_point(alpha = 0.6, color = "dodgerblue") + # データ点をプロット
  geom_smooth(method = "lm", se = FALSE, color = "firebrick", linetype = "dashed") + # 回帰直線を追加
  facet_wrap(~type, scales = "free_y") + # ケースごとにプロットを分ける
  labs(
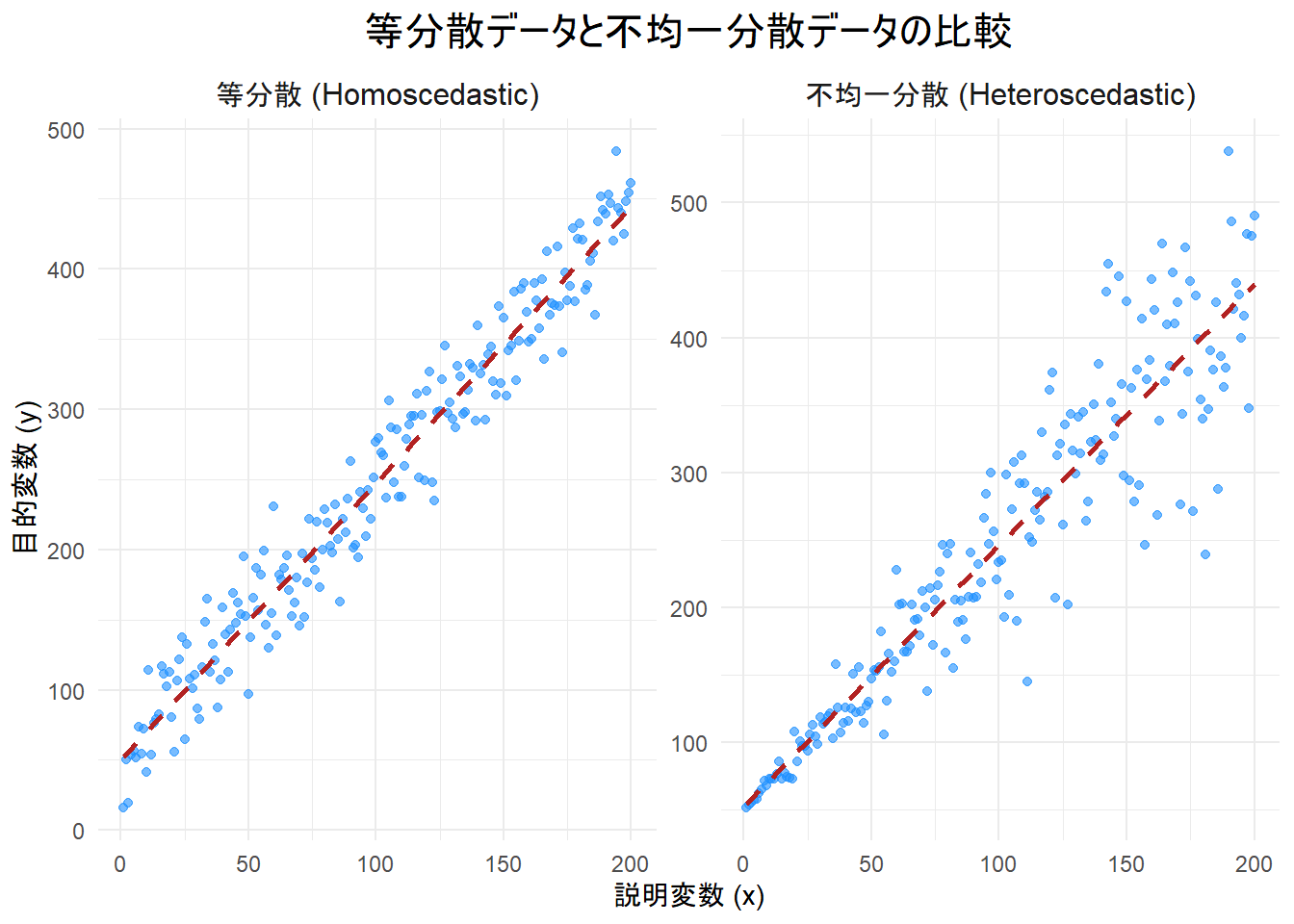
    title = "等分散データと不均一分散データの比較",
    x = "説明変数 (x)",
    y = "目的変数 (y)"
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(hjust = 0.5, size = 16),
    strip.text = element_text(size = 12)
  )

# プロットを表示
print(p)

プロットの解説

左側（等分散）: データ点は回帰直線の周りに均一にばらついています。
右側（不均一分散）: xが大きくなるにつれて、データ点の回帰直線からのばらつき（誤差）が大きくなっているのが見て取れます。

ゴールドフェルド=クォント検定の実行

lmtestパッケージのgqtest()関数を使って検定を実行します。

gqtest(model, order.by = ~x, fraction = 0.2)
- model: lm()で作成した回帰モデル。
- order.by: データを並べ替える基準となる変数（不均一分散の原因と疑う変数）を指定します。
- fraction: 中央から取り除くデータの割合を指定します。ここでは20%（0.2）とします。

ケース1: 等分散データでの検定

# 回帰モデルの構築
model_homo <- lm(y ~ x, data = df_homo)

# ゴールドフェルド=クォント検定の実行
gq_test_homo <- gqtest(model_homo, order.by = ~x, fraction = 0.2)

# 結果の表示
cat("--- ケース1：等分散データでの検定結果 ---\n")
print(gq_test_homo)

--- ケース1：等分散データでの検定結果 ---

    Goldfeld-Quandt test

data:  model_homo
GQ = 0.9099, df1 = 78, df2 = 78, p-value = 0.6611
alternative hypothesis: variance increases from segment 1 to 2

結果の解釈 (ケース1):

p-value = 0.6611 となりました。
これは定めた有意水準5%よりも大きいため、帰無仮説（誤差項は等分散である）を棄却できません。
この結果は、私たちが作成した等分散データと整合的であり、検定が正しく機能していることを示唆します。

ケース2: 不均一分散データでの検定

# 回帰モデルの構築
model_hetero <- lm(y ~ x, data = df_hetero)

# ゴールドフェルド=クォント検定の実行
gq_test_hetero <- gqtest(model_hetero, order.by = ~x, fraction = 0.2)

# 結果の表示
cat("--- ケース2：不均一分散データでの検定結果 ---\n")
print(gq_test_hetero)

--- ケース2：不均一分散データでの検定結果 ---

    Goldfeld-Quandt test

data:  model_hetero
GQ = 10.527, df1 = 78, df2 = 78, p-value < 2.2e-16
alternative hypothesis: variance increases from segment 1 to 2

結果の解釈 (ケース2):