Rでダービン=ワトソン検定

Rで ダービン=ワトソン検定 を試みます。

ダービン=ワトソン検定とは

ダービン=ワトソン（Durbin-Watson）検定は、回帰分析の結果得られた残差（誤差項）に自己相関（系列相関）が存在するかどうかを調べるための統計的検定です。

主に時系列データなど、データの順序に意味がある場合に用いられます。

なぜ重要か？

回帰分析の重要な仮定の一つに「残差の独立性（残差間に相関がない）」があります。もし残差に自己相関が存在すると、以下の問題が生じます。

係数の標準誤差が過小評価され、本来は有意でない説明変数を「有意である」と誤って判断してしまう可能性がある。
モデルの決定係数（R²）が実態よりも高く算出され、モデルの当てはまりを過大評価してしまう。

検定の仮説

ダービン=ワトソン検定では、主に「正の自己相関」を念頭に置いて、以下の仮説を検証します。

帰無仮説 (H₀): 残差に自己相関はない (自己相関係数 ρ = 0)。
対立仮説 (H₁): 残差に正の自己相関がある (自己相関係数 ρ > 0)。

検定統計量（d値）

検定には d比または d統計量 と呼ばれる値を用います。この値は0から4の範囲を取ります。

d ≈ 2 の場合: 自己相関はない（帰無仮説を採択）。
d ≈ 0 の場合: 正の自己相関がある（帰無仮説を棄却）。残差プロットは滑らかな波を描く傾向があります。
d ≈ 4 の場合: 負の自己相関がある（帰無仮説を棄却）。残差プロットはギザギザに符号が反転する傾向があります。

d値の判定には、サンプルサイズ(n)と説明変数の数(k)に応じた臨界値（dL, dU）を用いますが、Rのパッケージを使えばp値が計算されるため、本シミュレーションでは有意水準を5%としてp値を見て判断します。

Rによるシミュレーション

それでは、Rを使って「自己相関がない場合」と「正の自己相関がある場合」の2つのケースをシミュレーションし、ダービン=ワトソン検定の結果がどのように変わるかを見てみましょう。

準備：必要なパッケージのロード

lmtestはダービン=ワトソン検定に利用します。

# パッケージのロード
library(lmtest)
library(ggplot2)
library(dplyr)

ケース1：自己相関がないデータのシミュレーション

まず、理想的な状況、つまり残差に自己相関がないデータを作成して分析します。

1. データ作成

時間（x）と、正規乱数に従う誤差項（error）を持つデータを作成します。

seed <- 20250703
set.seed(seed)

# サンプルサイズ
n <- 100

# データ生成
df_no_autocor <- data.frame(
  x = 1:n,
  # 自己相関のない誤差項 (ホワイトノイズ)
  error = rnorm(n, mean = 0, sd = 10)
) %>%
  # y = 5 + 2*x + 誤差
  mutate(y = 5 + 2 * x + error)

2. 回帰分析とダービン・ワトソン検定

作成したデータで線形回帰モデルを作成し、dwtest()関数で検定を実行します。

# 線形回帰モデルの構築
model_no_autocor <- lm(y ~ x, data = df_no_autocor)

# ダービン=ワトソン検定の実行
dw_result_no_autocor <- dwtest(model_no_autocor)
cat("--- ダービン=ワトソン検定の結果 ---\n")
print(dw_result_no_autocor)

--- ダービン=ワトソン検定の結果 ---

    Durbin-Watson test

data:  model_no_autocor
DW = 1.8864, p-value = 0.2492
alternative hypothesis: true autocorrelation is greater than 0

結果の解釈:

DW（d値）= 1.8864: 2に近く、自己相関がないことを示唆しています。
p-value = 0.2492: p値が有意水準0.05より大きいため、帰無仮説（自己相関はない）を棄却できません。

3. 結果の可視化

残差のプロットとACF（自己相関関数）プロットを作成し、視覚的に確認します。

# 残差をデータフレームに追加
df_no_autocor$residuals <- residuals(model_no_autocor)

# 1. 残差プロット
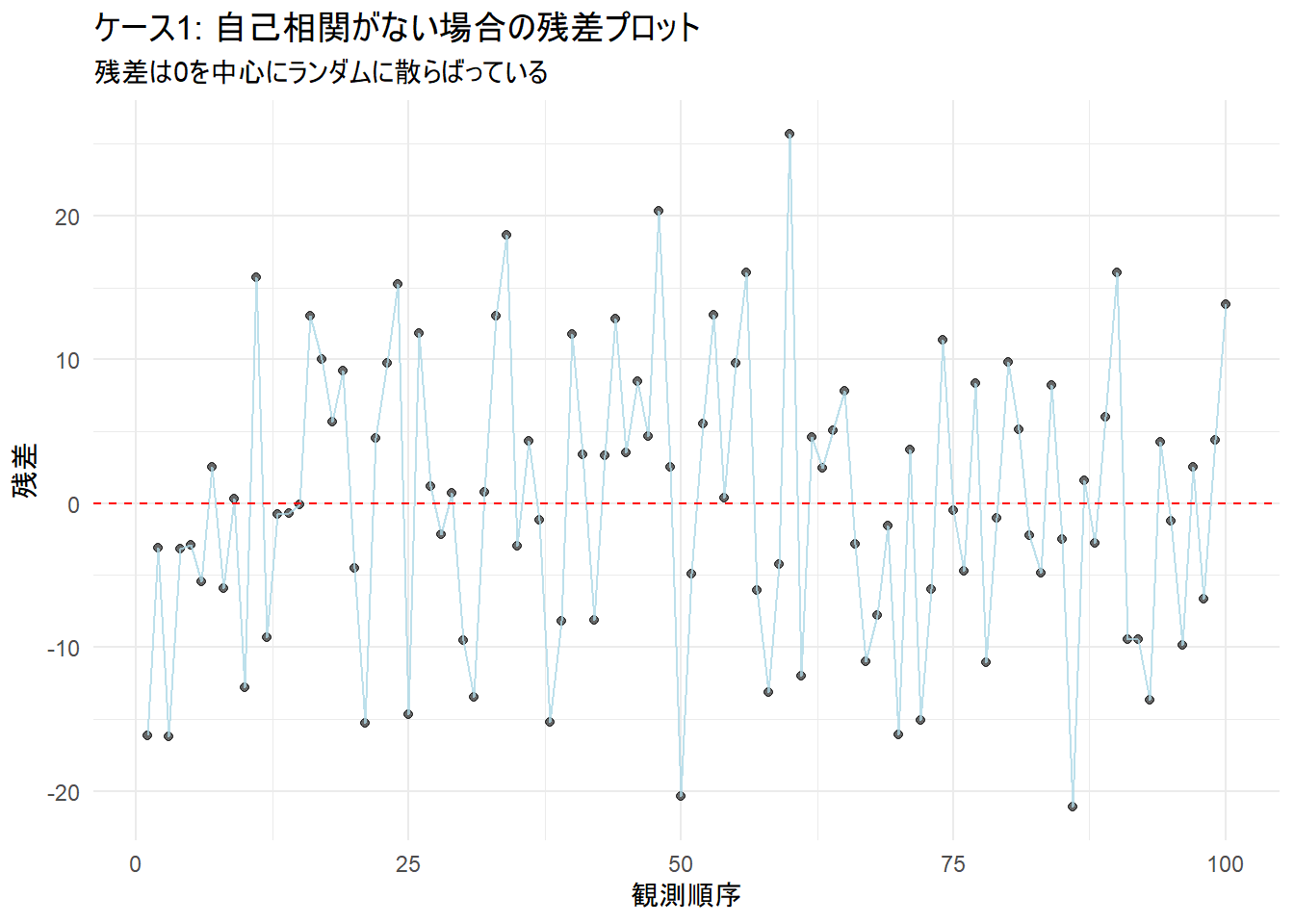
p1 <- ggplot(df_no_autocor, aes(x = x, y = residuals)) +
  geom_point(alpha = 0.6) +
  geom_line(color = "lightblue", alpha = 0.8) +
  geom_hline(yintercept = 0, linetype = "dashed", color = "red") +
  labs(
    title = "ケース1: 自己相関がない場合の残差プロット",
    subtitle = "残差は0を中心にランダムに散らばっている",
    x = "観測順序", y = "残差"
  ) +
  theme_minimal()

# 2. ACFプロット
# acf()で自己相関を計算し、ggplotで描画
acf_data_no_autocor <- acf(df_no_autocor$residuals, plot = FALSE)
df_acf_no_autocor <- data.frame(lag = acf_data_no_autocor$lag, acf = acf_data_no_autocor$acf)

# 95%信頼区間の線を計算
ci_95 <- qnorm((1 + 0.95) / 2) / sqrt(n)

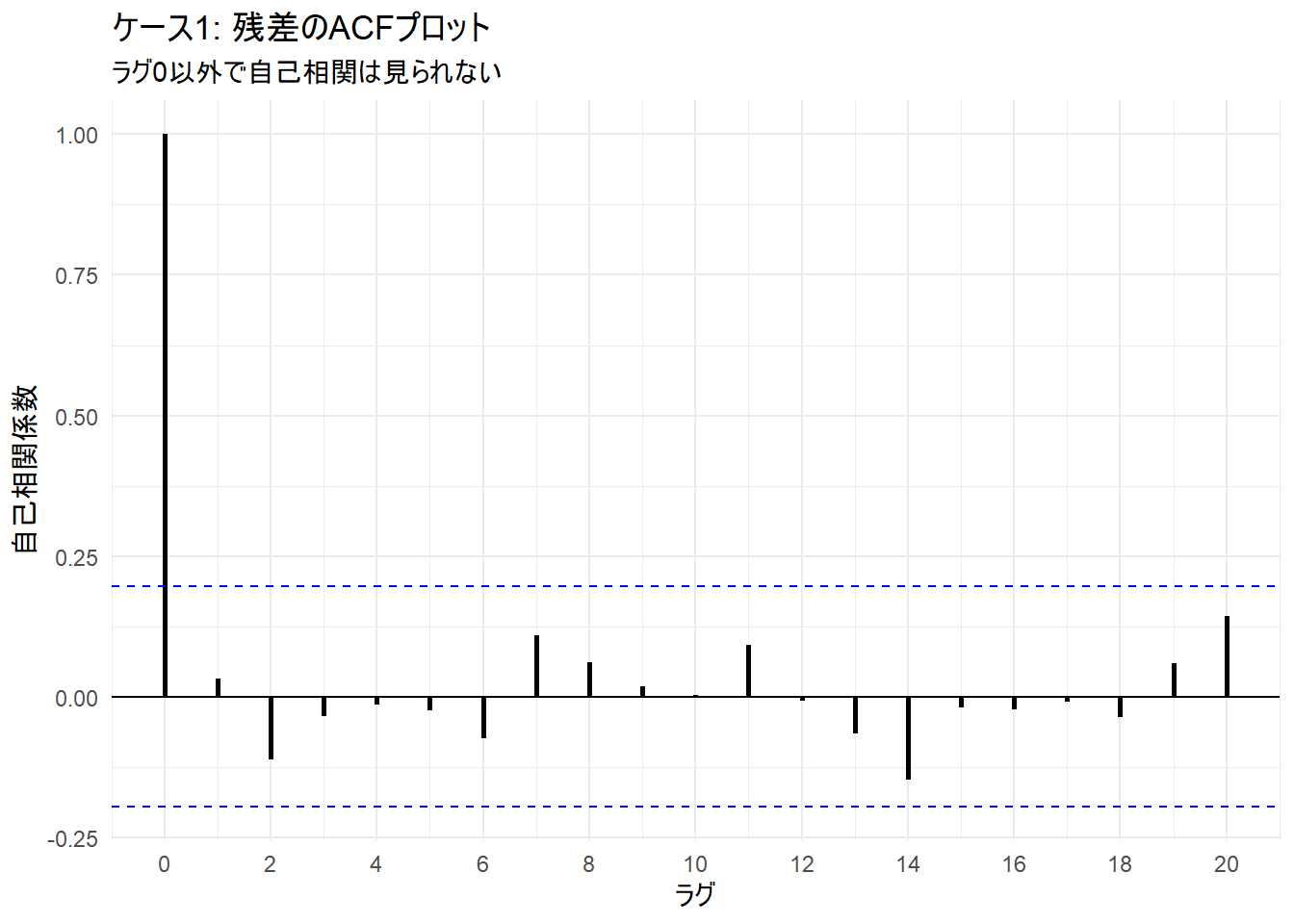
p2 <- ggplot(df_acf_no_autocor, aes(x = lag, y = acf)) +
  geom_hline(aes(yintercept = 0)) +
  geom_segment(aes(xend = lag, yend = 0), size = 1) +
  geom_hline(yintercept = c(ci_95, -ci_95), linetype = "dashed", color = "blue") +
  labs(
    title = "ケース1: 残差のACFプロット",
    subtitle = "ラグ0以外で自己相関は見られない",
    x = "ラグ", y = "自己相関係数"
  ) +
  scale_x_continuous(breaks = seq(0, max(df_acf_no_autocor$lag), by = 2)) +
  theme_minimal()

# プロットを表示
print(p1)
print(p2)

プロットの解釈:

残差プロット: 残差が0の周りで特定のパターンなく、ランダムに散らばっていることが分かります(Figure 1)。
ACFプロット: ラグ0（自分自身との相関）を除き、すべての自己相関係数が青い点線の信頼区間内に収まっており、統計的に有意な自己相関はないと判断できます(Figure 2)。

ケース2：正の自己相関があるデータのシミュレーション

次に、残差に意図的に正の自己相関を持たせたデータで、検定がどう機能するかを確認します。

1. データ作成

AR(1)モデル（1期前の誤差が現在の誤差に影響を与えるモデル）を用いて、自己相関のある誤差項を生成します。

set.seed(seed)

# 自己相関係数 (0に近いほど弱く、1に近いほど強い)
rho <- 0.8

# 自己相関のある誤差項を生成
# e[t] = rho * e[t-1] + noise
error_autocor <- as.vector(arima.sim(model = list(ar = rho), n = n, sd = 10))

# データ生成
df_autocor <- data.frame(
  x = 1:n,
  error = error_autocor
) %>%
  mutate(y = 5 + 2 * x + error)

2. 回帰分析とダービン・ワトソン検定

# 線形回帰モデルの構築
model_autocor <- lm(y ~ x, data = df_autocor)

# ダービン=ワトソン検定の実行
dw_result_autocor <- dwtest(model_autocor)
cat("--- ダービン=ワトソン検定の結果 ---\n")
print(dw_result_autocor)

--- ダービン=ワトソン検定の結果 ---

    Durbin-Watson test

data:  model_autocor
DW = 0.45689, p-value = 1.403e-15
alternative hypothesis: true autocorrelation is greater than 0

結果の解釈:

DW（d値）= 0.45689: 0に近く、正の自己相関があることを示唆しています。
p-value = 1.403e-15: p値が設定した有意水準より小さく、帰無仮説は棄却されます。したがって、「正の自己相関がある」と結論付けられます。

3. 結果の可視化

# 残差をデータフレームに追加
df_autocor$residuals <- residuals(model_autocor)

# 1. 残差プロット
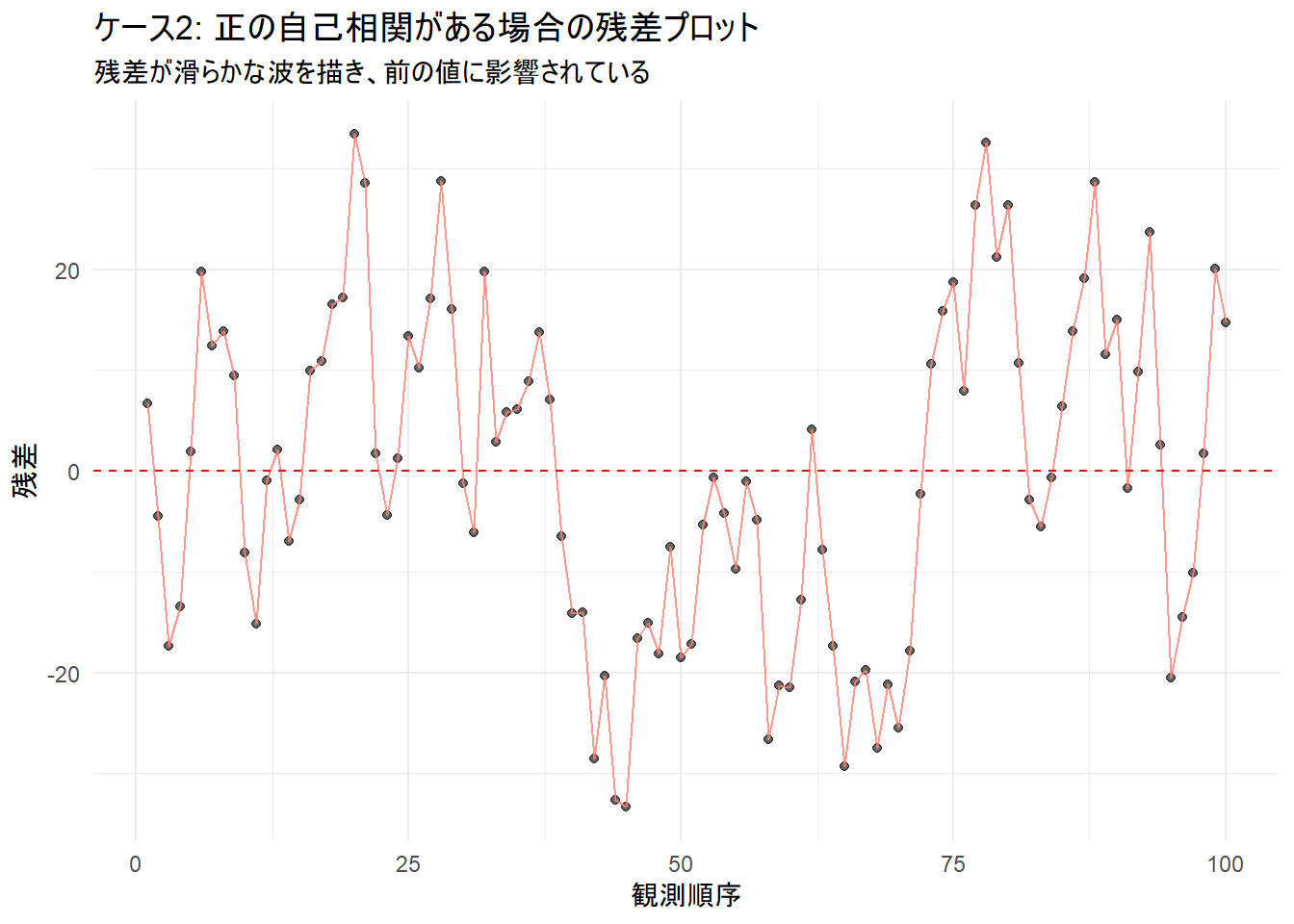
p3 <- ggplot(df_autocor, aes(x = x, y = residuals)) +
  geom_point(alpha = 0.6) +
  geom_line(color = "salmon", alpha = 0.8) +
  geom_hline(yintercept = 0, linetype = "dashed", color = "red") +
  labs(
    title = "ケース2: 正の自己相関がある場合の残差プロット",
    subtitle = "残差が滑らかな波を描き、前の値に影響されている",
    x = "観測順序", y = "残差"
  ) +
  theme_minimal()

# 2. ACFプロット
acf_data_autocor <- acf(df_autocor$residuals, plot = FALSE)
df_acf_autocor <- data.frame(lag = acf_data_autocor$lag, acf = acf_data_autocor$acf)

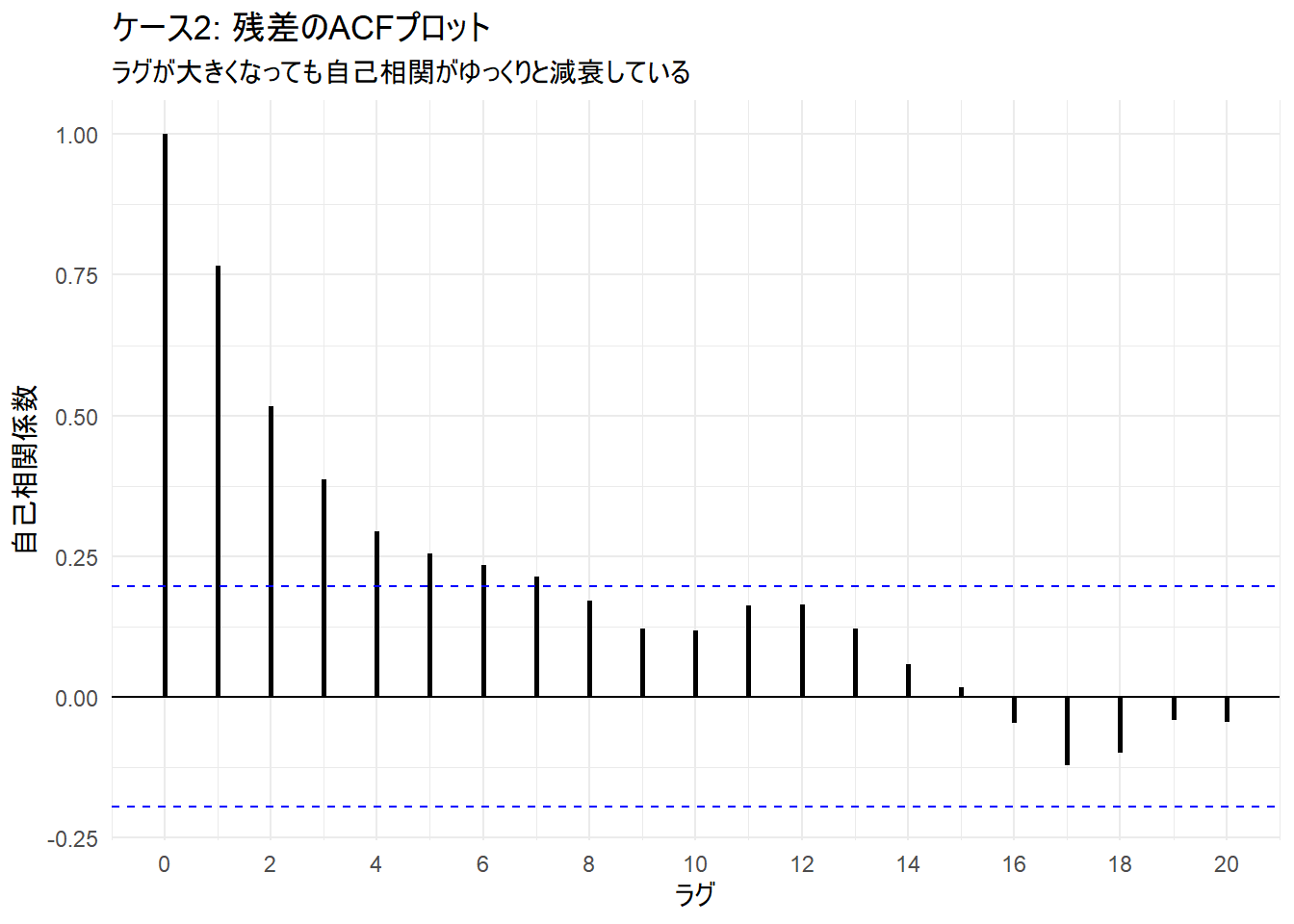
p4 <- ggplot(df_acf_autocor, aes(x = lag, y = acf)) +
  geom_hline(aes(yintercept = 0)) +
  geom_segment(aes(xend = lag, yend = 0), size = 1) +
  geom_hline(yintercept = c(ci_95, -ci_95), linetype = "dashed", color = "blue") +
  labs(
    title = "ケース2: 残差のACFプロット",
    subtitle = "ラグが大きくなっても自己相関がゆっくりと減衰している",
    x = "ラグ", y = "自己相関係数"
  ) +
  scale_x_continuous(breaks = seq(0, max(df_acf_autocor$lag), by = 2)) +
  theme_minimal()

# プロットを表示
print(p3)
print(p4)

プロットの解釈:

残差プロット: 残差がランダムではなく、滑らかな波のようなパターンを描いています。正の値が続いた後には正の値が、負の値が続いた後には負の値が出やすい、という正の自己相関の特徴がはっきりと見て取れます(Figure 3)。
ACFプロット: ラグ1の自己相関が高く、その後もゆっくりとしか減衰していません。1から7次までのラグで自己相関係数が信頼区間を大きく超えており、自己相関の存在を裏付けています(Figure 4)。

まとめ

このシミュレーションから、ダービン=ワトソン検定が回帰モデルの残差における自己相関をいかに効果的に検出するかが分かります。

項目	ケース1 (自己相関なし)	ケース2 (正の自己相関あり)
DW (d値)	1.8864 (約2)	0.45689 (約0)
p値	0.2492 (> 0.05)	1.403e-15 (< 0.05)
検定結果	自己相関なし(H₀) を棄却できず	正の自己相関あり (H₀棄却)
残差プロット	ランダムな散らばり	滑らかな波状のパターン
ACFプロット	ラグ0以外は信頼区間内	高い自己相関がゆっくり減衰