Rで平均への回帰

Rで 平均への回帰 を確認します。

1. 「平均への回帰」とは？

「平均への回帰（Regression to the mean）」とは、1回目の測定で極端な値（非常に良い、または非常に悪い値）を示したものは、2回目の測定ではより平均に近い値になる傾向があるという統計的な現象です。

これは、何らかの超自然的な力や因果関係が働いているわけではありません。多くの場合、測定値は以下の2つの要素で構成されていると考えることができます。

測定値 = 真の値（実力など） + 偶然の変動（運、誤差など）

例えば、あるテストで満点に近い点数を取った学生がいたとします。その学生は元々実力が高いのに加え、その日の体調が非常に良かったり、ヤマが当たったりといった「偶然の幸運」が重なった結果である可能性が高いです。次に同じようなテストを受けた際、実力は変わりませんが、前回と同じような「偶然の幸運」が再び起こる可能性は低いため、点数は少し下がり、より平均的な点数に近づく傾向があります。

逆に、非常に悪い点数を取った学生は、実力不足に加えて「偶然の不運」（体調不良、ケアレスミスなど）が重なったのかもしれません。次回のテストでは、その不運が繰り返される可能性は低いため、点数は上がり、平均に近づくことが期待されます。

この現象を知らないと、以下のような誤った解釈をしてしまう可能性があります。

誤解の例: 「成績が非常に良かった生徒を褒めたら、次のテストで成績が下がった。褒めるのは逆効果だ。」
現象の説明: その生徒の成績は、もともと「平均への回帰」によって下がる可能性が高かっただけで、褒めたこととは直接の因果関係はないかもしれません。

それでは、この現象をシミュレーションで確認してみましょう。

2. R言語によるシミュレーション

学生たちの2回のテスト結果をシミュレーションし、「平均への回帰」を可視化します。

ステップ1: 必要なライブラリの読み込みと準備

まず、データの処理と可視化に必要なライブラリを読み込みます。

library(ggplot2)
library(dplyr)

seed <- 20250704

ステップ2: サンプルデータの作成

1000人の学生のデータを作成します。各学生には「真の学力」があり、各テストの結果は「真の学力」に「偶然の変動（誤差）」が加わって決まると仮定します。

真の学力 (true_ability): 平均50点、標準偏差10点の正規分布に従う。
偶然の変動 (random_error): 平均0点、標準偏差15点の正規分布に従う。偶然の要素を大きくすることで、現象を分かりやすくします。

set.seed(seed)

# 学生の数
n_students <- 1000

# データフレームの作成
sim_data <- data.frame(
  student_id = 1:n_students
)

# 1. 各学生の「真の学力」を生成
sim_data$true_ability <- rnorm(n_students, mean = 50, sd = 10)

# 2. 2回分のテストの「偶然の変動」を生成
sim_data$error1 <- rnorm(n_students, mean = 0, sd = 15)
sim_data$error2 <- rnorm(n_students, mean = 0, sd = 15)

# 3. テストの点数を計算 (学力 + 偶然)
sim_data$test1_score <- sim_data$true_ability + sim_data$error1
sim_data$test2_score <- sim_data$true_ability + sim_data$error2

# 念のため、点数が0-100の範囲に収まるように調整
sim_data <- sim_data %>%
  mutate(
    test1_score = pmin(100, pmax(0, test1_score)),
    test2_score = pmin(100, pmax(0, test2_score))
  )

cat("--- データの一部を確認 ---\n")
head(sim_data)

--- データの一部を確認 ---
  student_id true_ability     error1     error2 test1_score test2_score
1          1     58.92313  -7.410224 -13.856590    51.51291    45.06654
2          2     44.36029  19.542277  18.341408    63.90257    62.70170
3          3     51.38700   8.540780  23.067644    59.92778    74.45464
4          4     59.24305 -13.145179   2.166961    46.09787    61.41001
5          5     67.43704  -8.231909   3.800086    59.20513    71.23713
6          6     56.69751  22.700909  -1.189423    79.39842    55.50809

ステップ3: 全体像の可視化

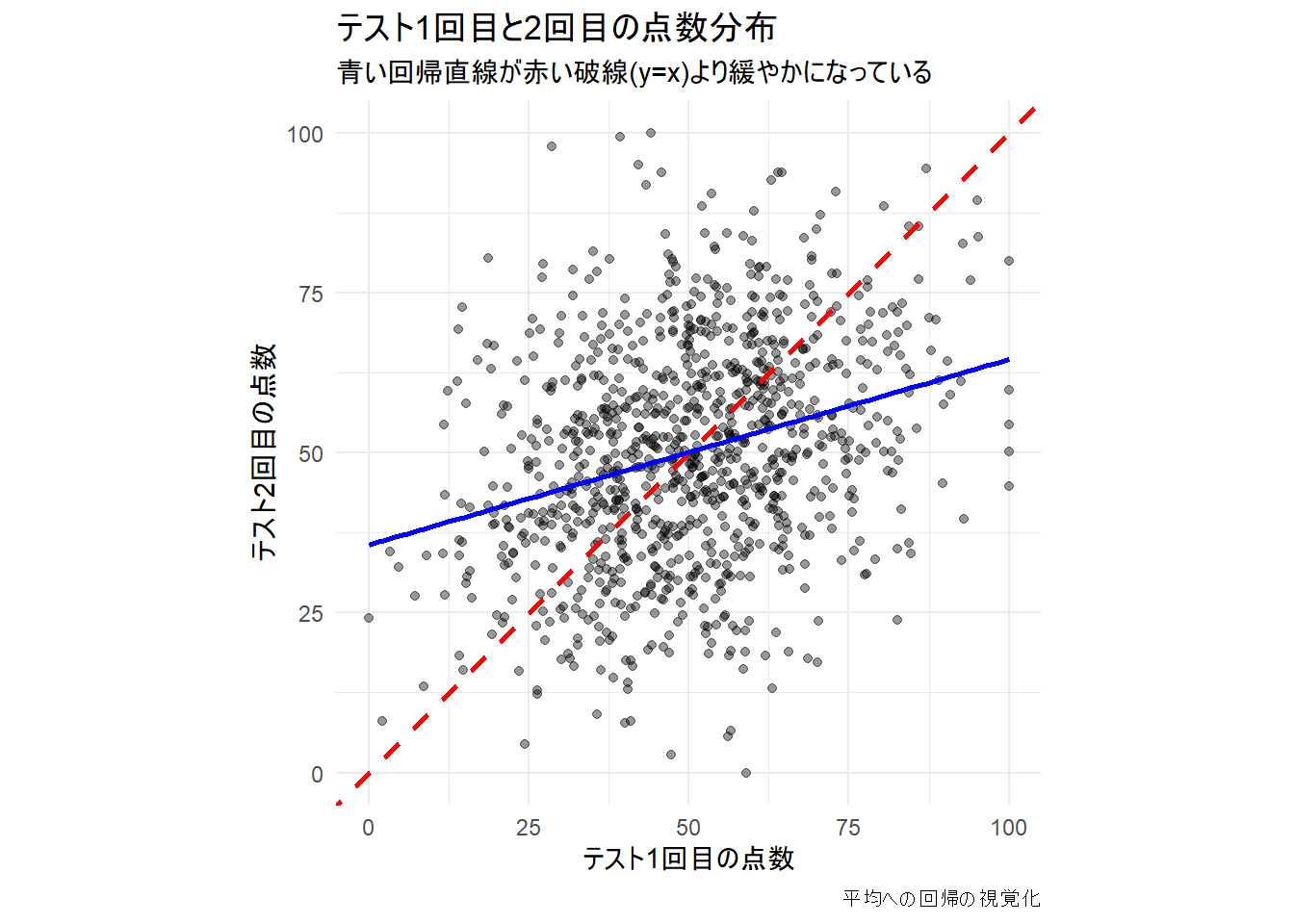
まず、1回目のテスト（test1_score）と2回目のテスト（test2_score）の関係を散布図で見てみましょう。

赤い破線 (y = x): もし平均への回帰がなければ、多くの点はこの線の周りに分布するはずです（1回目と2回目の点数がほぼ同じ）。
青い実線 (回帰直線): データ全体の傾向を示します。

ggplot(sim_data, aes(x = test1_score, y = test2_score)) +
  geom_point(alpha = 0.4) +
  # y = x の補助線 (もし平均への回帰がなければこの線に沿う)
  geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed", linewidth = 1) +
  # データ全体の傾向を示す回帰直線
  geom_smooth(method = "lm", se = FALSE, color = "blue", size = 1) +
  labs(
    title = "テスト1回目と2回目の点数分布",
    subtitle = "青い回帰直線が赤い破線(y=x)より緩やかになっている",
    x = "テスト1回目の点数",
    y = "テスト2回目の点数",
    caption = "平均への回帰の視覚化"
  ) +
  theme_minimal() +
  coord_fixed(xlim = c(0, 100), ylim = c(0, 100)) # 軸のスケールを揃える

Figure 1 から、青い回帰直線が赤い破線（y=x）よりも傾きが緩やかであることがわかります。これは、1回目で高い点数を取った学生は2回目で少し点数が下がる傾向があり、逆に1回目で低い点数を取った学生は2回目で点数が上がる傾向があることを示しています。これが「平均への回帰」です。

ステップ4: 上位・下位グループの分析

次に、1回目のテストで特に成績が良かったグループと悪かったグループに絞って、彼らの点数が2回目でどう変化したかを見てみましょう。

1回目のテスト結果に基づき、学生を「上位10%」、「下位10%」、「その他」に分類します。
各グループの1回目と2回目の平均点を計算します。
グループごとに色分けした散布図を作成します。

# 1. 1回目のテストの点数で上位/下位10%の閾値を計算
quantiles <- quantile(sim_data$test1_score, probs = c(0.1, 0.9))
lower_threshold <- quantiles[1]
upper_threshold <- quantiles[2]

# 2. 学生をグループ分け
sim_data_grouped <- sim_data %>%
  mutate(group = case_when(
    test1_score <= lower_threshold ~ "下位10%",
    test1_score >= upper_threshold ~ "上位10%",
    TRUE ~ "その他"
  )) %>%
  # プロットのために因子型に変換し、順序を整理
  mutate(group = factor(group, levels = c("上位10%", "その他", "下位10%")))

# 3. 各グループの平均点を計算して表示
summary_stats <- sim_data_grouped %>%
  filter(group != "その他") %>%
  group_by(group) %>%
  summarise(
    mean_test1 = mean(test1_score),
    mean_test2 = mean(test2_score),
    count = n()
  )
cat("--- 上位10%グループと下位10%グループの2回のテストの平均点 ---\n")
print(summary_stats)

--- 上位10%グループと下位10%グループの2回のテストの平均点 ---
# A tibble: 2 × 4
  group   mean_test1 mean_test2 count
  <fct>        <dbl>      <dbl> <int>
1 上位10%       81.5       59.0   100
2 下位10%       20.4       41.7   100

この結果は非常に明確です。

上位10%グループ: 1回目の平均点は 81.5点 でしたが、2回目では 59.0点 に下がっています。
下位10%グループ: 1回目の平均点は 20.4点 でしたが、2回目では 41.7点 に上がっています。

両グループとも、2回目のテストでは全体の平均（約50点）に近づいていることがわかります。

最後に、この結果を散布図で可視化します。

ggplot(sim_data_grouped, aes(x = test1_score, y = test2_score, color = group)) +
  geom_point(alpha = 0.7) +
  # y = x の補助線
  geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed") +
  # 各グループの平均点の変化を示す矢印
  geom_segment(
    data = summary_stats,
    aes(x = mean_test1, y = mean_test1, xend = mean_test1, yend = mean_test2),
    arrow = arrow(length = unit(0.3, "cm")),
    size = 1.2
  ) +
  scale_color_manual(values = c("上位10%" = "darkorange", "下位10%" = "steelblue", "その他" = "grey")) +
  labs(
    title = "上位・下位グループにおける平均への回帰",
    subtitle = "矢印は各グループの平均点の変化を示す (1回目 → 2回目)",
    x = "テスト1回目の点数",
    y = "テスト2回目の点数",
    color = "1回目の成績"
  ) +
  theme_minimal() +
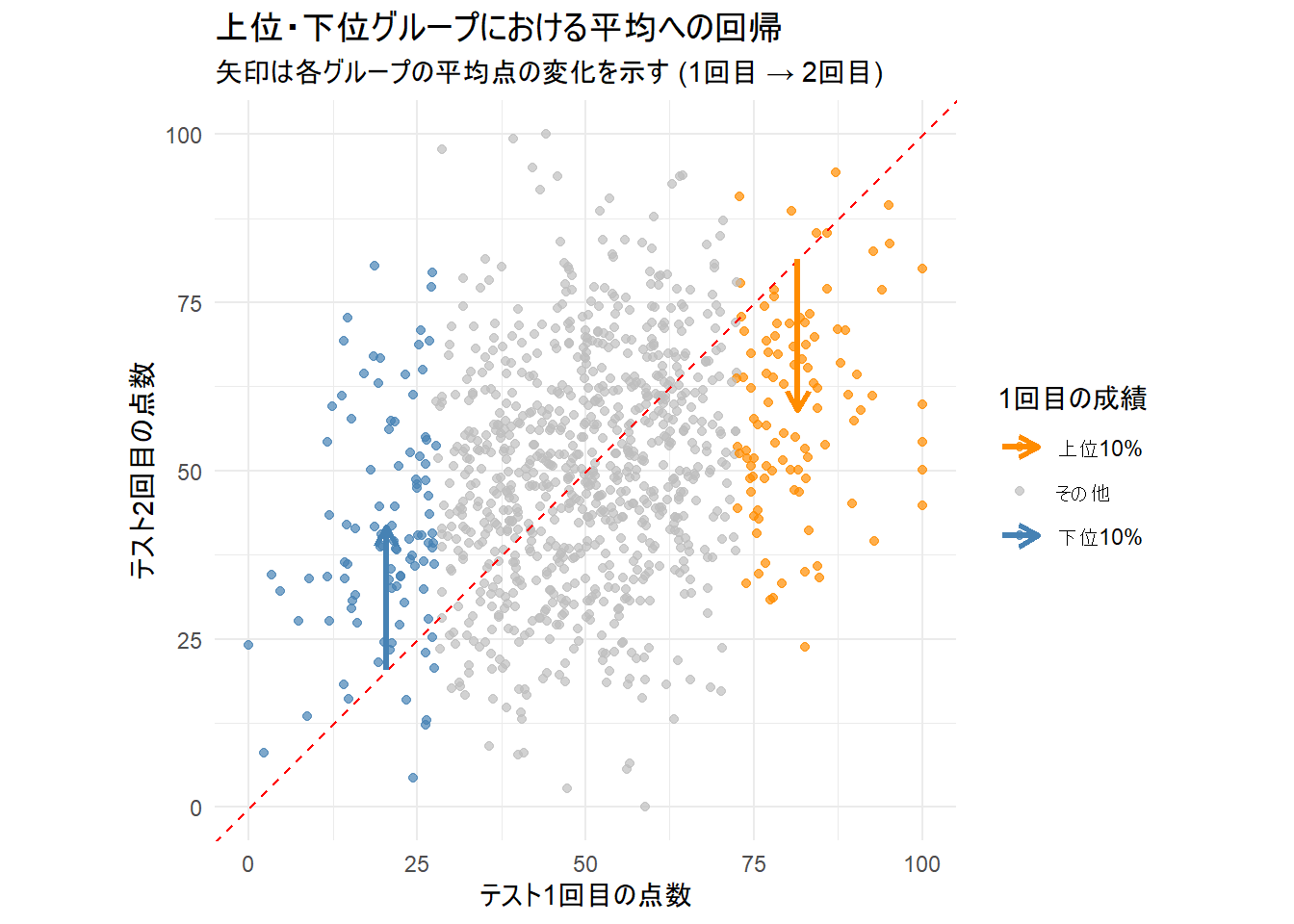
  coord_fixed(xlim = c(0, 100), ylim = c(0, 100))