Rで大数の弱法則と強法則

Rで 大数の弱法則と強法則 を確認します。

1. 大数の法則とは

大数の法則（Law of Large Numbers）は、「サンプルサイズが大きくなるにつれて、その標本平均は母平均に近づく」という、統計学および確率論における基本的な定理です。これには「弱法則」と「強法則」の2種類があり、収束の仕方の数学的な定義が異なります。

大数の弱法則 (Weak Law of Large Numbers, WLLN)

大数の弱法則は、標本平均が母平均に「確率収束」することを示します。

平易な言葉で説明すると、「サンプルサイズ n を十分に大きくすれば、標本平均が母平均から（どんなに小さく定めた値εよりも）大きく外れてしまう確率は、限りなく0に近づく」ということです。

数式で表現すると、標本平均を \(\bar{X}_n\)、母平均を \(\mu\)、任意の小さな正の数を \(\epsilon\) としたとき、以下が成り立ちます。 \[ \lim_{n \to \infty} P(|\bar{X}_n - \mu| > \epsilon) = 0 \] この法則は、個々の試行系列が必ずしも母平均に収束することを保証するわけではありません。あくまで「大きく外れる確率」が0に収束すると主張しているに過ぎません。

大数の強法則 (Strong Law of Large Numbers, SLLN)

大数の強法則は、標本平均が母平均に「ほとんど確実に収束（概収束）」することを示します。

平易な言葉で説明すると、「サンプルサイズ n を無限に大きくしていく試行を一度行うと、その過程で得られる標本平均の列は、最終的に（確率1で）母平均に収束する」ということです。

数式で表現すると、以下が成り立ちます。 \[ P(\lim_{n \to \infty} \bar{X}_n = \mu) = 1 \] こちらは弱法則よりも強力な主張です。試行の系列（サンプルパス）そのものが、収束しないという例外的なケースが起こる確率が0であると述べています。実用上、強法則が成り立てば、試行を続ければ続けるほど、標本平均は母平均に必ず落ち着くと考えてよいでしょう。

まとめ

法則	収束の種類	説明
弱法則	確率収束	サンプルサイズを増やすと、標本平均が母平均から外れる「確率」が0に近づく。
強法則	ほとんど確実な収束	サンプルサイズを増やす試行をすれば、標本平均という「値の系列そのもの」が（確率1で）母平均に収束する。

強法則が成立するならば、弱法則も成立します。

2. Rによるシミュレーション

シミュレーションを通じて、これらの法則を視覚的に理解してみましょう。ここでは、最も単純な例として「公正なコイン投げ」を考えます。表を1、裏を0とすると、この試行の母平均（期待値）は 0.5 です。

準備

まず、プロット作成に必要なggplot2ライブラリをロードします。

library(ggplot2)

# シミュレーションの再現性を確保するために乱数のシードを設定
seed <- 20250707

シミュレーション1: 大数の強法則の可視化

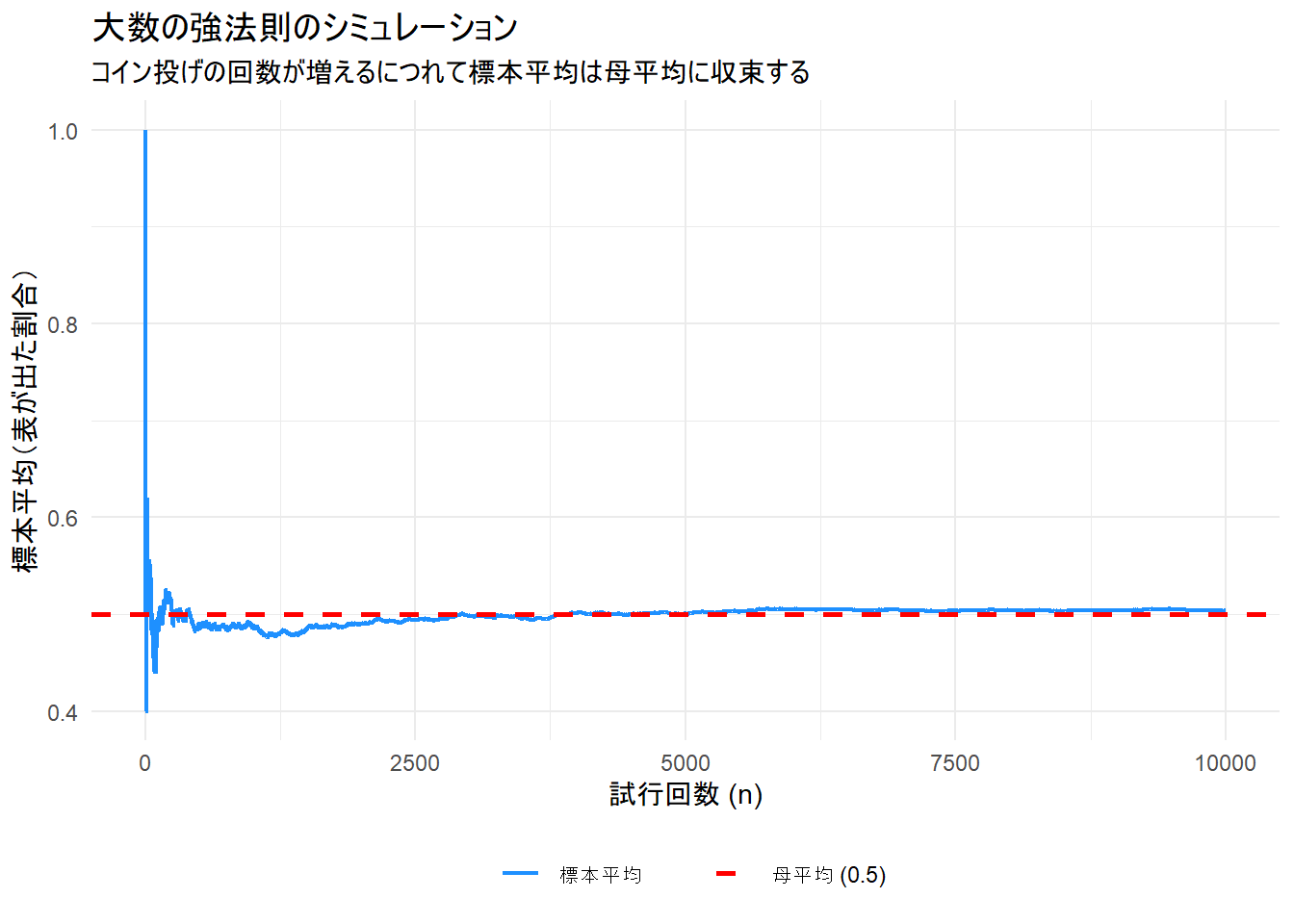
強法則は「1つの試行系列が、回数を重ねるごとに母平均に収束していく」様子を示します。ここでは、コイン投げを10,000回行い、各時点での「表が出た割合（標本平均）」がどのように推移するかを観察します。

set.seed(seed)

# パラメータ設定
n_trials <- 10000 # コイン投げの回数
prob_heads <- 0.5 # 母平均（表が出る確率）

# シミュレーションの実行
# 10,000回のコイン投げ（1:表, 0:裏）をシミュレート
coin_flips <- rbinom(n_trials, 1, prob_heads)

# 各時点までの累積平均を計算
# cumsum()は累積和を計算する関数
cumulative_means <- cumsum(coin_flips) / 1:n_trials

# プロット用のデータフレームを作成
slln_df <- data.frame(
  trial_number = 1:n_trials,
  sample_mean = cumulative_means
)

# プロットの作成
ggplot(slln_df, aes(x = trial_number, y = sample_mean)) +
  geom_line(aes(color = "標本平均"), linewidth = 0.8) +
  geom_hline(aes(yintercept = prob_heads, linetype = "母平均 (0.5)"), color = "red", linewidth = 1) +
  labs(
    title = "大数の強法則のシミュレーション",
    subtitle = "コイン投げの回数が増えるにつれて標本平均は母平均に収束する",
    x = "試行回数 (n)",
    y = "標本平均（表が出た割合）"
  ) +
  scale_color_manual(name = "", values = c("標本平均" = "dodgerblue")) +
  scale_linetype_manual(name = "", values = c("母平均 (0.5)" = "dashed")) +
  theme_minimal() +
  theme(legend.position = "bottom")

考察: Figure 1 を見ると、試行回数が少ないうちは標本平均が大きく変動していますが、回数が増える（横軸が進む）につれて、その変動は徐々に小さくなり、母平均である0.5の赤い破線に収束していく様子がはっきりとわかります。これが「ほとんど確実な収束」の視覚的なイメージです。

シミュレーション2: 大数の弱法則の可視化

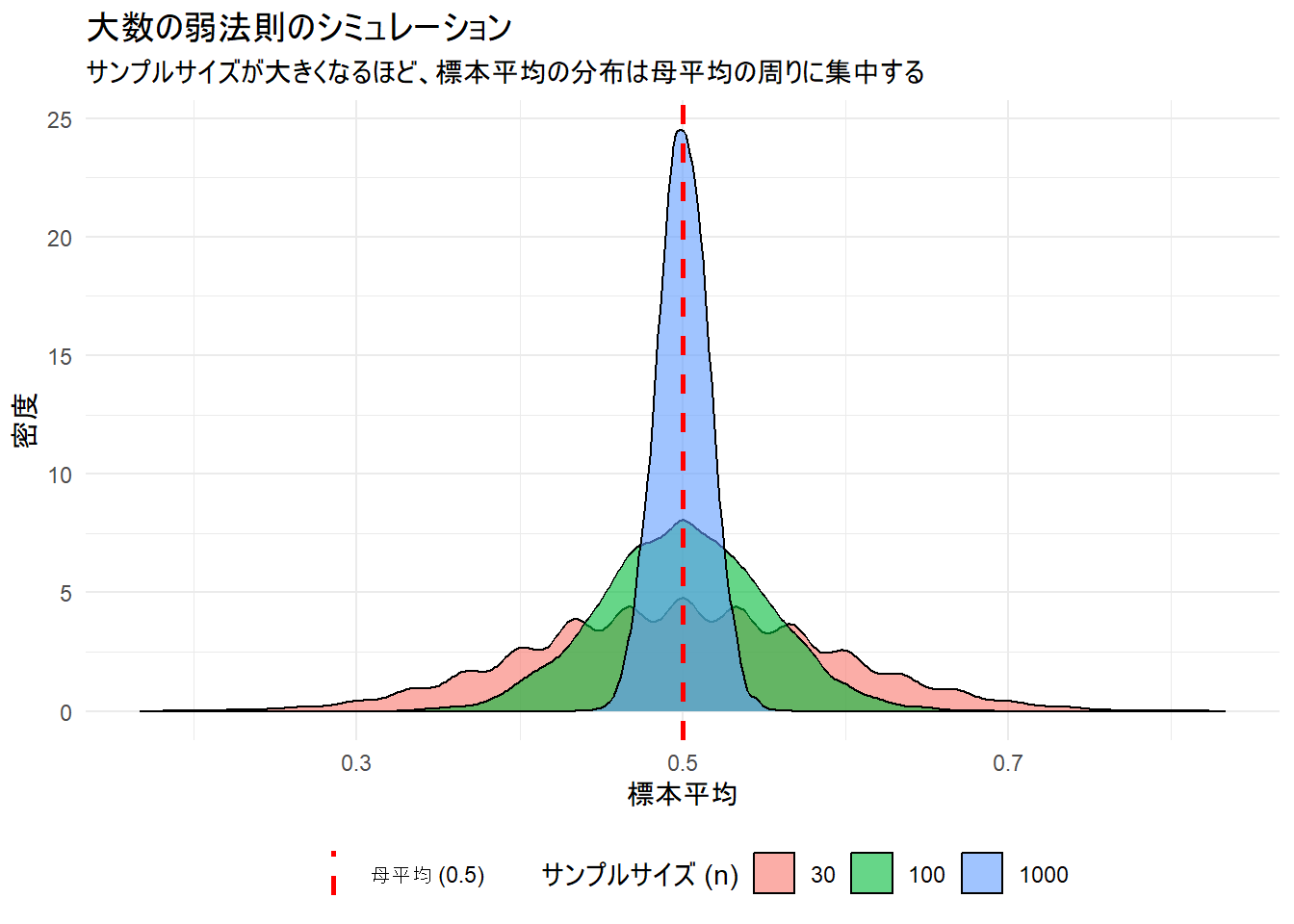
弱法則は「サンプルサイズが大きくなるほど、標本平均のばらつきが小さくなる（分布が母平均の周りに集中する）」ことを示します。これを可視化するために、異なるサンプルサイズ（n=30, 100, 1000）で何度も実験を繰り返し、それぞれの標本平均がどのように分布するかを比較します。

set.seed(seed)

# パラメータ設定
n_sims <- 10000 # 各サンプルサイズで行うシミュレーションの回数
sample_sizes <- c(30, 100, 1000) # 比較するサンプルサイズ
prob_heads <- 0.5 # 母平均

# シミュレーションの実行
# lapplyを使って各サンプルサイズでシミュレーションを行う
results <- lapply(sample_sizes, function(n) {
  # replicateで指定回数（n_sims）だけ、標本平均の計算を繰り返す
  means <- replicate(n_sims, {
    mean(rbinom(n, 1, prob_heads))
  })

  # 結果をデータフレームで返す
  data.frame(
    sample_mean = means,
    sample_size = as.factor(n)
  )
})

# 結果を一つのデータフレームに結合
wlln_df <- do.call(rbind, results)


# プロットの作成
ggplot(wlln_df, aes(x = sample_mean, fill = sample_size)) +
  geom_density(alpha = 0.6) +
  geom_vline(aes(xintercept = prob_heads, linetype = "母平均 (0.5)"), color = "red", linewidth = 1) +
  labs(
    title = "大数の弱法則のシミュレーション",
    subtitle = "サンプルサイズが大きくなるほど、標本平均の分布は母平均の周りに集中する",
    x = "標本平均",
    y = "密度",
    fill = "サンプルサイズ (n)"
  ) +
  scale_linetype_manual(name = "", values = c("母平均 (0.5)" = "dashed")) +
  theme_minimal() +
  theme(legend.position = "bottom")