Rで Lasso回帰とRidge回帰 を確認します。
Lasso回帰とRidge回帰について
Lasso回帰とRidge回帰は、どちらも通常の線形回帰(最小二乗法)に「正則化」と呼ばれるペナルティ項を追加した手法です。この正則化により、特に以下のような状況で有効なモデルを構築できます。
- 説明変数の数が多い: 説明変数の数がサンプルサイズに比べて多い場合、モデルがデータに過剰に適合してしまう「過学習(Overfitting)」が起こりやすくなります。
- 多重共線性: 説明変数間に強い相関がある場合、モデルの係数が不安定になり、解釈が難しくなります。
正則化は、モデルの係数(回帰係数 β)が大きくなりすぎるのを防ぐためのペナルティを損失関数に加えることで、モデルの複雑さを抑制し、過学習を防ぎます。
Ridge回帰 (L2正則化)
Ridge回帰は、損失関数に回帰係数の二乗和(L2ノルム)をペナルティ項として加えます。
目的関数: \[
\text{最小化する値} = \sum_{i=1}^{n}(y_i - \hat{y}_i)^2 + \lambda \sum_{j=1}^{p} \beta_j^2
\]
- 第1項は通常の最小二乗法と同じ、実測値と予測値の誤差の二乗和です。
- 第2項がRidge回帰のペナルティ項で、\(\lambda\)(ラムダ)はペナルティの強さを調整するハイパーパラメータです。
- \(\beta_j\) は各説明変数の回帰係数です。
特徴:
- 係数を0に近づけますが、完全に0にすることは稀です。
- そのため、モデルに含まれる変数の数は減りません。
- 相関の高い変数群がある場合、それらの係数を同じように縮小するため、多重共線性の問題に強いです。
Lasso回帰 (L1正則化)
Lasso(Least Absolute Shrinkage and Selection Operator)回帰は、損失関数に回帰係数の絶対値の和(L1ノルム)をペナルティ項として加えます。
目的関数: \[
\text{最小化する値} = \sum_{i=1}^{n}(y_i - \hat{y}_i)^2 + \lambda \sum_{j=1}^{p} |\beta_j|
\]
- ペナルティ項が係数の絶対値の和になっています。
特徴:
- 重要でないと判断された変数の係数を完全に0にすることができます。
- これにより、自動的に変数選択が行われ、モデルがシンプル(スパース)になります。
- 解釈しやすく、予測に本当に重要な変数が何かを知りたい場合に特に有用です。
ハイパーパラメータ \(\lambda\)
\(\lambda\) は正則化の強さを決めるパラメータです。
- \(\lambda = 0\) のとき、ペナルティはなくなり、通常の最小二乗法と同じになります。
- \(\lambda\) が大きいほどペナルティが強くなり、係数はより強く0に近づきます。 最適な \(\lambda\) の値は、交差検証(Cross-Validation)によってデータから決定するのが一般的です。
R言語によるシミュレーション
それでは、R言語を使ってシミュレーションを行い、Lasso回帰とRidge回帰の挙動を確認してみましょう。 ここでは、いくつかの変数は目的変数に影響を与え、多くの変数は影響を与えない(真の係数が0である)ようなデータを作成し、各手法がどのように係数を推定するかを比較します。
準備
まず、必要なライブラリを読み込みます。glmnetがLasso/Ridge回帰のためのパッケージです。
# ライブラリの読み込み
library(glmnet)
library(ggplot2)
library(dplyr)
library(tidyr)
library(broom)
seed <- 20250708ステップ1: サンプルデータの作成
目的変数に影響を与える変数が5つ、影響を与えない無関係な変数が15つある、合計20個の説明変数を持つデータセットを生成します。
# 再現性のためのシード設定
set.seed(seed)
n <- 100 # サンプルサイズ
p <- 20 # 説明変数の数
# 真の係数ベクトルを作成
# 最初の5つの変数のみが目的変数に影響し、残りの15個は影響しない(係数が0)
true_beta <- c(3, -2, 1.5, -1, 2.5, rep(0, p - 5))
# 説明変数Xを生成 (標準正規分布から)
X <- matrix(rnorm(n * p), nrow = n, ncol = p)
colnames(X) <- paste0("X", 1:p)
# 目的変数yを生成 (y = Xβ + ノイズ)
y <- X %*% true_beta + rnorm(n, mean = 0, sd = 2)ステップ2: モデルの学習と最適なλの選択
cv.glmnet()関数を使い、交差検証によって最適なλを求めながらモデルを学習させます。
alphaパラメータでモデルを指定します(alpha=1でLasso、alpha=0でRidge)。
# 交差検証によるLasso回帰の学習 (alpha = 1)
cv_lasso <- cv.glmnet(X, y, alpha = 1)
# 交差検証によるRidge回帰の学習 (alpha = 0)
cv_ridge <- cv.glmnet(X, y, alpha = 0)
# 最適なλ(予測誤差を最小にするλ)を取得
best_lambda_lasso <- cv_lasso$lambda.min
best_lambda_ridge <- cv_ridge$lambda.min
cat("Lassoの最適なλ (lambda.min):", best_lambda_lasso, ",log(λ) = ", log(best_lambda_lasso), " \n")
cat("Ridgeの最適なλ (lambda.min):", best_lambda_ridge, ",log(λ) = ", log(best_lambda_ridge), " \n")Lassoの最適なλ (lambda.min): 0.1246195 ,log(λ) = -2.08249
Ridgeの最適なλ (lambda.min): 0.2446332 ,log(λ) = -1.407995 ステップ3: 係数の比較
Lasso、Ridge、そして比較のための通常最小二乗法(OLS)で推定された係数を比較してみましょう。
# 各モデルの係数を取得
coef_lasso <- coef(cv_lasso, s = best_lambda_lasso)
coef_ridge <- coef(cv_ridge, s = best_lambda_ridge)
# 比較のために通常の最小二乗法(OLS)も実行
ols_model <- lm(y ~ X)
coef_ols <- coef(ols_model)
# 係数をデータフレームにまとめる
coef_df <- data.frame(
Variable = c("Intercept", paste0("X", 1:p)),
True = c(0, true_beta), # 切片の真値は0と仮定
OLS = as.vector(coef_ols),
Lasso = as.vector(coef_lasso),
Ridge = as.vector(coef_ridge)
) %>%
# 見やすいように小数点以下3桁に丸める
mutate(across(where(is.numeric), ~ round(., 3)))
# 結果の表示
cat("--- Lasso、Ridge、通常最小二乗法(OLS)で推定された係数の比較 ---\n")
print(coef_df)--- Lasso、Ridge、通常最小二乗法(OLS)で推定された係数の比較 ---
Variable True OLS Lasso Ridge
1 Intercept 0.0 -0.113 0.031 -0.044
2 X1 3.0 2.949 2.787 2.789
3 X2 -2.0 -2.330 -2.157 -2.187
4 X3 1.5 1.546 1.396 1.452
5 X4 -1.0 -1.156 -1.022 -1.113
6 X5 2.5 2.375 2.158 2.213
7 X6 0.0 0.071 0.000 0.061
8 X7 0.0 -0.024 0.000 -0.034
9 X8 0.0 0.331 0.326 0.338
10 X9 0.0 0.180 0.000 0.143
11 X10 0.0 0.223 0.082 0.184
12 X11 0.0 -0.184 -0.006 -0.145
13 X12 0.0 0.101 0.000 0.093
14 X13 0.0 -0.209 -0.161 -0.228
15 X14 0.0 -0.329 -0.166 -0.270
16 X15 0.0 0.211 0.035 0.178
17 X16 0.0 0.097 0.000 0.061
18 X17 0.0 -0.191 -0.095 -0.201
19 X18 0.0 0.062 0.046 0.104
20 X19 0.0 -0.296 -0.128 -0.277
21 X20 0.0 -0.121 0.000 -0.095結果の考察:
- OLS (最小二乗法): 真の係数が0である変数(X6~X20)に対しても、ノイズを拾ってしまい、0でない係数を推定しています。
- Lasso: 真の係数が0で
X6からX20の15の変数のうち、6つ変数(X6, X7, X9, X12, X16, X20)の係数を完全に0に推定できています。これはLassoの変数選択機能が働いていることを示しています。 - Ridge: 全ての変数の係数を0でない値として推定していますが、OLSと比較しますと X7, X13, X17, X18 の4つの変数以外は係数の絶対値が小さくなっています。これはRidgeの縮小効果を示しています。
ステップ4: 結果の可視化
結果をggplot2でプロットし、視覚的に理解を深めます。
係数比較プロット
各モデルが推定した係数を棒グラフで比較します。
# プロット用にデータを整形(縦長データに変換)
plot_data <- coef_df %>%
filter(Variable != "Intercept") %>% # 分析の主眼である説明変数の係数のみをプロット
pivot_longer(
cols = c(True, OLS, Lasso, Ridge),
names_to = "Model",
values_to = "Coefficient"
) %>%
# モデルの順序を整える
mutate(Model = factor(Model, levels = c("True", "OLS", "Lasso", "Ridge"))) %>%
# 変数の順序をX1, X2, ...の順にする
mutate(Variable = factor(Variable, levels = paste0("X", 1:p)))
# 棒グラフで係数を比較
ggplot(plot_data, aes(x = Variable, y = Coefficient, fill = Model)) +
geom_bar(stat = "identity", position = "dodge") +
labs(
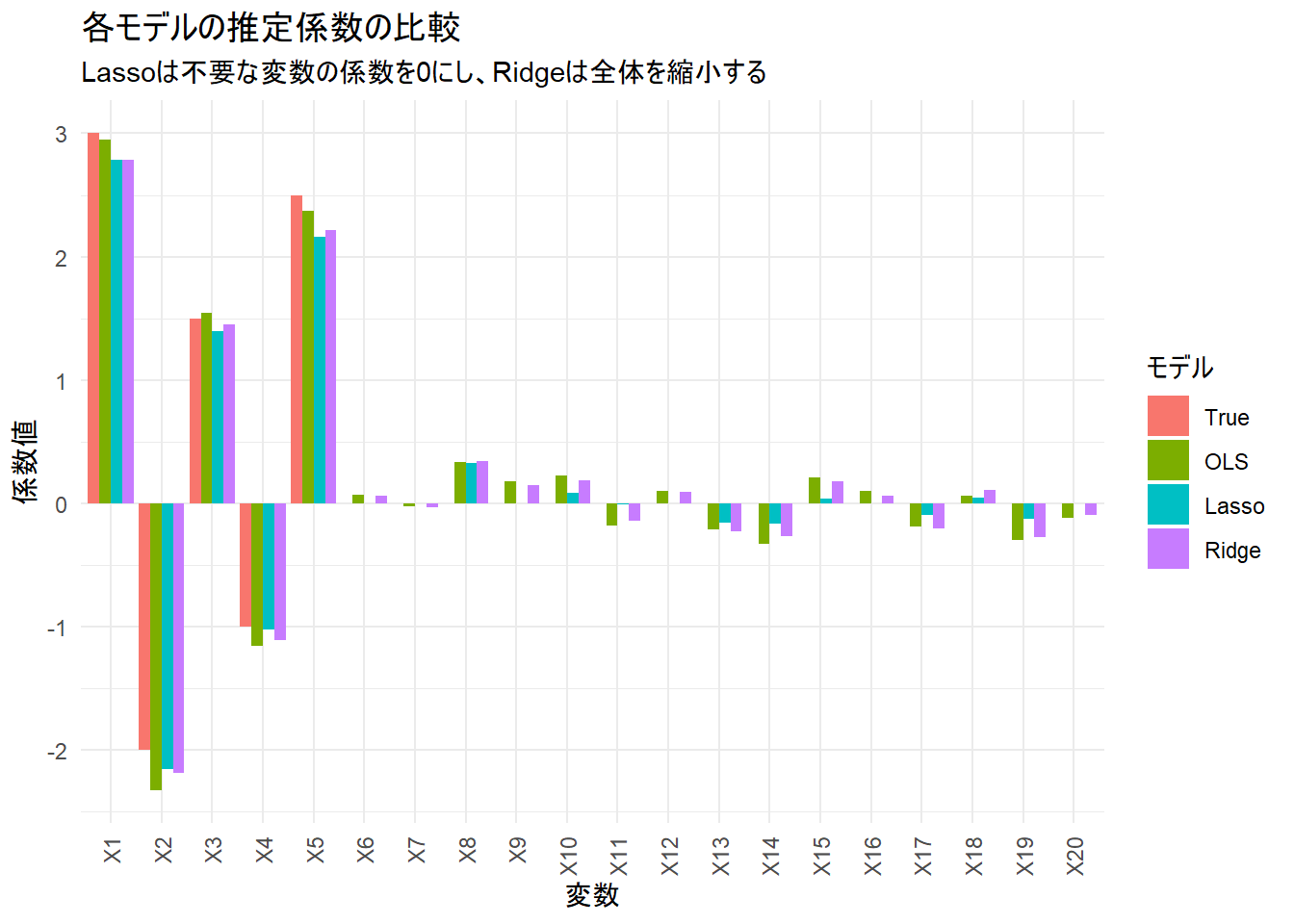
title = "各モデルの推定係数の比較",
subtitle = "Lassoは不要な変数の係数を0にし、Ridgeは全体を縮小する",
x = "変数",
y = "係数値",
fill = "モデル"
) +
theme_minimal() +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust = 1))Figure 1 から、以下が確認できます。
- True: 我々が設定した真の姿です。X1~X5のみが値を持ちます。
- OLS: 真の係数が0の変数(X6以降)にもバラついた値を持っています。
- Lasso: X6以降の6つ変数の係数が0になり、OLSと比較すると真のモデルに近くなっています。
- Ridge: 係数が0になることはありませんが、OLSに比べて全体的に係数が0の方向に縮小されています。
係数の軌跡プロット (Coefficient Path)
ハイパーパラメータλを変化させたときに、各変数の係数がどのように変わっていくかをプロットします。これはLassoとRidgeの本質的な違いを理解するのに役立ちます。
# glmnetモデルオブジェクトをbroom::tidyで整形
tidy_lasso <- broom::tidy(cv_lasso$glmnet.fit) %>% filter(term != "(Intercept)")
tidy_ridge <- broom::tidy(cv_ridge$glmnet.fit) %>% filter(term != "(Intercept)")
# LassoとRidgeのデータを結合
path_data <- bind_rows(
mutate(tidy_lasso, Model = "Lasso"),
mutate(tidy_ridge, Model = "Ridge")
)
# 交差検証で選ばれた最適なλを格納するデータフレームを作成
vline_data <- data.frame(
Model = c("Lasso", "Ridge"),
best_log_lambda = log(c(best_lambda_lasso, best_lambda_ridge))
)
path_data$term <- path_data$term %>% factor(levels = paste0("X", seq(p)))
# 軌跡プロットの作成(subtitleとgeom_vlineを修正)
ggplot(path_data, aes(x = log(lambda), y = estimate, group = term, color = term)) +
# 重要な変数(X1-X5)と不要な変数(X6-X20)で色分け
geom_line(data = . %>% filter(term %in% paste0("X", 1:5)), linewidth = 1.2) +
geom_line(data = . %>% filter(!term %in% paste0("X", 1:5)), linewidth = 0.5, linetype = "dashed") +
# ファセットごとに正しいλを描画するための専用データを指定
geom_vline(data = vline_data, aes(xintercept = best_log_lambda), linetype = "dotted", color = "red", linewidth = 1) +
facet_wrap(~Model, scales = "free_x") +
labs(
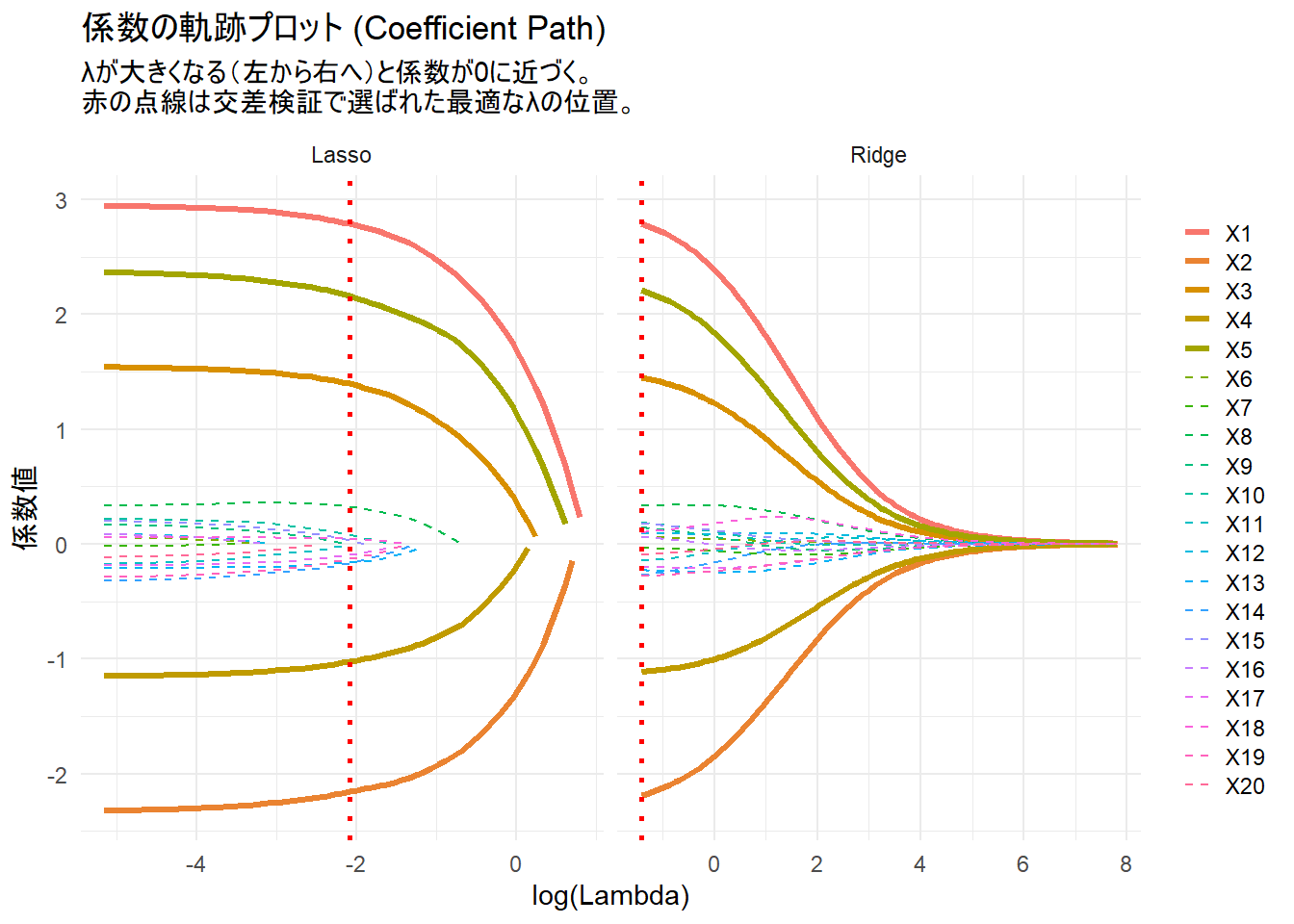
title = "係数の軌跡プロット (Coefficient Path)",
subtitle = "λが大きくなる(左から右へ)と係数が0に近づく。\n赤の点線は交差検証で選ばれた最適なλの位置。",
x = "log(Lambda)",
y = "係数値"
) +
theme_minimal() +
theme(
legend.spacing.y = unit(0.1, "cm"),
legend.key.size = unit(0.4, "cm"),
legend.title = element_blank()
)Figure 2 の見方:
- 横軸:
log(Lambda)です。左に行くほどλが小さく(ペナルティが弱く)、右に行くほどλが大きく(ペナルティが強く)なります。 - 縦軸: 係数の値です。
- Lasso: λが大きくなる(右へ移動する)につれて、多くの係数(破線)が次々と完全に0の線に到達しているのがわかります。これがLassoの変数選択です。
- Ridge: λが大きくなっても、係数は0に漸近しますが、完全に0にはなりません。すべての変数がモデルに残り続けます。
- 赤の点線: 交差検証で選ばれた最適なλの位置を示しています。この点で、モデルは未知のデータに対して最も良い予測性能を持つと期待されます。
以上です。