Rで サンプルサイズ設計:t検定(1群の平均値の検定) を確認します。
1. シミュレーションのシナリオ
シナリオ:ペットボトル飲料の内容量
ある飲料メーカーでは、主力商品である緑茶のペットボトルを「500ml」として販売しています。しかし、製造ラインのわずかなブレにより、実際の内容量にはばらつきが生じます。品質管理部門は、現在の製造ラインが正しく調整されているかを確認するため、定期的な抜き取り検査を行います。
- 検査の目的: 最近製造されたペットボトルの内容量の平均値が、規定値の 500ml と統計的に異なっていないかを確認する。もし有意に異なっていれば、製造ラインの再調整が必要となる。
- 検査対象: 製造ラインからランダムに抜き取られた緑茶のペットボトル。
サンプルサイズ設計のためのパラメータ設定:
- 有意水準 (α): 慣例に従い
0.05(両側検定)に設定します。内容量が多すぎても少なすぎても問題であるため、両側を考慮します。 - 検出力 (1 – β): もし内容量の平均が本当にずれているならば、その問題を90%という高い確率で検出したいので、
0.90に設定します。 - 効果量 (d):
- 基準値 (μ₀) は規定値の 500ml です。
- 過去のデータから、内容量の標準偏差 (σ) は 4ml であることが分かっています。
- 品質管理部門は、もし平均内容量が 2ml でもずれていれば(つまり498mlや502mlになっていれば)、それは製造ラインの調整が必要な重大な問題であると判断しました。これが検出したい平均値と基準値の差 (|μ – μ₀|) です。
- したがって、効果量
d = |μ - μ₀| / σ = 2 / 4 = 0.5(中程度の効果量)を確実に検出できるようにしたいと考えます。
このシナリオに基づき、「規定値から2mlのズレを90%の確率で検出するには、何本のペットボトルを抜き取り検査する必要があるか?」を計算し、シミュレーションで検証します。
各パラメータの意味
- 有意水準 (α, alpha)
- 帰無仮説(H₀: 標本群の母平均は基準値と等しい, μ = μ₀)が棄却されないにもかかわらず、それを棄却してしまう確率(第1種の過誤)。
- 一般的に
α = 0.05に設定されますが、目的により異なります。
- 検出力 (Power, 1 – β)
- 対立仮説(H₁: 標本群の母平均は基準値と異なる, μ ≠ μ₀)が真であるときに、その差を正しく検出できる確率。
βは第2種の過誤(差があることを見逃す確率)です。 - 一般的に
1 - β = 0.80や0.90に設定されますが、目的により異なります。
- 対立仮説(H₁: 標本群の母平均は基準値と異なる, μ ≠ μ₀)が真であるときに、その差を正しく検出できる確率。
- 効果量 (Effect Size, d)
- 検出したい「母平均と基準値との差」の大きさを、標準偏差で標準化した指標です。Cohen’s dが用いられます。
-
d = |μ - μ₀| / σ-
μ: 検出したい真の母平均。 -
μ₀: 比較対象となる基準値。 -
σ: 母集団の標準偏差。
-
- 効果量の大きさは、その分野で意味のある差や過去の研究に基づいて決定します。
- サンプルサイズ (n)
- 研究に必要なサンプルの数。これを求めます。
2. R言語によるシミュレーションコード
まず、必要なライブラリを読み込みます。
library(pwr)
library(ggplot2)
library(dplyr)
seed <- 20250708ステップ1: シナリオに基づいたサンプルサイズの計算
Rのpwrパッケージにあるpwr.t.test関数で、type = "one.sample"を指定して計算します。
cat("--- ステップ1: サンプルサイズの計算 ---\n")
# パラメータ設定
effect_size <- 0.5 # Cohen's d
sig_level <- 0.05 # 有意水準 alpha
power_level <- 0.90 # 検出力 1-beta
# サンプルサイズの計算
# nをNULLにすることで、必要なサンプルサイズを計算させる
sample_size_calc <- pwr.t.test(
d = effect_size,
sig.level = sig_level,
power = power_level,
type = "one.sample", # 1群のt検定
alternative = "two.sided" # 両側検定
)
# 結果の表示
print(sample_size_calc)
# 必要なサンプルサイズ(ペットボトルの本数)を取得(切り上げ)
n_required <- ceiling(sample_size_calc$n)
cat(paste0("\n結論: この検査には最低 ", n_required, " 本のペットボトルが必要です。\n"))--- ステップ1: サンプルサイズの計算 ---
One-sample t test power calculation
n = 43.99548
d = 0.5
sig.level = 0.05
power = 0.9
alternative = two.sided
結論: この検査には最低 44 本のペットボトルが必要です。計算結果から、この検査には44本のペットボトルが必要であることがわかります。
ステップ2: 検出力のシミュレーション (対立仮説が真の場合)
計算で得られたサンプルサイズ(44本)を用いて、本当に検出力が90%程度になるかシミュレーションで確認します。
cat("--- ステップ2: 検出力のシミュレーション ---\n")
# シミュレーションのパラメータ設定
set.seed(seed) # 結果を再現可能にする
n_sim <- 10000 # シミュレーション回数
# シナリオの母集団パラメータ
mu_0 <- 500 # 基準値 (ml)
sd_val <- 4 # 標準偏差 (ml)
# 対立仮説が真である場合の平均値(2mlずれている)
mu_1 <- mu_0 - (effect_size * sd_val) # 498mlを想定
# 結果を格納するベクトル
p_values_h1 <- numeric(n_sim)
# シミュレーションループ
for (i in 1:n_sim) {
# 1. 対立仮説が真である状況のデータを生成
sample_data <- rnorm(n = n_required, mean = mu_1, sd = sd_val)
# 2. 1群のt検定を実行
t_test_result <- t.test(sample_data, mu = mu_0)
# 3. p値を保存
p_values_h1[i] <- t_test_result$p.value
}
# シミュレーションによる検出力の計算
simulated_power <- mean(p_values_h1 < sig_level)
cat(paste0("\nシミュレーションによる検出力: ", round(simulated_power, 3), "\n"))--- ステップ2: 検出力のシミュレーション ---
シミュレーションによる検出力: 0.903シミュレーション結果は、目標とした検出力0.90に近い値(約0.903)となり、サンプルサイズ設計の妥当性が裏付けられました。
ステップ3: 検出力シミュレーション結果の可視化
cat("--- ステップ3: 検出力シミュレーション結果の可視化 ---\n")
p_values_df_h1 <- data.frame(p_value = p_values_h1)
plot_power <- ggplot(p_values_df_h1, aes(x = p_value)) +
geom_histogram(binwidth = 0.05, fill = "skyblue", color = "black", boundary = 0) +
geom_vline(xintercept = sig_level, color = "red", linetype = "dashed", linewidth = 1) +
annotate("text",
x = 0.5, y = 5000,
label = paste("シミュレーションによる検出力 (p < 0.05) =", round(simulated_power, 3)),
color = "red", size = 5
) +
labs(
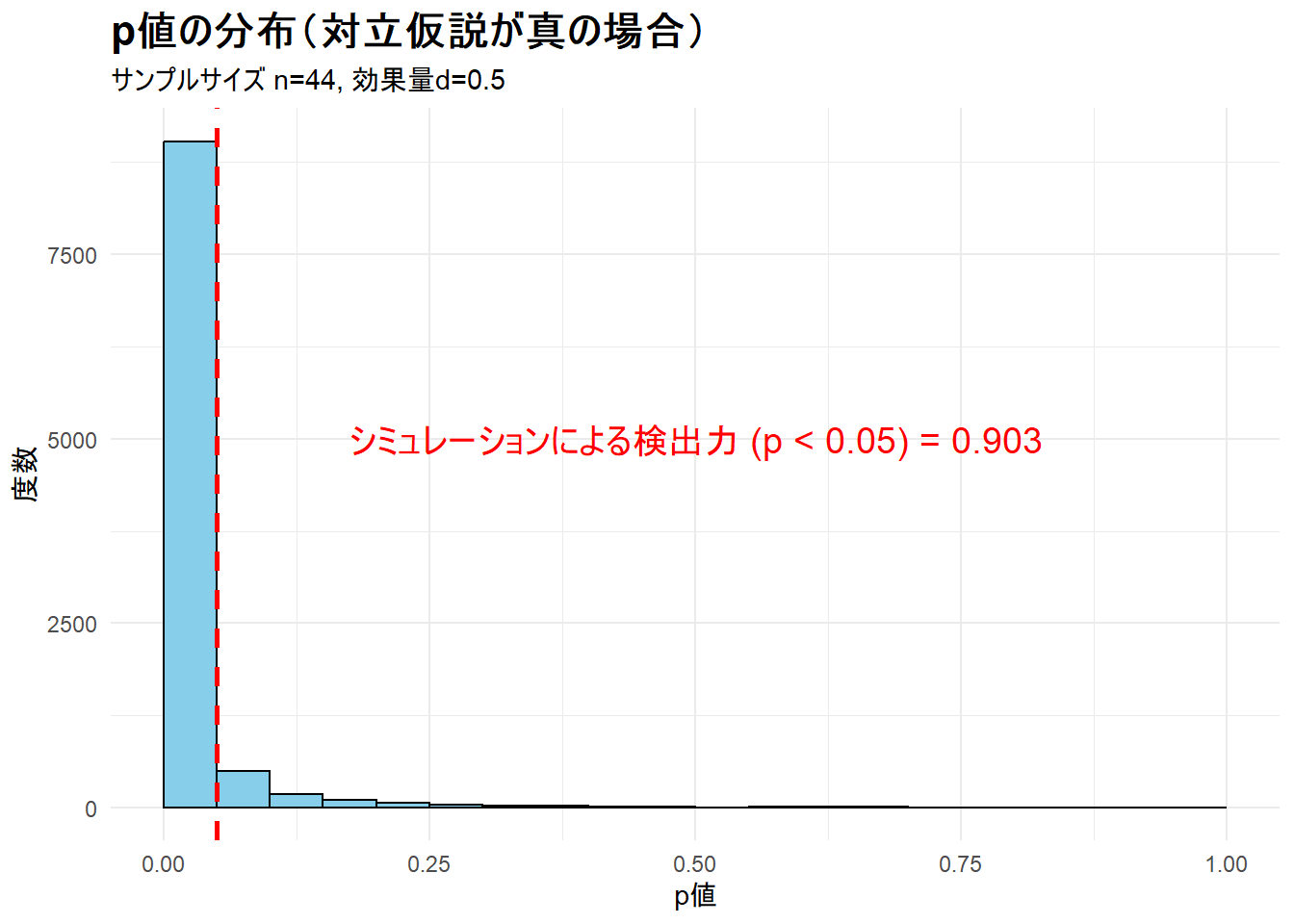
title = "p値の分布(対立仮説が真の場合)",
subtitle = paste0("サンプルサイズ n=", n_required, ", 効果量d=", effect_size),
x = "p値",
y = "度数"
) +
theme_minimal() +
theme(plot.title = element_text(size = 16, face = "bold"))
print(plot_power)--- ステップ3: 検出力シミュレーション結果の可視化 ---Figure 1 では、p値が0に近い方に強く偏っており、これは平均値のズレを正しく検出できていることを示唆しています。
ステップ4: 第1種の過誤のシミュレーション (帰無仮説が棄却されない場合)
次に、製造ラインが完璧に調整されていて内容量の平均が500mlである場合(帰無仮説が棄却されない場合)に、誤って「ズレている」と結論づけてしまう確率(第1種の過誤率)が、設定した有意水準α (0.05)と一致するかを確認します。
cat("--- ステップ4: 第1種の過誤のシミュレーション ---\n")
p_values_h0 <- numeric(n_sim)
for (i in 1:n_sim) {
# 1. 帰無仮説が棄却されない状況のデータを生成 (平均は基準値と同じ500ml)
sample_data_h0 <- rnorm(n = n_required, mean = mu_0, sd = sd_val)
# 2. 1群のt検定を実行
t_test_result_h0 <- t.test(sample_data_h0, mu = mu_0)
# 3. p値を保存
p_values_h0[i] <- t_test_result_h0$p.value
}
type1_error_rate <- mean(p_values_h0 < sig_level)
cat(paste("\nシミュレーションによる第1種の過誤率:", round(type1_error_rate, 3), "\n"))--- ステップ4: 第1種の過誤のシミュレーション ---
シミュレーションによる第1種の過誤率: 0.046 シミュレーションによる第1種の過誤率は、設定した有意水準0.05に近い値(約0.046)となり、検定が正しく機能していることがわかります。
ステップ5: 第1種の過誤シミュレーション結果の可視化
cat("--- ステップ5: 第1種の過誤シミュレーション結果の可視化 ---\n")
p_values_df_h0 <- data.frame(p_value = p_values_h0)
expected_freq <- n_sim * 0.05
plot_alpha <- ggplot(p_values_df_h0, aes(x = p_value)) +
geom_histogram(binwidth = 0.05, fill = "lightcoral", color = "black", boundary = 0) +
geom_vline(xintercept = sig_level, color = "blue", linetype = "dashed", linewidth = 1) +
geom_hline(yintercept = expected_freq, color = "darkgreen", linetype = "dotted", linewidth = 1) +
annotate("text",
x = 0.5, y = 600,
label = paste("第1種の過誤の確率 (p < 0.05) =", round(type1_error_rate, 3)),
color = "blue", size = 5
) +
labs(
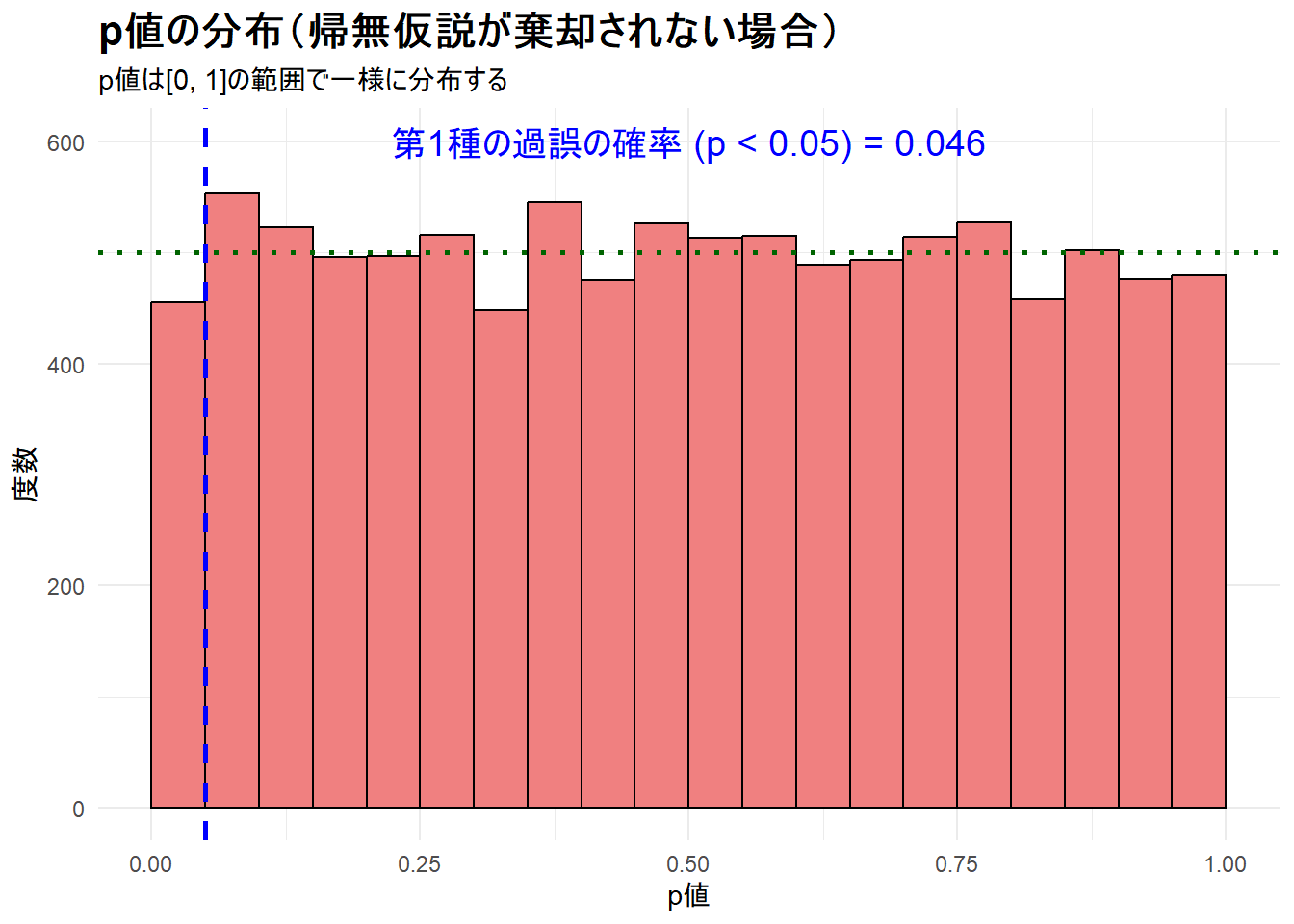
title = "p値の分布(帰無仮説が棄却されない場合)",
subtitle = "p値は[0, 1]の範囲で一様に分布する",
x = "p値",
y = "度数"
) +
theme_minimal() +
theme(plot.title = element_text(size = 16, face = "bold"))
print(plot_alpha)--- ステップ5: 第1種の過誤シミュレーション結果の可視化 ---Figure 2 は、p値がほぼフラットな分布を示しており、これにより、偶然だけで有意な差が出る確率が、意図通り5%にコントロールされていることが視覚的に確認できます。
以上です。