Rで 二分法 を試みます。
1. 二分法とは
二分法(Bisection Method)は、方程式 f(x) = 0 の解(根)を数値的に求めるための、最も基本的なアルゴリズムの一つです。この方法は中間値の定理に基づいています。
中間値の定理とは?
関数
f(x)が閉区間[a, b]で連続であり、f(a)とf(b)の値が異なるとき、f(a)とf(b)の間の任意の値kに対して、f(c) = kとなるcがaとbの間に少なくとも一つ存在する。
二分法では、この定理を k=0 の場合に適用します。つまり、f(a) と f(b) の符号が異なる(一方が正で、もう一方が負)ならば、f(c) = 0 となる c(すなわち方程式の解)が区間 (a, b) の中に必ず存在すると言えます。
アルゴリズムの手順
二分法は、解が存在する区間 [a, b] の幅を繰り返し半分に狭めていくことで、解に近づいていきます。
- 初期設定:
- 解を求めたい関数
f(x)を定義します。 - 解が存在するであろう区間
[a, b]を設定します。このとき、f(a) * f(b) < 0(f(a)とf(b)の符号が異なる)という条件を満たす必要があります。 - 計算を終了するための許容誤差
tol(tolerance) と、最大反復回数max_iterを決めます。
- 解を求めたい関数
- 反復計算: 以下の処理を、区間の幅
b - aが許容誤差tolより小さくなるか、最大反復回数に達するまで繰り返します。- 区間
[a, b]の 中点cを計算します。c = (a + b) / 2 - 中点
cにおける関数値f(c)を計算します。 -
f(c)の符号を調べ、解が存在する新しい区間を決定します。- もし
f(c)がf(a)と同じ符号なら、解は[c, b]の間にあります。そこで、次のステップのためにaをcに更新します (a = c)。 - もし
f(c)がf(b)と同じ符号なら、解は[a, c]の間にあります。そこで、次のステップのためにbをcに更新します (b = c)。 - もし
f(c) = 0なら、cが厳密な解なので計算を終了します。
- もし
- 区間
- 終了:
- ループが終了した時点での中点
cを、方程式f(x) = 0の近似解とします。
- ループが終了した時点での中点
特徴
- 長所: 初期区間に解が一つ存在すれば、アルゴリズムは必ず解に収束します。非常に頑健な方法です。
- 短所: 収束の速さが比較的遅い(線形収束)ため、高精度な解を得るためには反復回数が多くなることがあります。
2. R言語によるシミュレーションコードと実行結果
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
# -----------------------------------------------------------------
# 1. シミュレーションの対象となる関数を定義
# -----------------------------------------------------------------
# f(x) = x^3 - x - 1
f <- function(x) {
return(x^3 - x - 1)
}
# -----------------------------------------------------------------
# 2. 二分法のシミュレーションを行う関数を定義
# -----------------------------------------------------------------
bisection_simulation <- function(func, a, b, tol = 1e-6, max_iter = 20) {
# f(a)とf(b)の符号が同じ場合はエラー
if (func(a) * func(b) >= 0) {
stop("初期区間[a, b]でf(a)とf(b)の符号が同じです。異なる符号になるように設定してください。")
}
cat("--- 二分法シミュレーション開始 ---\n\n")
cat(sprintf("対象関数: x^3 - x - 1\n"))
cat(sprintf("初期区間: [%.1f, %.1f]\n", a, b))
cat(sprintf("許容誤差: %e\n\n", tol))
# 各ステップの結果を保存するためのデータフレームを初期化
history <- data.frame(
iter = integer(),
a = double(),
b = double(),
c = double(),
fa = double(),
fb = double(),
fc = double(),
width = double()
)
# 反復計算
for (i in 1:max_iter) {
c <- (a + b) / 2 # 中点を計算
fa <- func(a)
fb <- func(b)
fc <- func(c)
# 現在のステップの情報をデータフレームに追加
history <- rbind(history, data.frame(
iter = i, a = a, b = b, c = c,
fa = fa, fb = fb, fc = fc, width = b - a
))
# 現在の状態を出力
cat(sprintf("【反復 %d回目】\n", i))
cat(sprintf(" 区間 = [%.6f, %.6f], 区間の幅 = %.6f\n", a, b, b - a))
cat(sprintf(" 中点 c = %.6f\n", c))
cat(sprintf(" f(a) = %.6f, f(c) = %.6f\n", fa, fc))
# 収束判定
if ((b - a) / 2 < tol || fc == 0) {
cat("\n--- 収束しました ---\n\n")
break
}
# 区間の更新
if (fa * fc < 0) {
b <- c # 解は [a, c] にある
cat(" f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。\n\n")
} else {
a <- c # 解は [c, b] にある
cat(" f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。\n\n")
}
}
if (i == max_iter && (b - a) / 2 >= tol) {
cat("\n--- 最大反復回数に達しました ---\n")
}
cat(sprintf("最終的な解の近似値 c = %.6f\n", c))
cat(sprintf("そのときの関数値 f(c) = %e\n", fc))
return(history)
}
# -----------------------------------------------------------------
# 3. シミュレーションの実行
# -----------------------------------------------------------------
# 初期値を設定
a_init <- 1.0
b_init <- 2.0
tolerance <- 1e-5
# シミュレーションを実行し、計算過程のデータを取得
simulation_history <- bisection_simulation(f, a_init, b_init, tol = tolerance)
# -----------------------------------------------------------------
# 4. ggplot2による結果の可視化
# -----------------------------------------------------------------
# 関数の曲線を描画するためのデータを作成
curve_data <- data.frame(x = seq(0.8, 2.2, length.out = 200)) %>%
mutate(y = f(x))
# 最終的な解
final_solution <- tail(simulation_history, 1)
# プロットを作成
bisection_plot <- ggplot() +
# y=0 の線 (解の目標)
geom_hline(yintercept = 0, linetype = "dashed", color = "gray50") +
# f(x)のグラフ
geom_line(data = curve_data, aes(x = x, y = y), color = "blue", linewidth = 0.1) +
# 各反復ステップでの中点 (c, f(c)) をプロット
geom_point(data = simulation_history, aes(x = c, y = fc, color = iter), size = 3.0) +
# 各反復ステップでの探索区間 [a, b] をy軸の下部に表示
geom_segment(
data = simulation_history,
aes(x = a, xend = b, y = -1.5 - iter * 0.4, yend = -1.5 - iter * 0.4, color = iter),
linewidth = 1.5
) +
# テキストをセグメントの右横に表示
geom_text(
data = simulation_history,
aes(x = b + 0.02, y = -1.5 - iter * 0.4, label = paste0(iter, " 回目")),
size = 3, hjust = 0, vjust = 0.5, color = "black"
) +
# 最終的な解を点とテキストで強調
geom_point(data = final_solution, aes(x = c, y = 0), size = 5, shape = 8, color = "red") +
geom_text(
data = final_solution,
aes(x = c, y = 0.5, label = sprintf("近似解\nx = %.5f", c)),
color = "red", hjust = 0, vjust = 0
) +
# スケールとラベルの設定
scale_color_gradient(low = "lightblue", high = "darkred") +
coord_cartesian(ylim = c(-9, 6)) +
labs(
title = "二分法による方程式 f(x) = x^3 - x - 1 の求解プロセス",
subtitle = "区間が徐々に狭まり、解に収束していく様子",
x = "x",
y = "f(x)"
) +
theme_minimal(base_family = "sans") +
theme(
plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5),
legend.position = "none"
)
# プロットを表示
print(bisection_plot)--- 二分法シミュレーション開始 ---
対象関数: x^3 - x - 1
初期区間: [1.0, 2.0]
許容誤差: 1.000000e-05
【反復 1回目】
区間 = [1.000000, 2.000000], 区間の幅 = 1.000000
中点 c = 1.500000
f(a) = -1.000000, f(c) = 0.875000
f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。
【反復 2回目】
区間 = [1.000000, 1.500000], 区間の幅 = 0.500000
中点 c = 1.250000
f(a) = -1.000000, f(c) = -0.296875
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 3回目】
区間 = [1.250000, 1.500000], 区間の幅 = 0.250000
中点 c = 1.375000
f(a) = -0.296875, f(c) = 0.224609
f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。
【反復 4回目】
区間 = [1.250000, 1.375000], 区間の幅 = 0.125000
中点 c = 1.312500
f(a) = -0.296875, f(c) = -0.051514
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 5回目】
区間 = [1.312500, 1.375000], 区間の幅 = 0.062500
中点 c = 1.343750
f(a) = -0.051514, f(c) = 0.082611
f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。
【反復 6回目】
区間 = [1.312500, 1.343750], 区間の幅 = 0.031250
中点 c = 1.328125
f(a) = -0.051514, f(c) = 0.014576
f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。
【反復 7回目】
区間 = [1.312500, 1.328125], 区間の幅 = 0.015625
中点 c = 1.320312
f(a) = -0.051514, f(c) = -0.018711
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 8回目】
区間 = [1.320312, 1.328125], 区間の幅 = 0.007812
中点 c = 1.324219
f(a) = -0.018711, f(c) = -0.002128
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 9回目】
区間 = [1.324219, 1.328125], 区間の幅 = 0.003906
中点 c = 1.326172
f(a) = -0.002128, f(c) = 0.006209
f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。
【反復 10回目】
区間 = [1.324219, 1.326172], 区間の幅 = 0.001953
中点 c = 1.325195
f(a) = -0.002128, f(c) = 0.002037
f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。
【反復 11回目】
区間 = [1.324219, 1.325195], 区間の幅 = 0.000977
中点 c = 1.324707
f(a) = -0.002128, f(c) = -0.000047
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 12回目】
区間 = [1.324707, 1.325195], 区間の幅 = 0.000488
中点 c = 1.324951
f(a) = -0.000047, f(c) = 0.000995
f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。
【反復 13回目】
区間 = [1.324707, 1.324951], 区間の幅 = 0.000244
中点 c = 1.324829
f(a) = -0.000047, f(c) = 0.000474
f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。
【反復 14回目】
区間 = [1.324707, 1.324829], 区間の幅 = 0.000122
中点 c = 1.324768
f(a) = -0.000047, f(c) = 0.000214
f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。
【反復 15回目】
区間 = [1.324707, 1.324768], 区間の幅 = 0.000061
中点 c = 1.324738
f(a) = -0.000047, f(c) = 0.000084
f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。
【反復 16回目】
区間 = [1.324707, 1.324738], 区間の幅 = 0.000031
中点 c = 1.324722
f(a) = -0.000047, f(c) = 0.000018
f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。
【反復 17回目】
区間 = [1.324707, 1.324722], 区間の幅 = 0.000015
中点 c = 1.324715
f(a) = -0.000047, f(c) = -0.000014
--- 収束しました ---
最終的な解の近似値 c = 1.324715
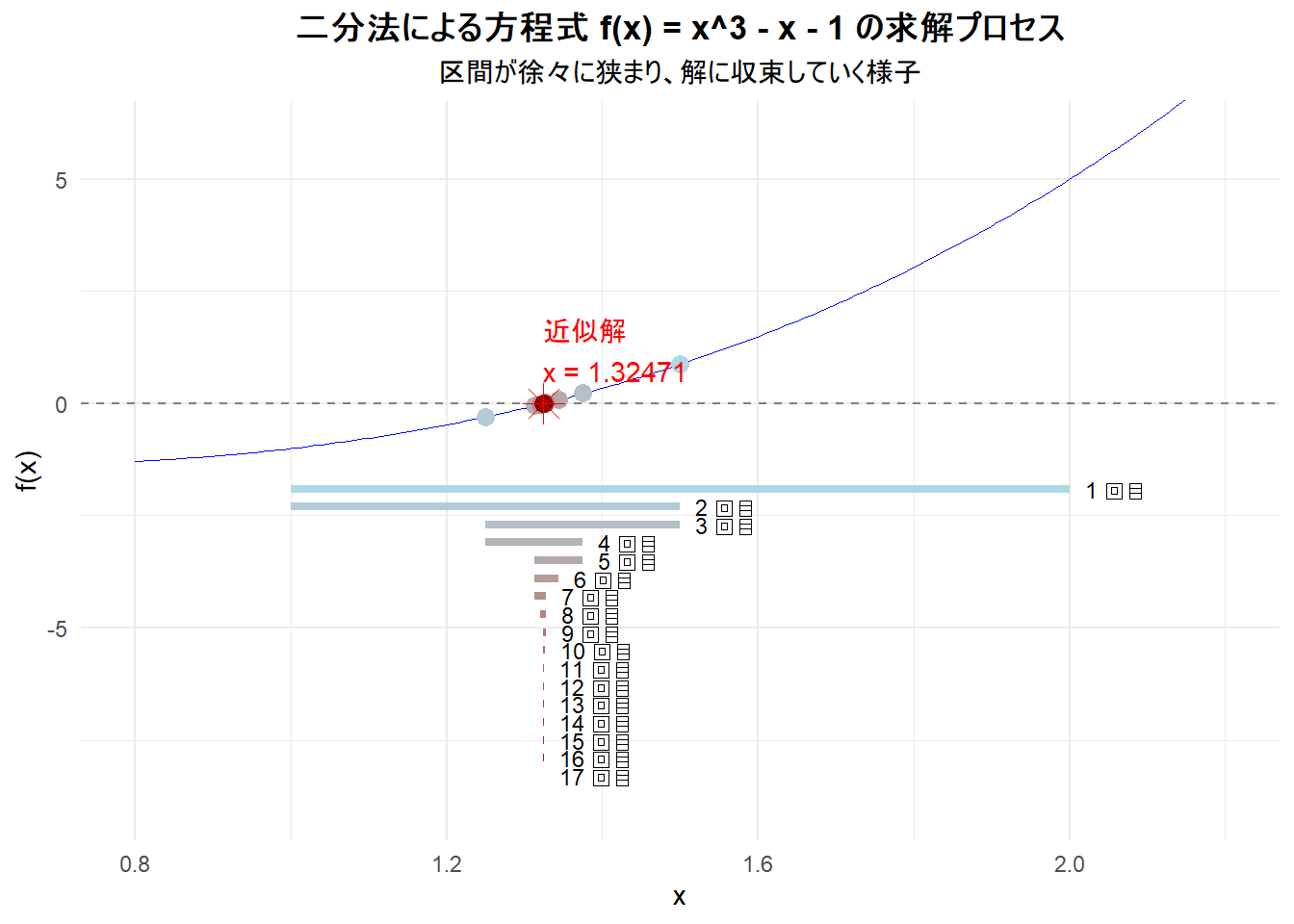
そのときの関数値 f(c) = -1.405875e-05Figure 1 の読み方
- 青い曲線: 対象としている関数
f(x) = x^3 - x - 1のグラフです。 - 灰色の破線:
y=0のラインです。この線と青い曲線が交わる点が、求めたい解です。 - 色のついた点: 各反復計算で評価された中点
cとその関数値f(c)を示しています。色は反復回数を表し、水色(初期)から赤色(終盤)に変化します。 - グラフ下部の線分: 各反復回数における探索区間
[a, b]を示しています。回数を重ねるごとに、区間の幅が半分になり、急速に狭まっていく様子がわかります。 - 赤い星印: 最終的に得られた近似解の位置を示しています。
以上です。