Rで はさみうち法 を試みます。
本ポストはこちらの続きです。

1. はさみうち法とは
はさみうち法(False Position Method または Regula Falsi)は、二分法と同じく方程式 f(x) = 0 の解を区間で挟みながら探索するアルゴリズムです。二分法と同様に中間値の定理を基礎としており、f(a) と f(b) の符号が異なる初期区間 [a, b] が必要です。
二分法との違い
二分法が常に区間の機械的な中点 (a+b)/2 を次の探索点とするのに対し、はさみうち法は、区間の両端の点 (a, f(a)) と (b, f(b)) を結ぶ直線(弦)を考えます。そして、この直線がx軸と交わる点を次の近似解 c とします。
関数のグラフが直線に近い形をしていれば、この交点 c は実際の方程式の解に非常に近くなることが期待できます。これにより、二分法よりも速く解に収束する場合があります。
アルゴリズムの手順
- 初期設定:
- 二分法と同様に、関数
f(x)、f(a) * f(b) < 0を満たす初期区間[a, b]、許容誤差tol、最大反復回数max_iterを設定します。
- 二分法と同様に、関数
- 反復計算: 以下の処理を、
|f(c)|が許容誤差tolより小さくなるか、最大反復回数に達するまで繰り返します。区間の両端
(a, f(a))と(b, f(b))を結ぶ直線がx軸と交わる点cを計算します。このcは以下の式で求められます。c = (a * f(b) - b * f(a)) / (f(b) - f(a))中点
cにおける関数値f(c)を計算します。f(c)の符号を調べ、解が存在する新しい区間を決定します。(この部分は二分法と全く同じです)- もし
f(a)とf(c)の符号が異なるなら、解は[a, c]の間にあるため、bをcに更新します (b = c)。 - もし
f(a)とf(c)の符号が同じなら、解は[c, b]の間にあるため、aをcに更新します (a = c)。
- もし
- 終了:
- ループが終了した時点での
cを、方程式f(x) = 0の近似解とします。
- ループが終了した時点での
特徴
- 長所: 多くの場合、二分法よりも収束が速い(超線形収束)。
- 短所: 関数の形状(グラフの凹凸)によっては、区間の一方の端点が全く更新されず、収束が著しく遅くなることがあります。今回のシミュレーションでもその様子が観察できます。
2. R言語によるシミュレーションコードと実行結果
それでは、二分法と同じ方程式 f(x) = x^3 - x - 1 = 0 を例に、はさみうち法のシミュレーションを行います。初期区間も同じ [1, 2] です。
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
# -----------------------------------------------------------------
# 1. シミュレーションの対象となる関数を定義 (二分法と同じ)
# -----------------------------------------------------------------
# f(x) = x^3 - x - 1
f <- function(x) {
return(x^3 - x - 1)
}
# -----------------------------------------------------------------
# 2. はさみうち法のシミュレーションを行う関数を定義
# -----------------------------------------------------------------
false_position_simulation <- function(func, a, b, tol = 1e-6, max_iter = 20) {
if (func(a) * func(b) >= 0) {
stop("初期区間[a, b]でf(a)とf(b)の符号が同じです。異なる符号になるように設定してください。")
}
cat("--- はさみうち法シミュレーション開始 ---\n\n")
cat(sprintf("対象関数: x^3 - x - 1\n"))
cat(sprintf("初期区間: [%.1f, %.1f]\n", a, b))
cat(sprintf("許容誤差: %e\n\n", tol))
history <- data.frame(
iter = integer(),
a = double(),
b = double(),
c = double(),
fa = double(),
fb = double(),
fc = double()
)
# 反復計算
for (i in 1:max_iter) {
fa <- func(a)
fb <- func(b)
# 次の近似解cを計算 (はさみうち法の核)
c <- (a * fb - b * fa) / (fb - fa)
fc <- func(c)
history <- rbind(history, data.frame(
iter = i, a = a, b = b, c = c,
fa = fa, fb = fb, fc = fc
))
cat(sprintf("【反復 %d回目】\n", i))
cat(sprintf(" 区間 = [%.6f, %.6f]\n", a, b))
cat(sprintf(" 次の点 c = %.6f\n", c))
cat(sprintf(" f(a) = %.6f, f(c) = %.6f\n", fa, fc))
# 収束判定
if (abs(fc) < tol) {
cat("\n--- 収束しました ---\n\n")
break
}
# 区間の更新
if (fa * fc < 0) {
b <- c
cat(" f(a)とf(c)の符号が異なるため、次の区間は [a, c] になります。\n\n")
} else {
a <- c
cat(" f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。\n\n")
}
}
if (i == max_iter && abs(fc) >= tol) {
cat("\n--- 最大反復回数に達しました ---\n")
}
cat(sprintf("最終的な解の近似値 c = %.6f\n", c))
cat(sprintf("そのときの関数値 f(c) = %e\n", fc))
return(history)
}
# -----------------------------------------------------------------
# 3. シミュレーションの実行
# -----------------------------------------------------------------
# 初期値を設定
a_init <- 1.0
b_init <- 2.0
tolerance <- 1e-5
# シミュレーションを実行
simulation_history_fp <- false_position_simulation(f, a_init, b_init, tol = tolerance)
# -----------------------------------------------------------------
# 4. ggplot2による結果の可視化
# -----------------------------------------------------------------
# 関数の曲線を描画するためのデータ
curve_data <- data.frame(x = seq(0.8, 2.2, length.out = 200)) %>%
mutate(y = f(x))
# 最終的な解
final_solution_fp <- tail(simulation_history_fp, 1)
# プロットを作成
false_position_plot <- ggplot() +
# y=0 の線
geom_hline(yintercept = 0, linetype = "dashed", color = "gray50") +
# 各反復ステップでの弦 (a,f(a))-(b,f(b)) を描画
geom_segment(
data = simulation_history_fp,
aes(x = a, y = fa, xend = b, yend = fb, color = iter),
linetype = "dotted", linewidth = 0.8
) +
# f(x)のグラフ
geom_line(data = curve_data, aes(x = x, y = y), color = "blue", linewidth = 1.2) +
# 各反復ステップで計算された点 c をx軸上にプロット
geom_point(data = simulation_history_fp, aes(x = c, y = 0, color = iter), size = 3) +
# 最終的な解を強調
geom_point(data = final_solution_fp, aes(x = c, y = 0), size = 5, shape = 8, color = "red") +
geom_text(
data = final_solution_fp,
aes(x = c, y = 0.5, label = sprintf("近似解\nx = %.5f", c)),
color = "red", hjust = 0, vjust = 0
) +
# スケールとラベルの設定
scale_color_gradient(low = "lightblue", high = "darkred") +
labs(
title = "はさみうち法による方程式 f(x) = x^3 - x - 1 の求解プロセス",
subtitle = "弦とx軸の交点を次の探索点とし、解に収束していく様子",
x = "x",
y = "f(x)"
) +
theme_minimal(base_family = "sans") +
theme(
plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5),
legend.position = "none" # 凡例は非表示
)
# プロットを表示
print(false_position_plot)--- はさみうち法シミュレーション開始 ---
対象関数: x^3 - x - 1
初期区間: [1.0, 2.0]
許容誤差: 1.000000e-05
【反復 1回目】
区間 = [1.000000, 2.000000]
次の点 c = 1.166667
f(a) = -1.000000, f(c) = -0.578704
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 2回目】
区間 = [1.166667, 2.000000]
次の点 c = 1.253112
f(a) = -0.578704, f(c) = -0.285363
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 3回目】
区間 = [1.253112, 2.000000]
次の点 c = 1.293437
f(a) = -0.285363, f(c) = -0.129542
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 4回目】
区間 = [1.293437, 2.000000]
次の点 c = 1.311281
f(a) = -0.129542, f(c) = -0.056588
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 5回目】
区間 = [1.311281, 2.000000]
次の点 c = 1.318989
f(a) = -0.056588, f(c) = -0.024304
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 6回目】
区間 = [1.318989, 2.000000]
次の点 c = 1.322283
f(a) = -0.024304, f(c) = -0.010362
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 7回目】
区間 = [1.322283, 2.000000]
次の点 c = 1.323684
f(a) = -0.010362, f(c) = -0.004404
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 8回目】
区間 = [1.323684, 2.000000]
次の点 c = 1.324279
f(a) = -0.004404, f(c) = -0.001869
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 9回目】
区間 = [1.324279, 2.000000]
次の点 c = 1.324532
f(a) = -0.001869, f(c) = -0.000793
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 10回目】
区間 = [1.324532, 2.000000]
次の点 c = 1.324639
f(a) = -0.000793, f(c) = -0.000336
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 11回目】
区間 = [1.324639, 2.000000]
次の点 c = 1.324685
f(a) = -0.000336, f(c) = -0.000143
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 12回目】
区間 = [1.324685, 2.000000]
次の点 c = 1.324704
f(a) = -0.000143, f(c) = -0.000060
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 13回目】
区間 = [1.324704, 2.000000]
次の点 c = 1.324712
f(a) = -0.000060, f(c) = -0.000026
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 14回目】
区間 = [1.324712, 2.000000]
次の点 c = 1.324715
f(a) = -0.000026, f(c) = -0.000011
f(a)とf(c)の符号が同じため、次の区間は [c, b] になります。
【反復 15回目】
区間 = [1.324715, 2.000000]
次の点 c = 1.324717
f(a) = -0.000011, f(c) = -0.000005
--- 収束しました ---
最終的な解の近似値 c = 1.324717
そのときの関数値 f(c) = -4.610916e-06注目点: 二分法では許容誤差
1e-5に到達するのに17回かかりましたが、はさみうち法では15回で収束しています。また、区間[a, b]の右端b=2.0が一度も更新されず、左端aだけが更新され続けていることがわかります。これは、この関数の形状(下に凸)による典型的なはさみうち法の挙動です。
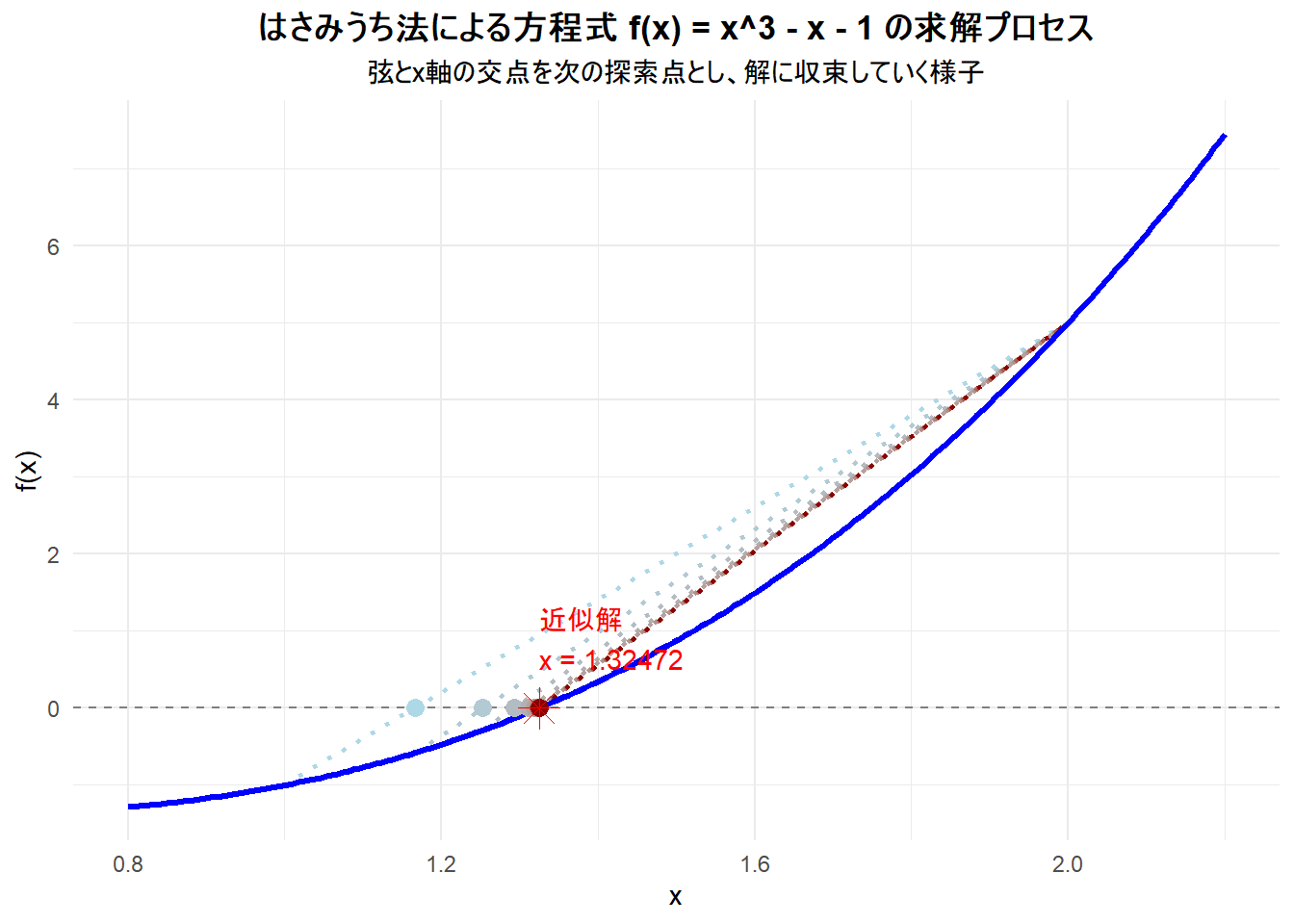
Figure 1 の読み方
- 青い曲線: 対象関数
f(x) = x^3 - x - 1のグラフです。 - 灰色の破線:
y=0のライン(x軸)です。 - 点線の弦: 各反復ステップで、区間の両端
(a, f(a))と(b, f(b))を結んだ直線です。色が水色から赤色になるにつれて、反復が進んでいることを示します。 - x軸上の色のついた点: 上記の弦がx軸と交わる点、すなわち次の近似解
cを示しています。 - 赤い星印: 最終的に得られた近似解です。
Figure 1 を見ると、どのステップでも弦の右端の点(x=2)が固定されたまま、左端の点だけが徐々に解に近づいている様子がよくわかります。
以上です。