Rで ハレー法 を試みます。
本ポストはこちらの続きです。

Rでニュートン法
Rで ニュートン法 を試みます。本ポストはこちらの続きです。1. ニュートン法とはニュートン法(またはニュートン・ラフソン法)は、方程式 f(x) = 0 の解を求めるための反復法です。これまでの手法が関数の値 f(x) のみに着目していた...
1. ハレー法とは
ハレー法(Halley’s Method)は、ニュートン法と同じくf(x)=0の解を求める反復法ですが、関数の1階導関数 f'(x) に加えて、2階導関数 f''(x) まで利用する点が特徴です。
基本的なアイデア:接線から接曲線へ
- ニュートン法: 点
(x_n, f(x_n))における、接線(1次近似)を利用しました。 - ハレー法: 点
(x_n, f(x_n))における、接する双曲線(2次近似の一種)を利用して次の点を予測します。
関数 f(x) をテイラー展開すると、
f(x) ≈ f(x_n) + f'(x_n)(x - x_n) + (f''(x_n)/2)(x - x_n)²
ニュートン法はこの式の2次の項を無視しましたが、ハレー法はこの2次の項まで考慮に入れます。ただし、この2次方程式をそのまま解くのではなく、変形によって反復計算式を導出します。
その結果として得られるハレー法の反復計算式は、以下のようになります。
x_{n+1} = x_n - (2 * f(x_n) * f'(x_n)) / (2 * (f'(x_n))² - f(x_n) * f''(x_n))
この式は一見複雑ですが、ニュートン法の反復式に補正項が加わった形と見ることができます。
x_{n+1} = x_n - f(x_n) / f'(x_n) * [ 補正項 ]
この補正項が、2階導関数 f''(x) の情報を使って、より速い収束の役割を果たしています。
特徴
- 長所:
- 3次収束: 収束が速く、3次収束として知られています。これは、1回の反復で解の正しい桁数がほぼ3倍になることを意味します。誤差が
10^{-2}なら次は10^{-6}、その次は10^{-18}と、ニュートン法を超える速度で収束します。
- 3次収束: 収束が速く、3次収束として知られています。これは、1回の反復で解の正しい桁数がほぼ3倍になることを意味します。誤差が
- 短所:
- 2階導関数が必要:
f''(x)まで計算し、プログラムに組み込む必要があります。これはニュートン法よりもさらにハードルが高く、実用上の大きな制約となります。 - 計算コスト: 1回の反復計算で評価する関数の数が増えるため、計算コストが高くなります。
- ニュートン法と同様の弱点: 初期値への依存性や、
f'(x)≈0での不安定さといった弱点はニュートン法と同様に持っています。
- 2階導関数が必要:
2. R言語によるシミュレーションコードと実行結果
それでは、f(x) = x³ - x - 1 = 0 をハレー法で解きます。 この場合、1階導関数は f'(x) = 3x² - 1、2階導関数は f''(x) = 6x となります。
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
# -----------------------------------------------------------------
# 1. 関数、1階導関数、2階導関数を定義
# -----------------------------------------------------------------
# f(x) = x^3 - x - 1
f <- function(x) {
return(x^3 - x - 1)
}
# f'(x) = 3x^2 - 1
f_prime <- function(x) {
return(3 * x^2 - 1)
}
# f''(x) = 6x
f_double_prime <- function(x) {
return(6 * x)
}
# -----------------------------------------------------------------
# 2. ハレー法のシミュレーションを行う関数を定義
# -----------------------------------------------------------------
halley_simulation <- function(func, func_prime, func_double_prime, x0, tol = 1e-15, max_iter = 10) {
cat("--- ハレー法シミュレーション開始 ---\n\n")
cat(sprintf("対象関数: x^3 - x - 1\n"))
cat(sprintf("初期値: x0 = %.1f\n", x0))
cat(sprintf("許容誤差: %e\n\n", tol))
x <- x0
history <- data.frame(
iter = integer(),
x = double(),
fx = double(),
x_new = double(),
fx_new = double()
)
for (i in 1:max_iter) {
fx <- func(x)
f_prime_x <- func_prime(x)
f_double_prime_x <- func_double_prime(x)
# 分母がゼロに近い場合は停止
denominator <- 2 * f_prime_x^2 - fx * f_double_prime_x
if (abs(denominator) < 1e-12) {
cat("計算式の分母がゼロに近いため、計算を停止します。\n")
break
}
# ハレー法の反復式
x_new <- x - (2 * fx * f_prime_x) / denominator
fx_new <- func(x_new)
cat(sprintf("【反復 %d回目】\n", i))
cat(sprintf(" 現在の点 x = %.15f\n", x))
cat(sprintf(" 次の近似解 x_new = %.15f\n", x_new))
cat(sprintf(" その関数値 f(x_new) = %.2e\n", fx_new))
history <- rbind(history, data.frame(
iter = i, x = x, fx = fx,
x_new = x_new, fx_new = fx_new
))
# 収束判定
if (abs(x_new - x) < tol) {
cat("\n--- 収束しました ---\n\n")
x <- x_new
break
}
x <- x_new
}
if (i == max_iter) {
cat("\n--- 最大反復回数に達しました ---\n")
}
cat(sprintf("最終的な解の近似値 = %.15f\n", x))
return(history)
}
# -----------------------------------------------------------------
# 3. シミュレーションの実行
# -----------------------------------------------------------------
sim_history_halley <- halley_simulation(f, f_prime, f_double_prime, x0 = 2.0)
# -----------------------------------------------------------------
# 4. ggplot2による結果の可視化 (2つのグラフを生成)
# -----------------------------------------------------------------
# --- グラフ1: 収束プロット ---
final_solution_value <- tail(sim_history_halley, 1)$x_new
halley_process_plot <- ggplot(sim_history_halley, aes(x = iter, y = x_new)) +
geom_hline(yintercept = final_solution_value, linetype = "dashed", color = "red", linewidth = 1) +
geom_text(aes(x = 0.5, y = final_solution_value, label = sprintf("真の解\n(約 %.6f)", final_solution_value)),
color = "red", hjust = 0, vjust = -0.2
) +
geom_line(color = "gray50", linewidth = 1) +
geom_point(color = "darkgreen", size = 5, stroke = 1.5) +
labs(
title = "ハレー法の収束プロセス",
x = "反復回数 (iter)",
y = "近似解 (x_new) の値"
) +
scale_x_continuous(breaks = 1:nrow(sim_history_halley)) +
theme_minimal(base_family = "sans")
# --- グラフ2: 求解プロセスの可視化 ---
curve_data <- data.frame(x = seq(1.2, 2.1, length.out = 200)) %>%
mutate(y = f(x))
final_solution_point <- tail(sim_history_halley, 1)
visualization_plot <- ggplot() +
geom_hline(yintercept = 0, linetype = "dashed", color = "gray50") +
geom_line(data = curve_data, aes(x = x, y = y), color = "blue", linewidth = 1.2) +
# 各ステップの(x, f(x))から(x_new, 0)への移動を表現
geom_segment(
data = sim_history_halley,
aes(x = x, y = fx, xend = x_new, yend = 0, color = iter),
arrow = arrow(length = unit(0.2, "cm")), # 矢印で表現
linewidth = 1
) +
geom_point(data = sim_history_halley, aes(x = x, y = fx, color = iter), size = 4) +
geom_point(aes(x = final_solution_point$x_new, y = 0), size = 5, shape = 8, color = "red") +
geom_text(
aes(
x = final_solution_point$x_new, y = 0.5,
label = sprintf("近似解\nx = %.5f", final_solution_point$x_new)
),
color = "red", hjust = 0, vjust = 0
) +
scale_color_gradient(low = "lightgreen", high = "darkgreen") +
labs(
title = "ハレー法による求解プロセス",
x = "x", y = "f(x)"
) +
theme_minimal(base_family = "sans") +
theme(legend.position = "none")
# 2つのプロットを表示
print(halley_process_plot)
print(visualization_plot)--- ハレー法シミュレーション開始 ---
対象関数: x^3 - x - 1
初期値: x0 = 2.0
許容誤差: 1.000000e-15
【反復 1回目】
現在の点 x = 2.000000000000000
次の近似解 x_new = 1.395604395604396
その関数値 f(x_new) = 3.23e-01
【反復 2回目】
現在の点 x = 1.395604395604396
次の近似解 x_new = 1.324917597860574
その関数値 f(x_new) = 8.52e-04
【反復 3回目】
現在の点 x = 1.324917597860574
次の近似解 x_new = 1.324717957249788
その関数値 f(x_new) = 2.15e-11
【反復 4回目】
現在の点 x = 1.324717957249788
次の近似解 x_new = 1.324717957244746
その関数値 f(x_new) = 2.22e-16
【反復 5回目】
現在の点 x = 1.324717957244746
次の近似解 x_new = 1.324717957244746
その関数値 f(x_new) = 2.22e-16
--- 収束しました ---
最終的な解の近似値 = 1.324717957244746注目点: ニュートン法では7回の反復で収束しましたが、ハレー法では 5回の反復で、許容誤差
1e-15(倍精度浮動小数点数の限界に近い)をクリアしました。
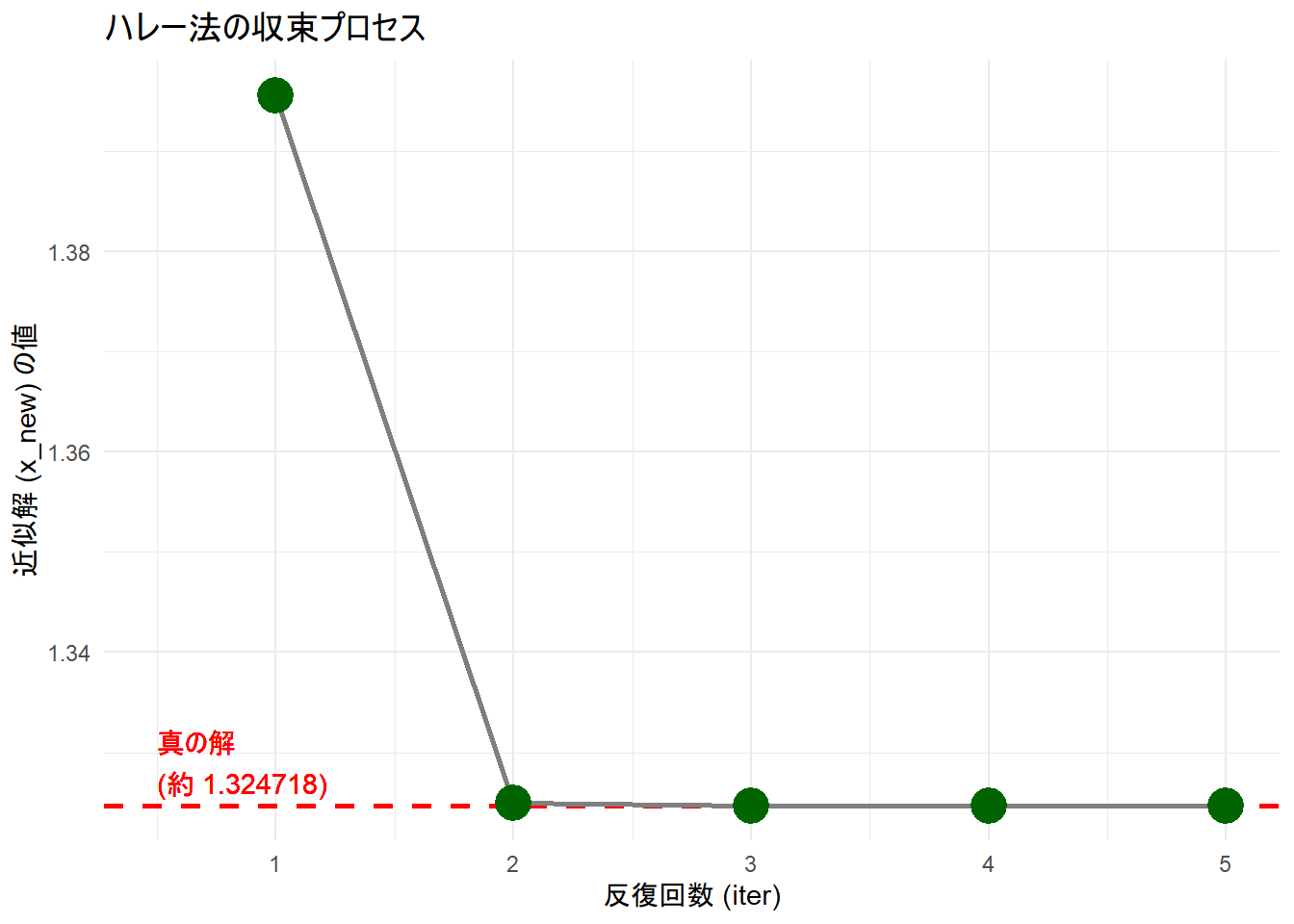
Figure 1 の読み方
- 横軸: 反復回数、縦軸: 近似解の値。
- 赤い破線: 真の解。
- 緑の点と灰色の線: 近似解の推移。4ステップで真の解に「張り付いて」しまう、その収束の速さが視覚的にわかります。
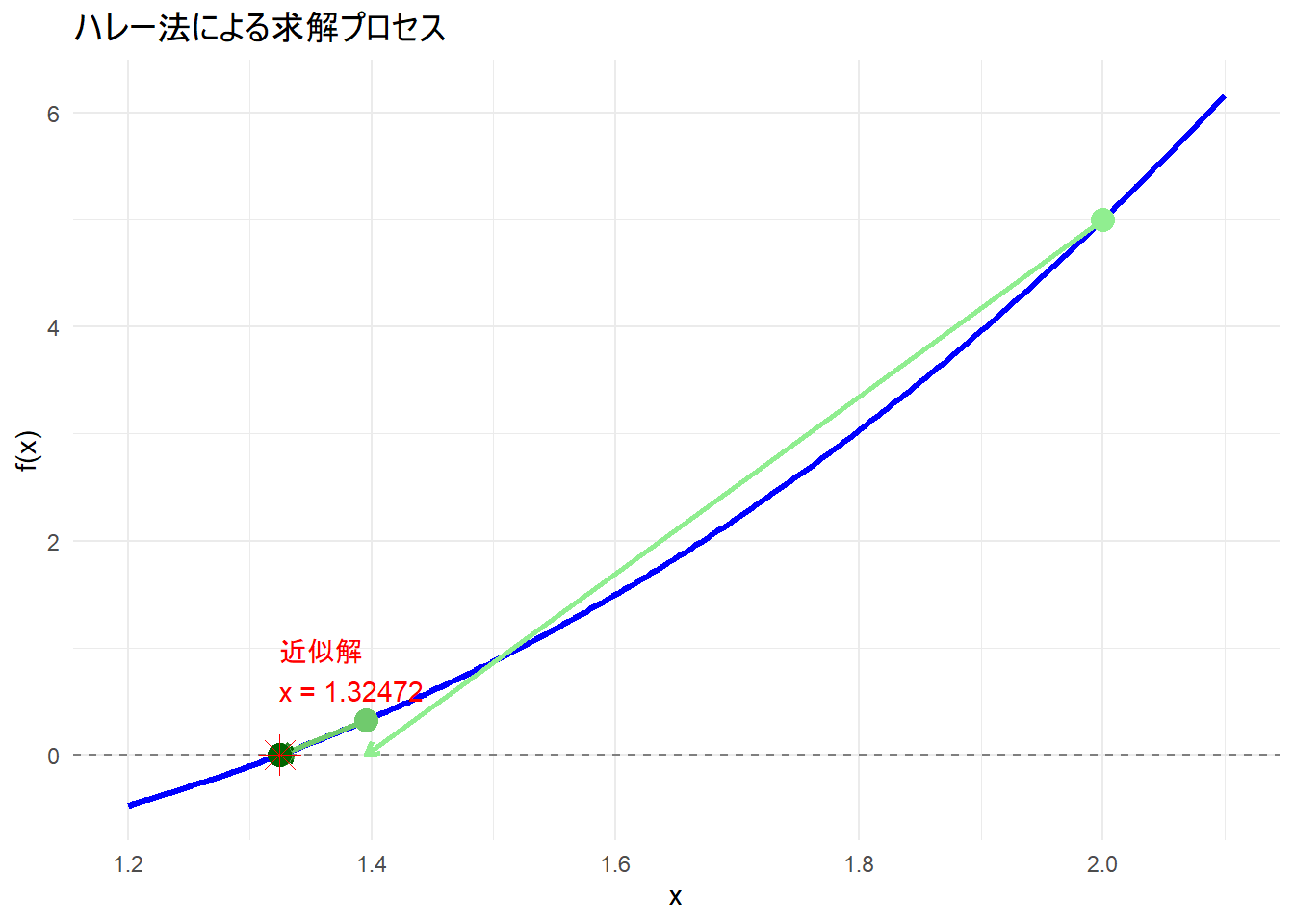
Figure 2 の読み方
- 青い曲線:
f(x)のグラフ。 - 色のついた矢印: 各ステップでの近似解の移動を示します。
x_nから、より精密に予測されたx_{n+1}へと、大きなジャンプで解に近づいている様子がわかります。 - 2回目の反復(中間色の矢印)が終わった時点で、すでに出発点が解のすぐ近くまで来ていることが確認できます。
以上です。