Rで微分方程式:1階常微分方程式

1.1 1階常微分方程式とは？

一言でいうと、「ある量の変化の速さ（変化率）が、その時々のある量や時間によって決まる」という関係を記述した方程式です。

数式では、求めたい関数を y(t)（時間 t の関数 y）、その変化率を dy/dt と書きます。1階常微分方程式は、これらを含む以下のような形で表現されます。

dy/dt = f(t, y)

• t: 時間などの独立変数
• y(t): 求めたい未知の関数（例：人口、温度、位置など）
• dy/dt: y の t に対する変化率（導関数）
• f(t, y): 変化率が t と y によってどのように決まるかを表す関数

1.2 具体例：ロジスティック方程式

現実世界の現象をモデル化する際によく使われる「ロジスティック方程式」を例に見てみましょう。これは、生物の個体数など、上限のある成長を表すモデルです。

dP/dt = r * P * (1 - P/K)

• P(t): 時刻 t における個体数
• dP/dt: 個体数の増加速度
• r: 内的自然増加率（個体数が少ないときの増加率）
• K: 環境収容力（その環境が支えられる個体数の上限）

この式が意味することは以下の通りです。

• 個体数 P が 0 に近いとき、(1 - P/K) はほぼ 1 になり、dP/dt ≈ rP となります。これは「増加速度は個体数に比例する」という指数関数的な成長を示します。
• 個体数 P が環境収容力 K に近づくと、(1 - P/K) は 0 に近づき、増加速度 dP/dt も 0 に近づきます。つまり、成長が頭打ちになります。
• もし P が K を超えると (1 - P/K) は負になり、dP/dt も負になるため、個体数は減少して K に近づきます。

1.3 初期値問題と数値解法

この方程式を解く（積分する）と、P(t) の具体的な形がわかりますが、そのためには「いつ、個体数が何匹だったか」という情報、つまり初期値（例：t=0 のとき P(0) = 10）が必要です。

微分方程式と初期値のセットを「初期値問題」と呼びます。

しかし、多くの常微分方程式は、手計算で厳密な解（解析解）を求めるのが困難、あるいは不可能です。そこで、コンピュータを使って近似的な解を計算する「数値解法」が強力なツールとなります。

最も単純な数値解法はオイラー法です。これは、微小な時間 Δt だけ未来の状態を、現在の変化率を使って予測する方法です。

P(t + Δt) ≈ P(t) + (dP/dt) * Δt

この計算を短い時間間隔で繰り返し行うことで、P(t) の時間変化の様子（シミュレーション結果）を得ることができます。

1.4 常微分方程式の階数

微分方程式の「階数（かいすう）」は、その方程式に含まれる導関数の最大の階数によって決まります。

今回のロジスティック方程式を再確認してみましょう。

dP/dt = r * P * (1 - P/K)

この方程式に含まれる導関数は dP/dt のみです。これは P を t で1回微分したものです（1階の導関数）。

方程式の中に2階以上の導関数（例：d²P/dt²）は含まれていません。したがって、この方程式は1階の常微分方程式に分類されます。

簡単に言えば、「求めたい関数の変化率（速度）そのものを記述する式」が1階常微分方程式です。

1.5 2階常微分方程式との比較

理解を深めるために、物理学でよく登場する2階常微分方程式の例を見てみましょう。ばねの振動（単振動）を記述する運動方程式が代表的です。

m * (d²x/dt²) = -k * x

• x(t): 時刻 t における、つり合いの位置からの変位（位置）
• d²x/dt²: 変位 x の時間に対する2階導関数（加速度）
• m: おもりの質量
• k: ばね定数

この方程式には、2階の導関数 d²x/dt² が含まれています。これがこの方程式の中で最も階数の高い導関数なので、これは2階の常微分方程式です。

物理的な意味合いは以下のようになります。

• 1階 (ロジスティック方程式): 個体数の「増加速度」が、現在の個体数によって決まる。
• 2階 (ばねの振動): おもりの「加速度」が、現在の位置によって決まる。（ニュートンの運動法則 F=ma の形）

2.1 準備：必要なパッケージの読み込み

まず、シミュレーションと可視化に必要なパッケージを読み込みます。

# パッケージの読み込み
library(deSolve)
library(ggplot2)
library(dplyr)

2.2 シミュレーションの実行 (deSolve パッケージ)

# ロジスティック方程式を定義する関数
# t: 時間, y: 状態変数（ここでは個体数P）, params: パラメータ（rとK）
logistic_model <- function(t, y, params) {
  # 状態変数をわかりやすい変数名に割り当てる
  P <- y[1]

  # パラメータをリストから取り出す
  r <- params$r
  K <- params$K

  # 微分方程式（dP/dt）を計算
  dP_dt <- r * P * (1 - P / K)

  # 結果をリストで返す
  return(list(dP_dt))
}

# パラメータをリストとして設定
# r: 内的自然増加率, K: 環境収容力
params <- list(r = 0.8, K = 1000)

# 初期値を名前付きベクトルで設定
# t=0 のときの個体数 P = 10
initial_y <- c(P = 10)

# 計算する時間点を設定 (0から20まで、0.1刻み)
times <- seq(from = 0, to = 20, by = 0.1)

# シミュレーションの条件をコンソールに表示
cat("--- シミュレーション条件 ---\n\n")
cat(sprintf("モデル: ロジスティック方程式\n"))
cat(sprintf("パラメータ: r = %.2f, K = %.0f\n", params$r, params$K))
cat(sprintf("初期個体数: P(0) = %.0f\n", initial_y["P"]))

--- シミュレーション条件 ---

モデル: ロジスティック方程式
パラメータ: r = 0.80, K = 1000
初期個体数: P(0) = 10

# deSolve::ode関数でシミュレーションを実行
# y: 初期値, times: 時間点, func: 微分方程式の関数, parms: パラメータ
output <- ode(y = initial_y, times = times, func = logistic_model, parms = params)

Step 4: 結果の可視化

ode 関数の出力をデータフレームに変換し、グラフを描画します。

# 結果をデータフレームに変換
output_df <- as.data.frame(output)

# ggplotで結果をプロット
p <- ggplot(output_df, aes(x = time, y = P)) +
  geom_line(color = "dodgerblue", linewidth = 1.2) + # 折れ線グラフ
  geom_hline(yintercept = params$K, linetype = "dashed", color = "red") + # 環境収容力Kの水平線
  annotate("text",
    x = max(times) * 0.8, y = params$K * 0.9,
    label = paste("環境収容力 (K =", params$K, ")"), color = "red"
  ) +
  labs(
    title = "ロジスティック方程式による個体数の時間変化",
    subtitle = "最初は指数関数的に増加し、やがて環境収容力に収束する",
    x = "時間 (t)",
    y = "個体数 (P)",
    caption = "deSolveパッケージによる数値シミュレーション結果"
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(size = 18, face = "bold"),
    plot.subtitle = element_text(size = 12),
    axis.title = element_text(size = 14)
  )

# グラフを表示
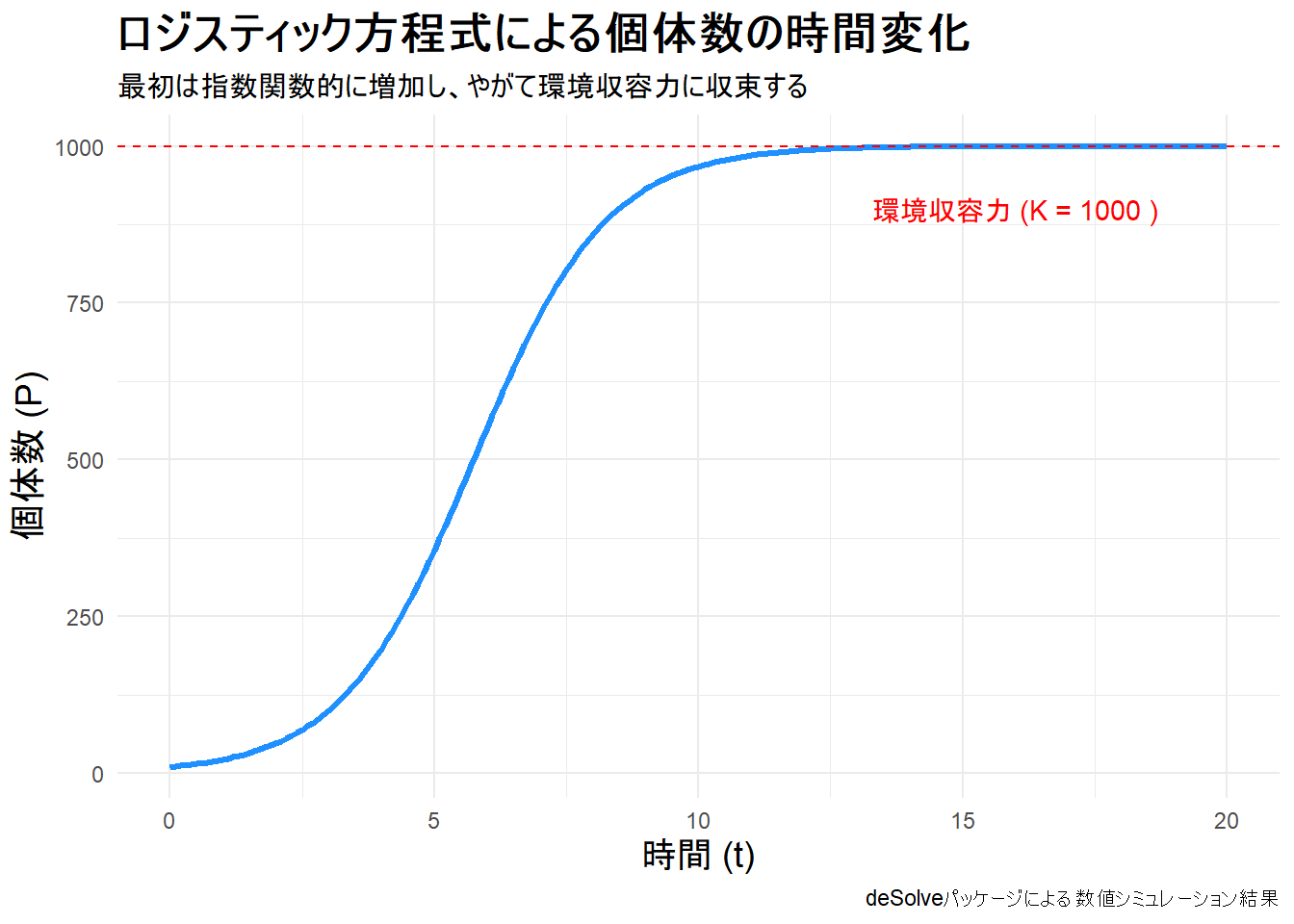
print(p)

Figure 1 から、ロジスティック方程式が示す以下の特徴を視覚的に理解できます。

• S字カーブ（シグモイド曲線）: 個体数は、最初はゆっくりと、次に急激に増加し、最終的には増加が緩やかになって環境収容力 K=1000 に収束していきます。
• 現実的な成長: 無限に増え続けるのではなく、環境の限界によって成長が頭打ちになる、より現実的な個体数の変動を表現しています。

以上です。