Rで微分方程式:2階常微分方程式

Rで 微分方程式:2階常微分方程式 を試みます。

本ポストはこちらの続きです。

Rで微分方程式:1階常微分方程式を試みます。1. 1階常微分方程式の概要1.1 1階常微分方程式とは？一言でいうと、「ある量の変化の速さ（変化率）が、その時々のある量や時間によって決まる」という関係を記述した方程式です。数式では、求めた...

1. 2階常微分方程式の概要

1.1 2階常微分方程式とは？

1階が「変化の速さ（速度）」を記述する方程式だったのに対し、2階は「変化の速さの変化の速さ（加速度）」を記述する方程式です。

数式では、求めたい関数を x(t)、その1階導関数（速度）を dx/dt、2階導関数（加速度）を d²x/dt² と書きます。2階常微分方程式は、これらを含む以下のような形で表現されます。

d²x/dt² = f(t, x, dx/dt)

これは、「加速度 d²x/dt² が、その時々の時間 t、位置 x、そして速度 dx/dt によって決まる」という関係を表しています。

1.2 具体例：減衰振動（ばねとおもりのモデル）

壁にばねで繋がれたおもりが、空気抵抗のような抵抗を受けながら振動する動きを考えてみましょう。これは典型的な2階常微分方程式でモデル化できます。

ニュートンの運動方程式 F = ma（力 = 質量 × 加速度）を元に式を立てます。おもりにかかる力は以下の2つです。

ばねの復元力: F_spring = -k * x （フックの法則。位置 x に比例し、常に中心に戻ろうとする力）
減衰力（抵抗力）: F_damping = -c * (dx/dt) （速度 dx/dt に比例し、常に動きを妨げる向きに働く力）

これらを運動方程式に代入すると、

m * (d²x/dt²) = -k * x - c * (dx/dt)

整理すると、以下の2階常微分方程式が得られます。

m * d²x/dt² + c * dx/dt + k * x = 0

x(t): 時刻 t における、つり合いの位置からの変位（位置）
dx/dt: 速度
d²x/dt²: 加速度
m: おもりの質量
c: 減衰係数（抵抗の強さ）
k: ばね定数（ばねの硬さ）

1.3 数値解法のための「連立1階化」

deSolve のような標準的なソルバーは、1階の（連立）微分方程式を解くように設計されています。そのため、この2階の方程式を解くには、2つの1階常微分方程式の組（連立方程式）に変換するというテクニックを使います。

新しい変数を導入する まず、速度 v という新しい変数を v(t) = dx/dt と定義します。これは1つ目の1階方程式になります。
- 式1: dx/dt = v
元の方程式を書き換える 次に、元の2階方程式を d²x/dt² について解きます。
d²x/dt² = (-k * x - c * (dx/dt)) / m
ここで d²x/dt² は速度 v の変化率 dv/dt であり、dx/dt は v なので、
- 式2: dv/dt = (-k * x - c * v) / m

これで、1つの2階常微分方程式を、位置 x と速度 v に関する2つの1階常微分方程式の組に変換できました。この形にすれば、ソルバーで解くことができます。

2. シミュレーションのためのRコード

それでは、Rで減衰振動のシミュレーションを行い、おもりの動きを可視化してみましょう。

2.1 準備（パッケージ読み込み）

前回と同様に、必要なパッケージを読み込みます。

library(deSolve)
library(ggplot2)
library(dplyr)

2.2 シミュレーションの実行

Step 1: 微分方程式の定義（連立1階化した形で）

連立化した2つの1階方程式をRの関数として定義します。状態変数 y は、y[1] を位置 x、y[2] を速度 v とします。

# 減衰振動モデルを定義する関数
# t: 時間, y: 状態変数ベクトル (y[1]=x, y[2]=v), params: パラメータ
damped_oscillation_model <- function(t, y, params) {
  # 状態変数をわかりやすい変数名に割り当てる
  x <- y[1] # 位置
  v <- y[2] # 速度

  # パラメータをリストから取り出す
  m <- params$m # 質量
  k <- params$k # ばね定数
  c <- params$c # 減衰係数

  # 2つの1階微分方程式を計算
  # dx/dt = v
  dx_dt <- v

  # dv/dt = (-k*x - c*v) / m
  dv_dt <- (-k * x - c * v) / m

  # 結果（2つの微分値）をリストで返す
  return(list(c(dx_dt, dv_dt)))
}

Step 2: パラメータと初期条件の設定

今回は「位置」と「速度」の2つの初期値が必要です。ここでは、「ばねを x=1 の位置まで引っ張って、静かに（v=0）手を離す」状況を想定します。

# パラメータをリストとして設定
# m: 質量, k: ばね定数, c: 減衰係数
params <- list(m = 1.0, k = 5.0, c = 0.5)

# 初期値をベクトルで設定
# x(0) = 1 (位置), v(0) = 0 (速度)
initial_y <- c(x = 1.0, v = 0.0)

# 計算する時間点を設定 (0から20まで)
times <- seq(from = 0, to = 20, by = 0.05)

# シミュレーションの条件をコンソールに表示
cat("--- シミュレーション条件 ---\n\n")
cat("モデル: 減衰振動（2階常微分方程式）\n")
cat(sprintf("パラメータ: m=%.1f, k=%.1f, c=%.1f\n", params$m, params$k, params$c))
cat(sprintf("初期条件: 位置 x(0)=%.1f, 速度 v(0)=%.1f\n", initial_y["x"], initial_y["v"]))

--- シミュレーション条件 ---

モデル: 減衰振動（2階常微分方程式）
パラメータ: m=1.0, k=5.0, c=0.5
初期条件: 位置 x(0)=1.0, 速度 v(0)=0.0

Step 3: ソルバーの実行

ode 関数に、連立方程式のモデルと2つの初期値を渡して実行します。

# deSolve::ode関数でシミュレーションを実行
output <- ode(y = initial_y, times = times, func = damped_oscillation_model, parms = params)

Step 4: 結果の可視化 (`ggplot2`)

結果のデータフレームには time, x, v の3列が含まれます。ここではおもりの位置 x の時間変化をプロットします。

# 結果をデータフレームに変換
output_df <- as.data.frame(output)

# ggplotで結果をプロット
p <- ggplot(output_df, aes(x = time, y = x)) +
  geom_line(color = "darkcyan", linewidth = 1.2) + # 折れ線グラフ
  geom_hline(yintercept = 0, linetype = "dashed", color = "gray50") + # つり合いの位置(x=0)の線
  labs(
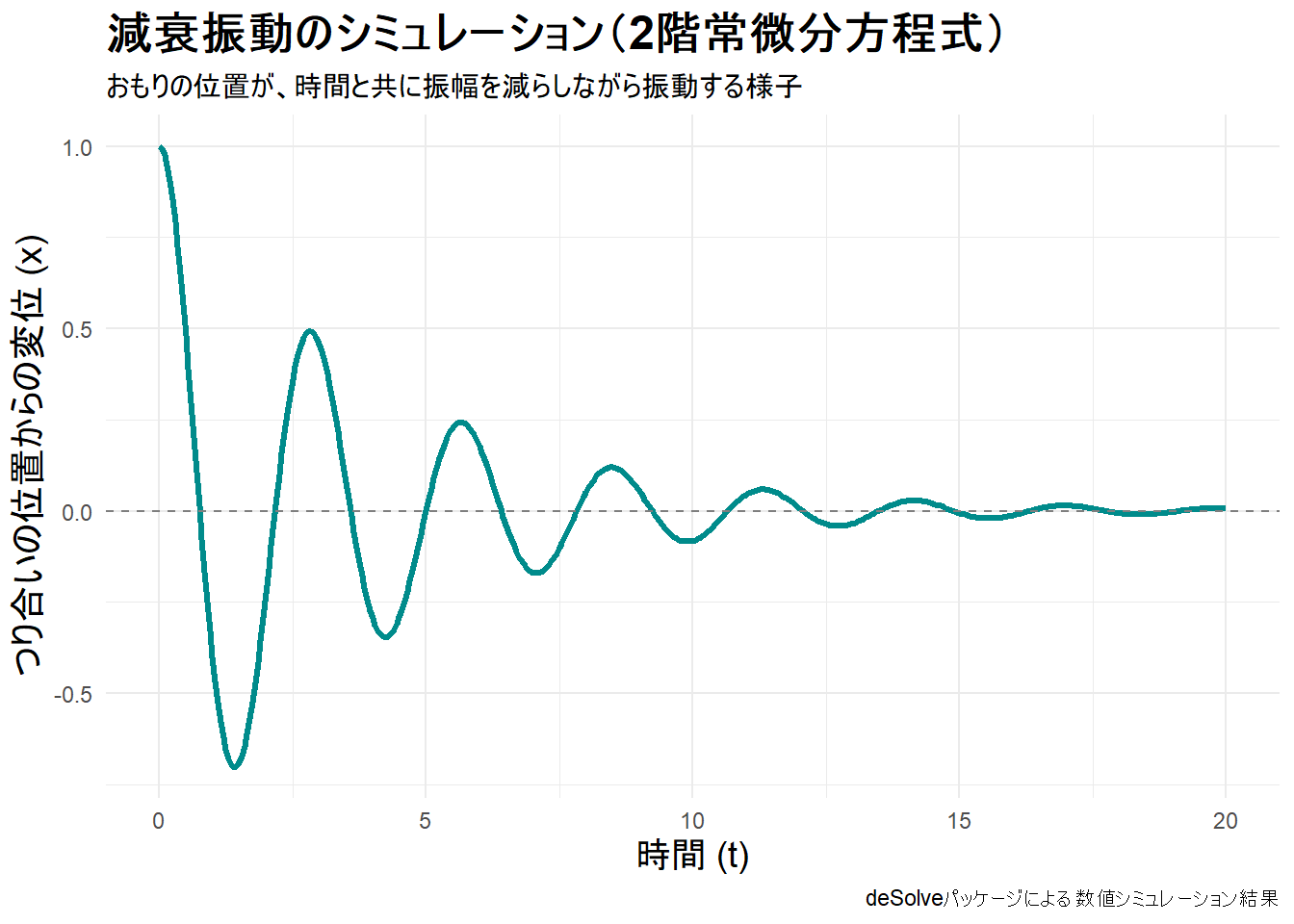
    title = "減衰振動のシミュレーション（2階常微分方程式）",
    subtitle = "おもりの位置が、時間と共に振幅を減らしながら振動する様子",
    x = "時間 (t)",
    y = "つり合いの位置からの変位 (x)",
    caption = "deSolveパッケージによる数値シミュレーション結果"
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(size = 18, face = "bold"),
    plot.subtitle = element_text(size = 12),
    axis.title = element_text(size = 14)
  )

# グラフを表示
print(p)