Rで微分方程式:2階偏微分方程式

1.1 2階偏微分方程式とは？

1階偏微分方程式が「時間変化率と空間勾配」の関係を記述したのに対し、2階偏微分方程式は、時間や空間に関する2階の偏導関数を含みます。これにより、より複雑で動的な現象をモデル化できます。

代表的な例が、加速度（時間の2階微分）と空間的な曲がり具合（空間の2階微分）の関係を記述する方程式です。

1.2 具体例：1次元波動方程式

ギターの弦や太鼓の膜の振動は、「波動方程式」と呼ばれる2階偏微分方程式で記述されます。

∂²u/∂t² = c² * ∂²u/∂x²

• u(t, x): 時刻 t、位置 x における弦の変位（上下方向のズレ）
• c: 波が伝わる速さ（弦の材質や張力で決まる）
• ∂²u/∂t²: ある点 x に固定したときの、変位 u の加速度。
• ∂²u/∂x²: ある時刻 t に固定したときの、弦の形の「曲がり具合（曲率）」を表す。

この式の物理的な意味は、「弦のある点の加速度は、その点の曲がり具合に比例する」ということです。

• 弦が大きく下に凸に曲がっている点（∂²u/∂x² > 0）では、上向きの加速度が生じ、中心に戻ろうとします。
• 弦が大きく上に凸に曲がっている点（∂²u/∂x² < 0）では、下向きの加速度が生じます。
• 弦がまっすぐな点（∂²u/∂x² = 0）では、加速度は0です。

この単純なルールが、波の伝播、反射、干渉といった複雑な振る舞いを生み出します。

1.3 数値解法（中心差分法）

この方程式を数値的に解くために、時間と空間の両方を微小なステップ Δt, Δx で区切ります。ここでは、2階の偏導関数を「中心差分」で近似します。

∂²u/∂t² ≈ (u(t+Δt, x) - 2u(t, x) + u(t-Δt, x)) / (Δt)²

∂²u/∂x² ≈ (u(t, x+Δx) - 2u(t, x) + u(t, x-Δx)) / (Δx)²

これらを波動方程式に代入し、未来の状態 u(t+Δt, x) について整理すると、次の時間ステップの変位を計算する更新式が得られます。

この更新式の特徴は、未来の状態を計算するために、現在と過去の2つの時刻の情報が必要になる点です。これは、方程式が時間の2階微分を含んでいることに対応しています。

2.1 準備：必要なパッケージの読み込み

# パッケージの読み込み
library(ggplot2)
library(dplyr)
library(gganimate)

2.2 シミュレーションの実行

# --- シミュレーションパラメータ ---
L <- 10.0 # 弦の長さ (0 <= x <= L)
Nx <- 100 # 空間の分割数
dx <- L / Nx # 空間ステップ幅
c_wave <- 1.0 # 波の伝播速度
T_end <- 20.0 # シミュレーション終了時間
# 安定性条件 (クーラン条件) を満たすように時間ステップを設定
CFL <- 0.5
dt <- CFL * dx / c_wave

# --- 初期条件とグリッドの設定 ---
# 空間グリッド (x座標)
x <- seq(0, L, by = dx)

# 初期形状 u(t=0, x) を三角形で作成
# 弦の中央(L/2)で高さ1になるように持ち上げる
u_initial <- pmin(2 * x / L, 2 * (L - x) / L)
# 振動の振幅が大きすぎるので調整
u_initial <- u_initial * 0.5

# 変位を格納するベクトルを3つの時刻分用意
u <- u_initial # 現在 (t) の変位
u_old <- u_initial # 過去 (t-Δt) の変位 (静かに手を離すので初期速度0を意味する)
u_new <- numeric(Nx + 1) # 未来 (t+Δt) の変位を計算するため

# 時間ステップの数
nsteps <- round(T_end / dt)

# 結果を保存するためのデータフレームを準備
results_df <- data.frame()

# シミュレーションの条件を表示
cat("--- シミュレーション条件 ---\n\n")
cat("モデル: 1次元波動方程式（2階偏微分方程式）\n")
cat(sprintf("波の速度: c = %.2f\n", c_wave))
cat(sprintf("空間: 0~%.1f, 時間: 0~%.1f\n", L, T_end))
cat("境界条件: 両端固定\n")
cat("--------------------------\n")

--- シミュレーション条件 ---

モデル: 1次元波動方程式（2階偏微分方程式）
波の速度: c = 1.00
空間: 0~10.0, 時間: 0~20.0
境界条件: 両端固定
--------------------------

# 時間発展の計算ループ
for (n in 0:nsteps) {
  # 現在のステップの結果をデータフレームに追加
  current_step_df <- data.frame(time = n * dt, x = x, u = u)
  results_df <- rbind(results_df, current_step_df)

  # 空間方向のループ（内側の点のみ計算）
  for (i in 2:Nx) {
    # 中心差分法による更新式
    term_t <- 2 * u[i] - u_old[i]
    term_x <- (c_wave * dt / dx)^2 * (u[i + 1] - 2 * u[i] + u[i - 1])
    u_new[i] <- term_t + term_x
  }

  # 境界条件: 両端固定 (常に変位0)
  u_new[1] <- 0
  u_new[Nx + 1] <- 0

  # 時刻を1ステップ進める
  u_old <- u
  u <- u_new
}

Step 3: 結果の可視化

# ggplotでアニメーションを作成
p_anim <- ggplot(results_df, aes(x = x, y = u, group = 1)) +
  geom_line(color = "mediumpurple", linewidth = 1.2) +
  geom_hline(yintercept = 0, color = "gray50") +
  scale_x_continuous(breaks = seq(0, L, by = 2)) +
  ylim(-0.6, 0.6) + # y軸の範囲を固定
  labs(
    title = "波動方程式のシミュレーション（弦の振動）",
    subtitle = "時刻: {round(frame_time, 2)}",
    x = "弦の位置 (x)",
    y = "変位 (u)",
    caption = "中心差分法による数値シミュレーション結果"
  ) +
  theme_minimal() +
  theme(
    plot.title = element_text(face = "bold", size = 28),
    plot.subtitle = element_text(size = 26),
    axis.title = element_text(size = 26),
    plot.caption = element_text(size = 26),
    axis.text.x = element_text(size = 26, color = "black"),
    axis.text.y = element_text(size = 26, color = "black")
  ) +
  # gganimateの設定
  transition_time(time) +
  ease_aes("linear")

# アニメーションをレンダリングして表示・保存
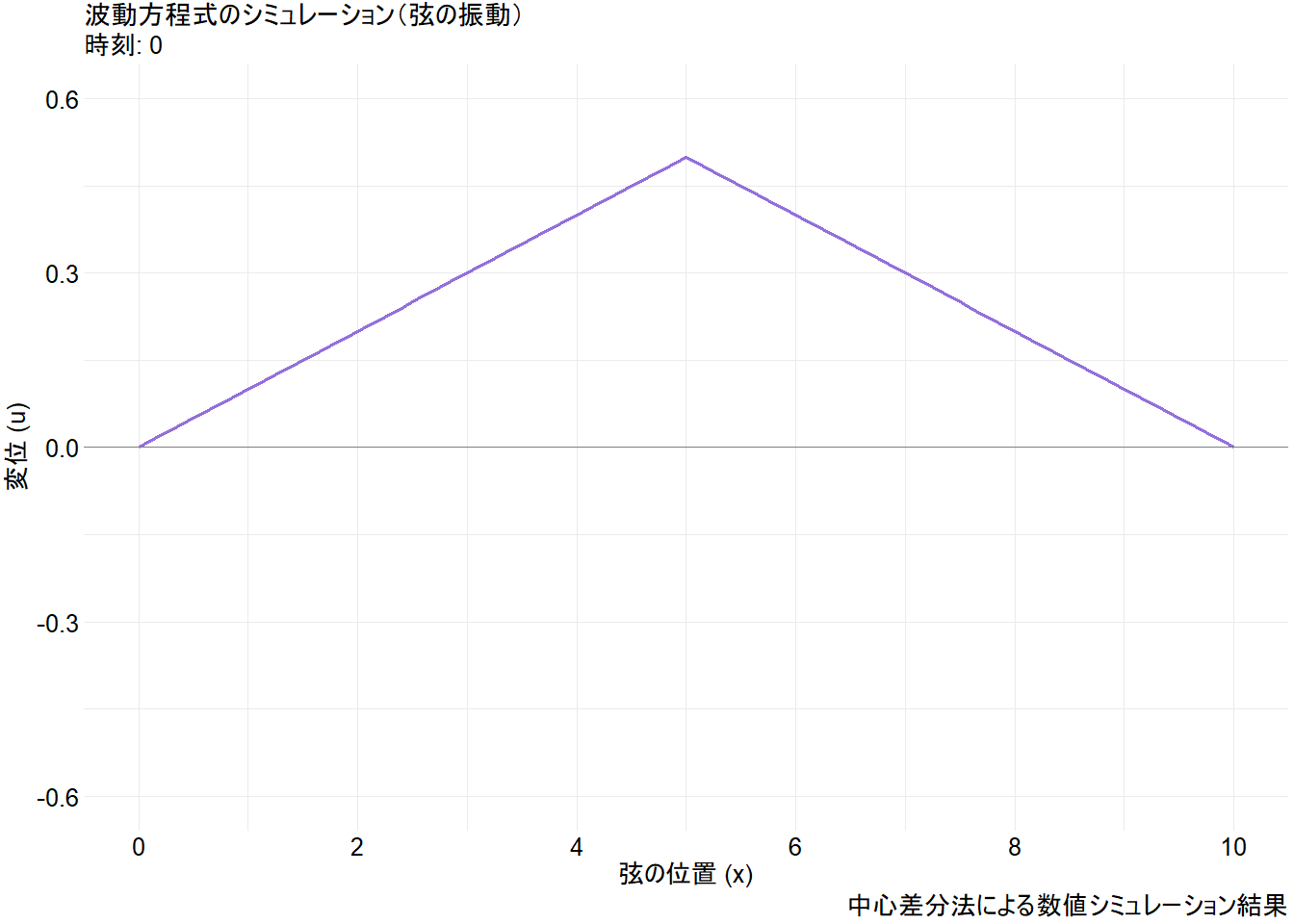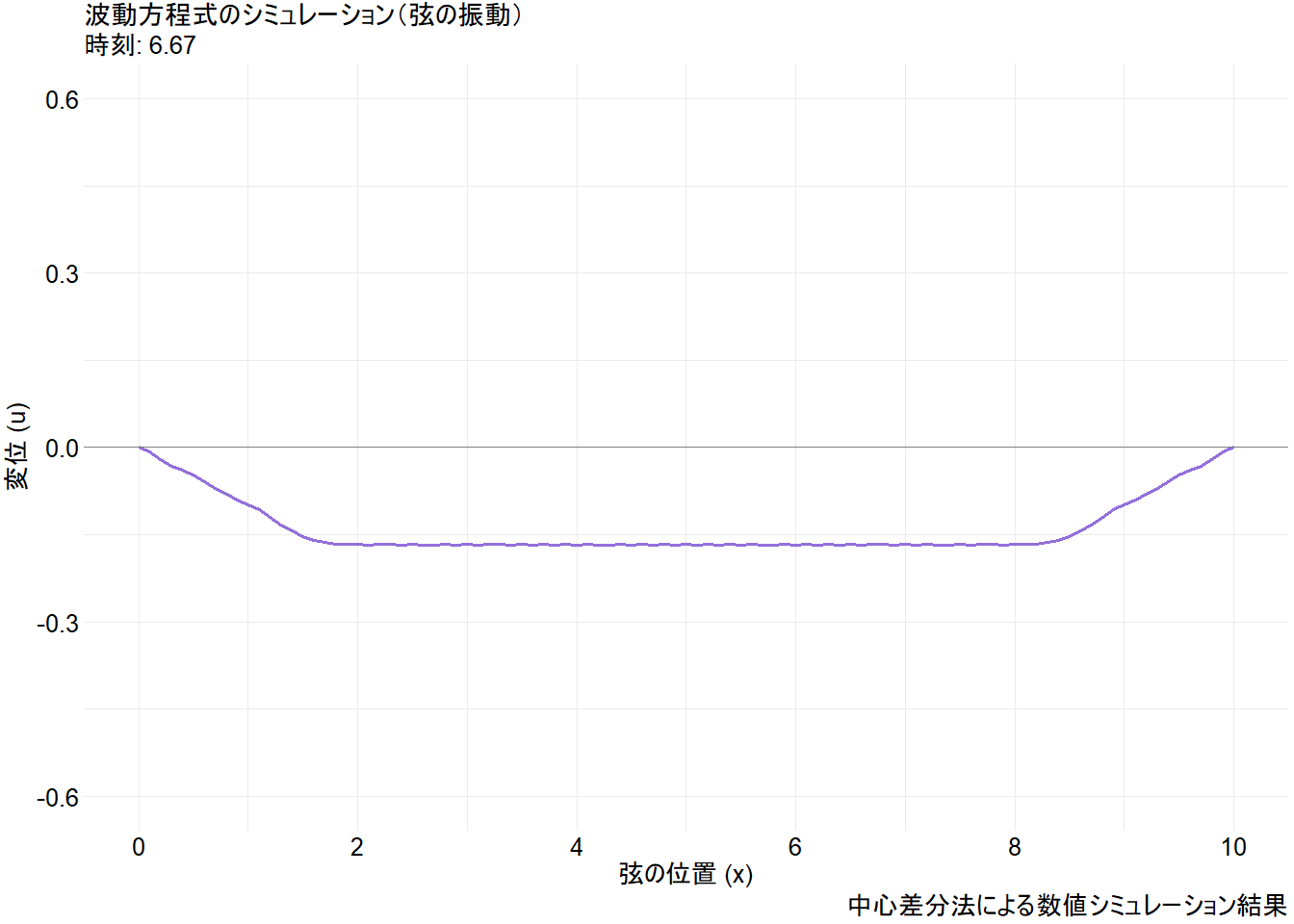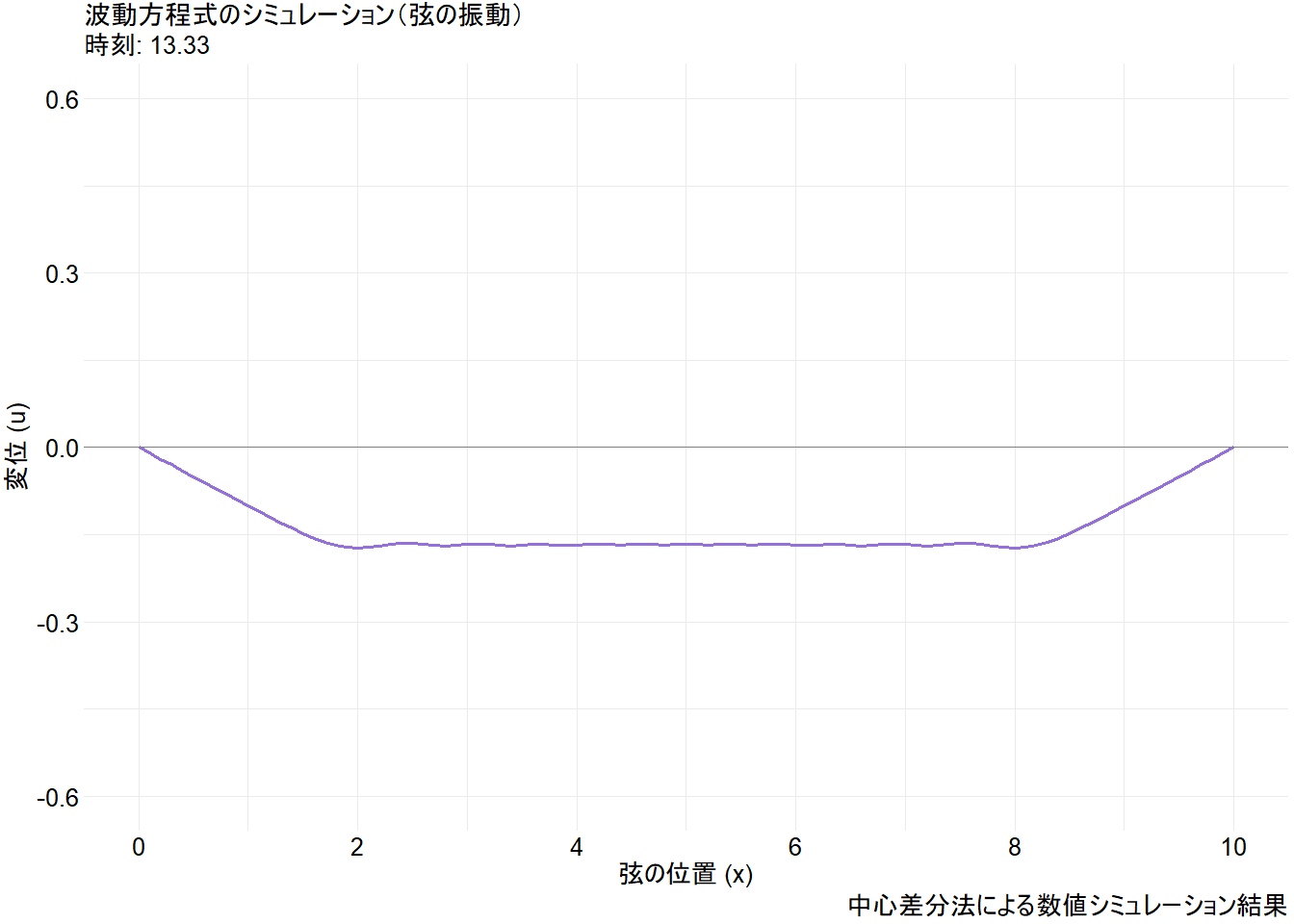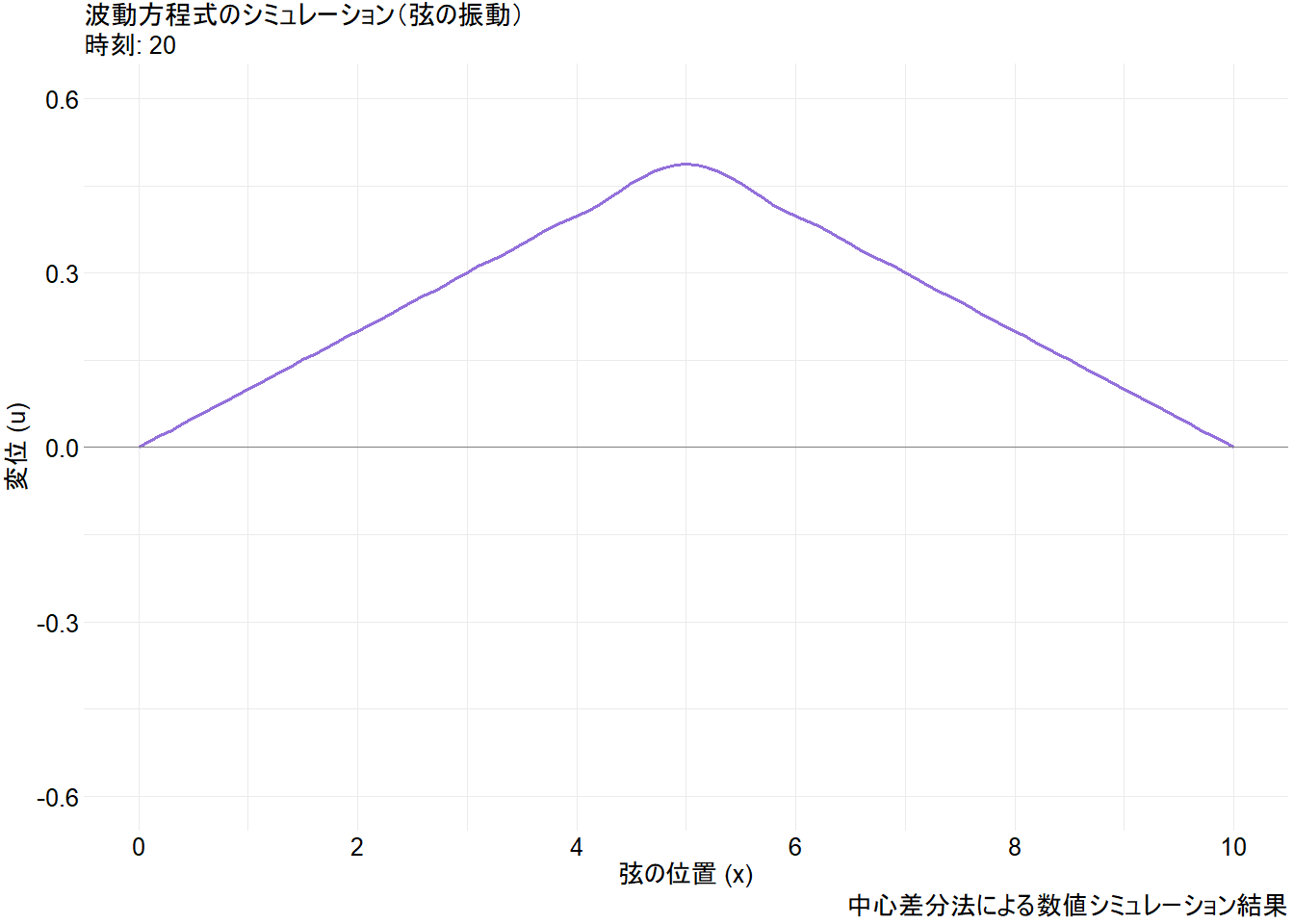
animate(p_anim, nframes = 250, fps = 25, width = 1344, height = 960, , renderer = gifski_renderer("wave_equation_simulation.gif"))

Figure 1 から、以下の点が視覚的に理解できます。

• 波の分裂と伝播: 初期の三角形の山は、右向きと左向きの2つの波に分裂して、それぞれ両端に向かって進んでいきます。
• 固定端反射: 波が両端（固定されている点）に到達すると、上下を反転（逆相に）して反射します。
• 干渉: 反射した2つの波は中央に向かって進み、互いにすれ違う際に足し合わされます（干渉）。
• 再現: t=L/c（このシミュレーションでは t=10）の時点で、2つの波は干渉し、元の三角形が上下反転した形で再現されます。その後、再び両端で反射し、t=2L/c（t=20）で最初の状態に戻ります。

1. 一言でいうと（直感的なアナロジー）

クーラン条件は、陽解法（未来の値を過去と現在の値だけから直接計算する方法）を用いる場合に、計算が破綻しないために、「シミュレーション内の波が、1時間ステップ（Δt）の間に、1空間ステップ（Δx）以上進んではいけない」というルールです。

電車と駅で例えてみましょう。

• 波: あなたが追いかけている電車
• 空間グリッド (x): 線路上の駅
• 時間ステップ (Δt): あなたが次の駅まで移動するのにかかる時間

もし、あなたが次の駅に着く前に、電車がその駅を通り過ぎてさらに先の駅まで行ってしまったら、あなたは電車の正確な位置を見失ってしまいます。シミュレーションでも同じことが起こります。

つまり、ある点 x の未来の値を、隣の点 x-Δx や x+Δx の現在の情報を使って計算する際、もし物理的な波が1ステップの時間で Δx より遠くまで伝わってしまうと、計算に必要な情報が届く前に波が通り過ぎてしまい、計算が物理的に無意味な、間違った結果を生み出してしまいます。

2. 数値計算における意味と数式

この条件は、ドイツの数学者リヒャルト・クーラン、クルト・フリードリヒス、ハンス・レヴィによって提唱されたため、クーラン・フリードリヒス・レヴィ条件（CFL条件）とも呼ばれます。

この条件は、「クーラン数（CFL数）」と呼ばれる無次元数 μ（ミュー）を使って表現されます。

μ = c * Δt / Δx

• c: 波の物理的な伝播速度
• Δt: 時間ステップの幅
• Δx: 空間ステップ（格子）の幅

そして、シミュレーションが安定であるためのクーラン条件は、波動方程式の場合、

μ ≤ 1

となります。つまり、c * Δt / Δx ≤ 1 でなければなりません。

3. なぜクーラン条件が重要なのか？（違反するとどうなるか）

もしこの条件を破ってしまう（μ > 1 となるような大きな Δt を選んでしまう）と、計算は「不安定」になります。

• 計算が不安定になるとは？: 計算の各ステップで生じるごく僅かな誤差（丸め誤差など）が、時間と共に雪だるま式に増幅していきます。
• 結果: 計算結果は物理的にありえない巨大な値へと発散（Inf や NaN になる）し、シミュレーションは完全に破綻します。

4. 今回のコードでの適用

今回のコードでは、この重要なルールを確実に守るために、以下のようにパラメータを設定しています。

# 安定性条件 (クーラン条件) を満たすように時間ステップを設定
CFL <- 0.5
dt <- CFL * dx / c_wave

これは、以下のことを行っています。

1. CFL <- 0.5: クーラン数 μ の目標値を 0.5 に設定しています。理論上の上限は 1 ですが、安全マージン（余裕）を持たせて 1 より小さい `0.5 にしています。
2. dt <- CFL * dx / c_wave: クーラン数の定義式 μ = c * Δt / Δx を、Δt について解き直した Δt = μ * Δx / c の形にしています。
   • dt (Δt) を、我々が設定した空間ステップ dx、波の速さ c_wave、そして安全なCFL数 0.5 から逆算して決めているのです。

このように、時間ステップ Δt を適当に決めるのではなく、空間ステップ Δx に応じてクーラン条件を満たすようにすることで、シミュレーションの安定性を保証しています。

5. まとめ

• クーラン条件: シミュレーションが安定するための、時間ステップ Δt と空間ステップ Δx の間の制約。
• 物理的な意味: シミュレーション内の波が1時間ステップで1空間ステップ以上進んではいけない。
• 数式: μ = c * Δt / Δx ≤ 1
• 重要性: この条件を守らないと、計算が発散してシミュレーションが失敗する。
• 実践: Δt は、Δx と波の速さ c から、この条件を満たすように逆算して決めるのが安全で確実な方法。

以上です。