Rで 年齢調整 を試みます。
年齢調整とは
年齢調整は、年齢構成が異なる複数の集団の間で、死亡率や罹患率などを公平に比較するための統計的な手法です。
例えば、高齢者が多いA市と、若者が多いB市があるとします。一般的に、がんや心疾患などの病気は高齢者ほど罹りやすいため、単純に「人口あたりの患者数」(粗罹患率)を比較すると、高齢者の多いA市の方が高くなる傾向があります。しかし、これは「A市の生活習慣がB市より不健康だ」からでしょうか? それとも単に「A市に高齢者が多い」からでしょうか?
この「年齢構成の違い」という要因(交絡因子といいます)を取り除き、「もし両市の年齢構成が同じだったら、どちらの罹患率が高いか」を比較するのが年齢調整です。
シナリオ設定
以下のシナリオでRコードを作成します。
- A市: 高齢化が進んだ都市
- B市: 若い世代が多い都市
- 比較するもの: ある特定の病気による年間死亡率
- 基準人口: 比較の「ものさし」として使う、全国平均などの標準的な人口構成
このシナリオでは、B市の方が本質的な死亡リスクが高いにもかかわらず、粗死亡率だけを見るとA市の方が高く見えてしまう、という状況を再現します。
Rコードによる比較
まず、必要なパッケージを読み込みます。
library(dplyr)
library(ggplot2)1. データの準備
A市、B市、そして基準人口の3つのデータセットを作成します。
-
population: 各年齢階級の人口 -
deaths: 各年齢階級の年間死亡者数
# データ作成
# A市(高齢者が多い)
city_A_data <- data.frame(
age_group = c("0-19", "20-39", "40-59", "60+"),
population = c(15000, 20000, 30000, 35000), # 合計10万人、60+が多い
deaths = c(15, 40, 150, 700) # 高齢者の死亡者数が非常に多い
)
# B市(若者が多い)
city_B_data <- data.frame(
age_group = c("0-19", "20-39", "40-59", "60+"),
population = c(30000, 40000, 20000, 10000), # 合計10万人、若年層が多い
deaths = c(36, 96, 120, 250) # 全体的に死亡率がA市より高めに設定
)
# 基準人口(比較の基準とする標準的な人口構成)
standard_pop_data <- data.frame(
age_group = c("0-19", "20-39", "40-59", "60+"),
standard_population = c(25000, 35000, 25000, 15000) # 合計10万人
)
cat("--- A市のデータ ---\n\n")
print(city_A_data)
cat("\n--- B市のデータ ---\n\n")
print(city_B_data)
cat("\n--- 基準人口のデータ ---\n\n")
print(standard_pop_data)--- A市のデータ ---
age_group population deaths
1 0-19 15000 15
2 20-39 20000 40
3 40-59 30000 150
4 60+ 35000 700
--- B市のデータ ---
age_group population deaths
1 0-19 30000 36
2 20-39 40000 96
3 40-59 20000 120
4 60+ 10000 250
--- 基準人口のデータ ---
age_group standard_population
1 0-19 25000
2 20-39 35000
3 40-59 25000
4 60+ 150002. 年齢調整なしの比較(粗死亡率)
まず、単純に「総死亡者数 ÷ 総人口」で計算される粗死亡率を比較します。
# A市の粗死亡率を計算
crude_rate_A <- sum(city_A_data$deaths) / sum(city_A_data$population)
# B市の粗死亡率を計算
crude_rate_B <- sum(city_B_data$deaths) / sum(city_B_data$population)
# 結果を表示(人口10万人あたりに換算)
cat("--- 年齢調整なし(粗死亡率)の比較 ---\n\n")
cat(sprintf("A市の粗死亡率: %.1f (人口10万人あたり)\n", crude_rate_A * 100000))
cat(sprintf("B市の粗死亡率: %.1f (人口10万人あたり)\n", crude_rate_B * 100000))--- 年齢調整なし(粗死亡率)の比較 ---
A市の粗死亡率: 905.0 (人口10万人あたり)
B市の粗死亡率: 502.0 (人口10万人あたり)実行結果の解釈: この結果を見ると、A市の粗死亡率(905.0人/10万人)は、B市の粗死亡率(502.0人/10万人)よりもはるかに高く見えます。このデータだけを見ると、「A市はB市より健康リスクが高い都市だ」と誤解してしまう可能性があります。
3. 年齢調整ありの比較(年齢調整死亡率 – 直接法)
次に、直接法という一般的な手法で年齢調整死亡率を計算します。 計算手順は以下の通りです。
- A市とB市それぞれで、年齢階級別の死亡率を計算する。
- 各市の年齢階級別死亡率を、基準人口の各年齢階級の人口に掛け合わせ、期待死亡者数を算出する。
- 算出した期待死亡者数を全年齢階級で合計する。
- 合計した期待死亡者数を、基準人口の総人口で割る。
これにより、「もしA市(B市)が基準人口と同じ年齢構成だったら、死亡率はいくつになるか」を算出できます。
# 年齢調整死亡率を計算する関数を定義
calculate_adjusted_rate <- function(city_data, standard_pop) {
# 1. 年齢階級別の死亡率を計算
city_data <- city_data %>%
mutate(age_specific_rate = deaths / population)
# 基準人口データと結合
merged_data <- left_join(city_data, standard_pop, by = "age_group")
# 2. 期待死亡者数を計算
merged_data <- merged_data %>%
mutate(expected_deaths = age_specific_rate * standard_population)
# 3. 期待死亡者数を合計
total_expected_deaths <- sum(merged_data$expected_deaths)
# 4. 基準人口の総人口で割る
total_standard_pop <- sum(standard_pop$standard_population)
adjusted_rate <- total_expected_deaths / total_standard_pop
return(adjusted_rate)
}
# A市とB市の年齢調整死亡率を計算
adjusted_rate_A <- calculate_adjusted_rate(city_A_data, standard_pop_data)
adjusted_rate_B <- calculate_adjusted_rate(city_B_data, standard_pop_data)
# 結果を表示(人口10万人あたりに換算)
cat("--- 年齢調整あり(年齢調整死亡率)の比較 ---\n\n")
cat(sprintf("A市の年齢調整死亡率: %.1f (人口10万人あたり)\n", adjusted_rate_A * 100000))
cat(sprintf("B市の年齢調整死亡率: %.1f (人口10万人あたり)\n", adjusted_rate_B * 100000))--- 年齢調整あり(年齢調整死亡率)の比較 ---
A市の年齢調整死亡率: 520.0 (人口10万人あたり)
B市の年齢調整死亡率: 639.0 (人口10万人あたり)実行結果の解釈: 年齢調整を行うと、結論が逆転しました。A市の年齢調整死亡率(520.0人/10万人)に対し、B市の年齢調整死亡率(639.0人/10万人)の方が高くなっています。
これは、B市は若者が多いという年齢構成に助けられて粗死亡率が低く見えていましたが、各年齢層における本質的な死亡リスクはA市よりも高かったことを示唆しています。
4. 結果の可視化と比較
# プロット用のデータフレームを作成
results_df <- data.frame(
city = c("A市", "B市", "A市", "B市"),
rate_type = c("粗死亡率", "粗死亡率", "年齢調整死亡率", "年齢調整死亡率"),
rate_per_100k = c(
crude_rate_A * 100000,
crude_rate_B * 100000,
adjusted_rate_A * 100000,
adjusted_rate_B * 100000
)
)
# グラフを描画
ggplot(results_df, aes(x = city, y = rate_per_100k, fill = city)) +
geom_bar(stat = "identity", width = 0.6) +
geom_text(aes(label = round(rate_per_100k, 1)), vjust = -0.5, size = 4) +
facet_wrap(~rate_type, scales = "free_y") + # 粗率と調整率でパネルを分ける
labs(
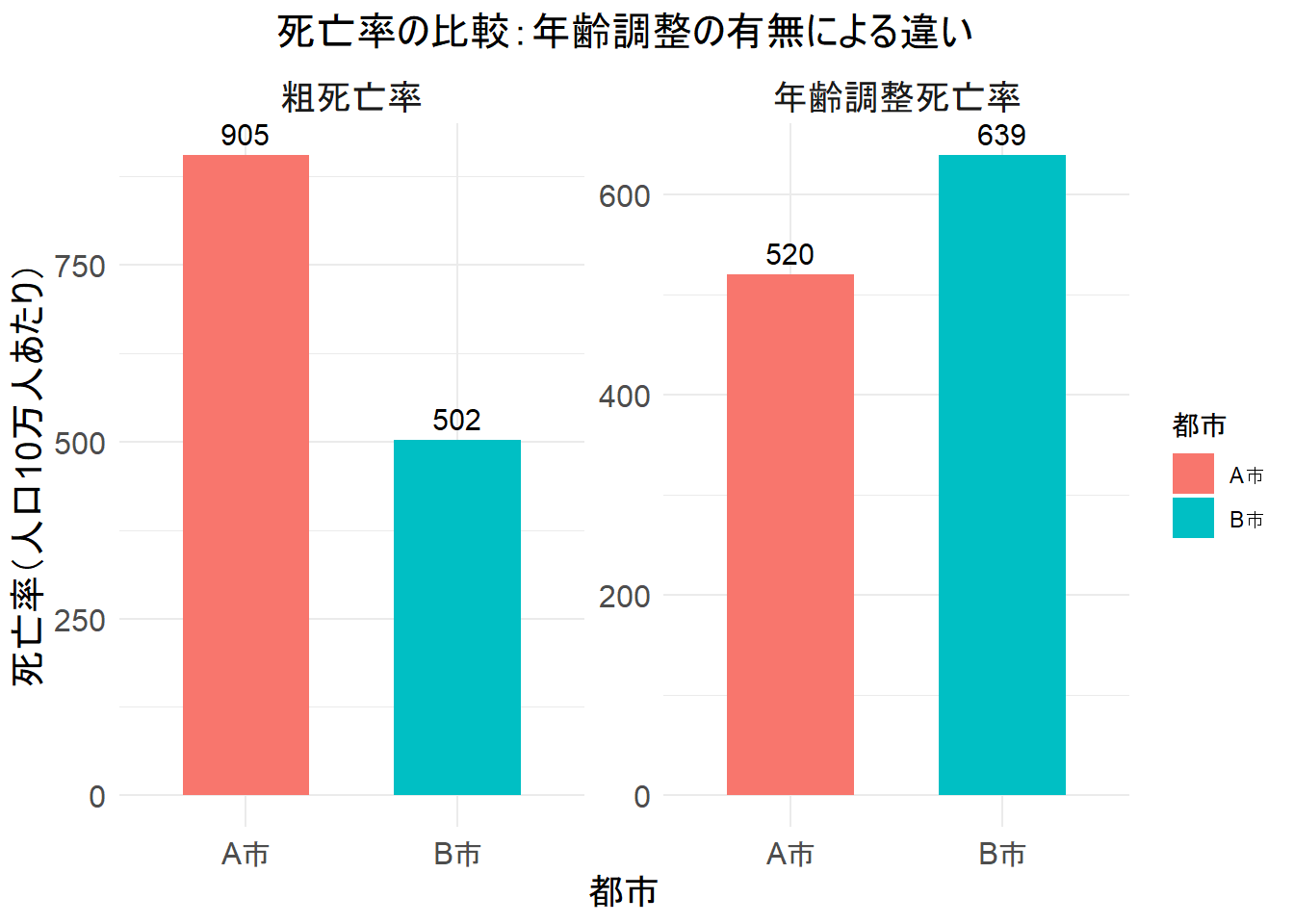
title = "死亡率の比較:年齢調整の有無による違い",
x = "都市",
y = "死亡率(人口10万人あたり)",
fill = "都市"
) +
theme_minimal() +
theme(
plot.title = element_text(hjust = 0.5, size = 16),
axis.text = element_text(size = 12),
axis.title = element_text(size = 14),
strip.text = element_text(size = 14)
)Figure 1 から、以下のことがわかります。
- 左パネル(粗死亡率): A市がB市を大幅に上回っている。
- 右パネル(年齢調整死亡率): B市がA市を上回っており、関係が逆転している。
まとめ
- 年齢調整なし(粗率): 集団の年齢構成の違いに大きく影響されるため、異なる集団間の健康水準を比較する際には誤った結論を導く可能性がある。
- 年齢調整あり(調整率): 年齢構成という要因を取り除き、より公平な「もし〜だったら」の比較を可能にする。これにより、集団の真の健康リスクを評価しやすくなる。
以上です。