Rで 確率分布:カイ2乗分布 を試みます。
本ポストはこちらの続きです。

Rで確率分布:多次元正規分布
const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...
1. カイ2乗分布とは
カイ2乗分布(Chi-squared Distribution, \(\chi^2\)分布)は、標準正規分布と密接に関連している連続確率分布です。
カイ2乗分布の定義
カイ2乗分布を理解する上で最も重要なのはその成り立ちです。 独立な確率変数 \(Z_1, Z_2, \dots, Z_k\) がそれぞれ標準正規分布 \(N(0, 1)\) に従うとします。このとき、これらの確率変数を2乗して足し合わせた和
\[X = \sum_{i=1}^{k} Z_i^2 = Z_1^2 + Z_2^2 + \dots + Z_k^2\]
が従う分布が、自由度 \(k\) のカイ2乗分布です。 この定義から、カイ2乗分布は「ズレの2乗和」や「誤差の2乗和」がどのような分布をとるかをモデル化するのに適していることがわかります。
確率密度関数 (Probability Density Function, PDF)
自由度 \(k\) のカイ2乗分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、以下の式で定義されます。
\[f(x|k) = \dfrac{1}{2^{k/2}\Gamma(k/2)} x^{k/2-1} e^{-x/2} \quad (x \ge 0)\]
この分布は、ただ一つのパラメータによってその形状が決定されます。
- \(k\): 自由度 (degrees of freedom, df)
- 分布の形状を決定する唯一のパラメータです。
- 上記の定義における「独立な標準正規分布に従う確率変数の個数」に対応します。
主な特徴
- 定義域: 2乗和から成るため、確率変数は常に非負の値 (\(x \ge 0\)) をとります。
- 形状: 自由度 \(k\) の値によって形状が大きく変化します。
- 自由度が小さいとき(特に \(k < 5\) 程度)、分布は右に大きく歪んだ(裾を引く)形状をしています。
- 自由度が大きくなるにつれて、分布の歪みは小さくなり、左右対称な形状に近づいていきます。これは、中心極限定理の帰結として、平均 \(k\)、分散 \(2k\) の正規分布に近似することが知られています。
- 代表値:
- 平均 (Mean): \(k\)
- 分散 (Variance): \(2k\)
- 最頻値 (Mode): \(k-2\) (ただし、\(k \ge 2\)の場合)
- 再生性: 自由度 \(k_1\) のカイ2乗分布と、自由度 \(k_2\) のカイ2乗分布に従う独立な確率変数の和は、自由度 \(k_1+k_2\) のカイ2乗分布に従います。
2. カイ2乗分布の応用例
カイ2乗分布は、主にカイ2乗検定と呼ばれる一連の統計的仮説検定で広く用いられます。
- 適合度の検定 (Goodness-of-fit Test)
- 観測されたデータが、理論的に想定される特定の分布(例:一様分布、正規分布など)にどの程度適合しているかを評価します。
- 例: サイコロを120回振った結果が「どの目も等しく20回ずつ出る」という理論値から有意にずれていると言えるか。
- 検定統計量 \(\chi^2 = \sum \dfrac{(\text{観測度数} - \text{期待度数})^2}{\text{期待度数}}\) が、帰無仮説のもとで近似的にカイ2乗分布に従うことを利用します。
- 独立性の検定 (Test of Independence)
- クロス集計表(分割表)で整理された2つのカテゴリカル変数が、互いに独立である(関連がない)と言えるかを検定します。
- 例: あるアンケートで「性別」と「支持政党」の間に関連性があるか。
- 適合度の検定と同様の形式の検定統計量を用います。これは社会調査や市場調査で頻繁に利用される手法です。
- 母分散の検定・信頼区間の推定
- 母集団が正規分布に従うという仮定のもとで、標本から得られた分散(標本分散)を用いて、母集団の分散(母分散)について検定したり、信頼区間を推定したりします。
3. R言語によるシミュレーション
ここでは、パラメータである自由度 \(k\) を変更した4つのカイ2乗分布を、1枚のチャートにggplot2を用いて描画します。これにより、自由度が分布の形状に与える影響を視覚的に理解します。
- ケース1:
k=1(J字型の分布) - ケース2:
k=2(指数分布と同じ形状) - ケース3:
k=5(右に歪んだ山型の分布) - ケース4:
k=20(歪みが小さくなり、正規分布に近づいた形状)
Rコード
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(0, 40, length.out = 1000)
# 2. 4つの異なる自由度を持つカイ2乗分布の確率密度を計算
# dchisq(x, df) を使用
df <- tibble(
x = x_vals
) %>%
mutate(
`自由度 k=1` = dchisq(x, df = 1),
`自由度 k=2` = dchisq(x, df = 2),
`自由度 k=5` = dchisq(x, df = 5),
`自由度 k=20` = dchisq(x, df = 20)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "parameters",
values_to = "density"
) %>%
mutate(parameters = factor(parameters, levels = c(
"自由度 k=1",
"自由度 k=2",
"自由度 k=5",
"自由度 k=20"
)))
# 4. 各パラメータに割り当てる色を名前付きベクトルで定義
manual_colors <- c(
"自由度 k=1" = "blue",
"自由度 k=2" = "red",
"自由度 k=5" = "darkgreen",
"自由度 k=20" = "purple"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = parameters)) +
geom_line(linewidth = 1.2) +
scale_color_manual(values = manual_colors) +
labs(
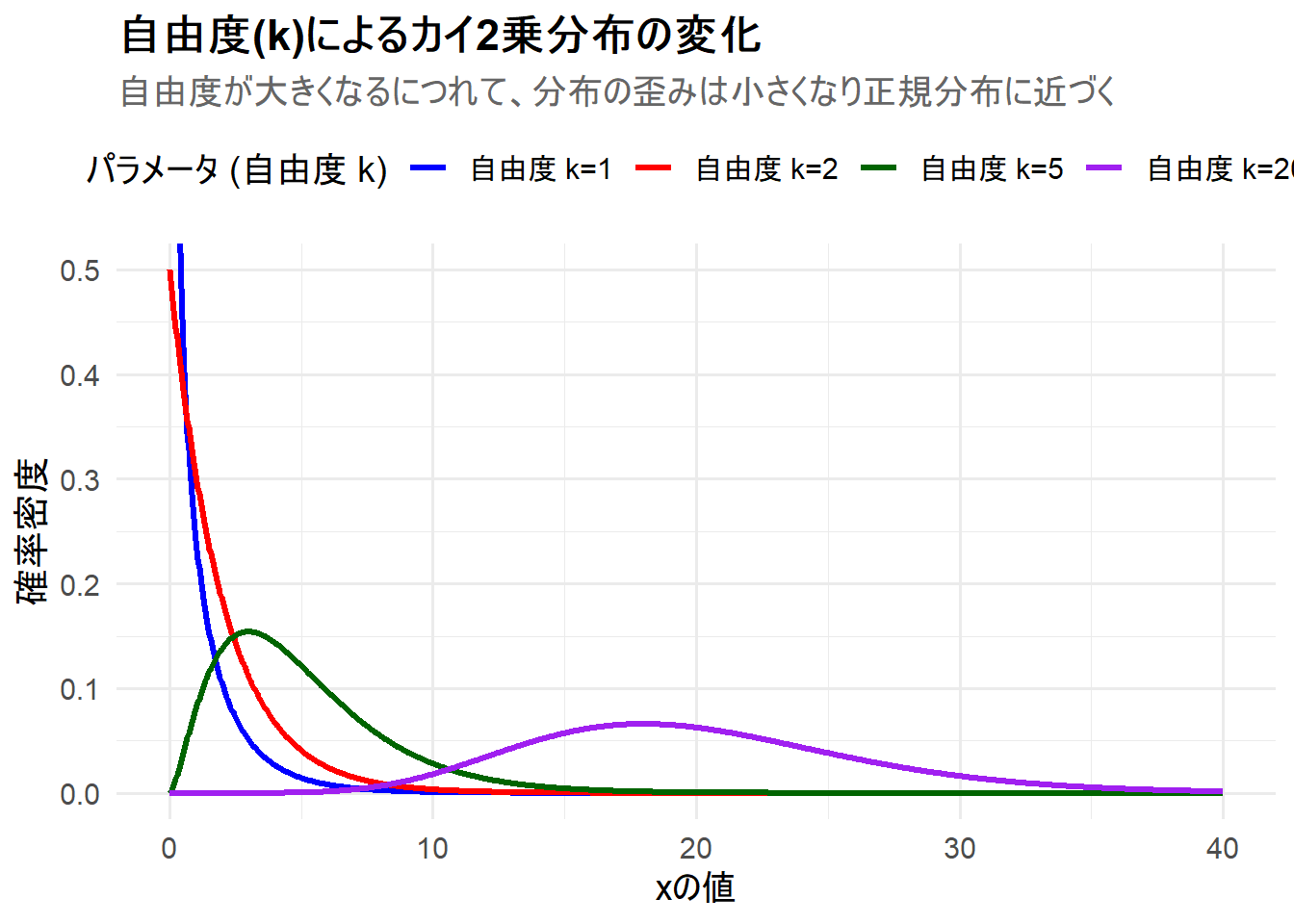
title = "自由度(k)によるカイ2乗分布の変化",
subtitle = "自由度が大きくなるにつれて、分布の歪みは小さくなり正規分布に近づく",
x = "xの値",
y = "確率密度",
color = "パラメータ (自由度 k)"
) +
# 自由度1,2の形状を分かりやすくするため、y軸の範囲を調整
coord_cartesian(ylim = c(0, 0.5)) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
)
# チャートの表示
print(p)Figure 1 の解説
上記のRコードを実行すると、4つのカイ2乗分布が描画されたチャート Figure 1 が生成されます。
-
自由度 k=1(青線): 確率密度はx=0で無限大に発散し、その後急速に減少するJ字型の分布になります。(y軸の上限を設定しているため、チャート上では発散部分は見えません) -
自由度 k=2(赤線): x=0で最大値をとり、その後単調に減少する分布となります。これは指数分布と同じ形状です。 -
自由度 k=5(緑線): はっきりとした山型の分布になりますが、ピークは左に寄っており、右側に長く裾を引く非対称な(歪んだ)形状をしています。 -
自由度 k=20(紫線): 自由度が大きくなったことで、分布の山は右に移動し(平均が20に近づく)、形状も左右の対称性が増していることがわかります。さらに自由度を大きくすると、より正規分布に近い形になります。
以上です。