Rで 確率分布:コーシー分布 を試みます。
本ポストはこちらの続きです。

Rで確率分布:ラプラス分布
const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...
1. コーシー分布とは
コーシー分布(Cauchy Distribution)は、正規分布に似た左右対称な釣鐘型の連続確率分布です。
その特徴の1つは、平均や分散といった基本的な統計量(モーメント)が定義できないことです。これは、分布の裾が重く(fat-tailed)、確率密度の減少が緩やかであるためです。
確率密度関数 (Probability Density Function, PDF)
コーシー分布に従う確率変数 \(X\) の確率密度関数 \(f(x)\) は、2つのパラメータを用いて以下のように定義されます。
\[f\left(x | x_0, \gamma\right) = \dfrac{1}{\pi\gamma \left[1 + \left(\dfrac{x-x_0}{\gamma}\right)^2\right]}\]
この分布は、2つのパラメータによってその形状が決定されます。
- \(x_0\): 位置パラメータ (location parameter)
- 分布のピークの位置を決定します。これは分布の中央値(Median)かつ最頻値(Mode)となりますが、平均(Mean)ではないことに注意が必要です。
- \(\gamma\) (ガンマ): 尺度パラメータ (scale parameter)
- 分布の広がりを決定する正のパラメータです。具体的には、ピークの高さの半分になる点の幅(半値半幅, HWHM)を表します。
主な特徴
- 形状: 位置パラメータ \(x_0\) を中心に左右対称な釣鐘型をしています。
- 平均・分散が存在しない: 裾が緩やかにしか減少しないため、平均を計算するための積分 \(\int_{-\infty}^{\infty} x f(x) dx\) が発散してしまい、値を確定できません。同様に、分散やそれ以上の高次のモーメントもすべて存在しません。
- 中心極限定理の反例: 「独立な同一分布に従う確率変数の和(または平均)は、その数が増えるほど正規分布に近づく」という中心極限定理は、平均や分散が存在しないコーシー分布には適用されません。コーシー分布に従う確率変数をいくつ足し合わせても、その和はまたコーシー分布に従うだけで、正規分布には近づきません。
- 他の分布との関係:
- 自由度1のスチューデントのt分布は、標準コーシー分布(\(x_0=0, \gamma=1\))と同一です。
- 独立な確率変数 \(Z_1, Z_2\) がともに標準正規分布 \(N(0,1)\) に従うとき、その比 \(X = Z_1/Z_2\) は標準コーシー分布に従います。
2. コーシー分布の応用例
その性質を特定の分野で利用されています。
- 物理学
- 強制共振: 外部から振動を加えたときの共振現象のエネルギー応答を記述します。
- 分光学: 原子や分子が発する光のスペクトル線の形状(輝線スペクトル)は、ローレンツ関数(コーシー分布の関数形)でモデル化されます。
- 統計学・機械学習
- ロバスト統計: 外れ値が極端に多く、または極端に大きい値をとるようなデータの分布をモデル化するために使われることがあります。
- 理論的な反例: 中心極限定理や大数の法則が成立するための「前提条件(平均・分散の存在)」の重要性を示すための、教育的な例として登場します。
3. R言語によるシミュレーション
ここでは、コーシー分布のパラメータを変更した3つのケースと、比較対象として標準正規分布およびラプラス分布を1枚のチャートに描画します。これにより、コーシー分布の形状と、他の分布と比較したときの「裾の重さ」を視覚的に理解します。
- ケース1: コーシー分布
x0=0, γ=1(標準コーシー分布) - ケース2: コーシー分布
x0=5, γ=1(位置をシフト) - ケース3: コーシー分布
x0=0, γ=2(尺度を広げる) - 比較1: 正規分布
μ=0, σ=1 - 比較2: ラプラス分布
μ=0, b=1
Rコード
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
# ラプラス分布のPDFを定義
d_laplace <- function(x, mu, b) {
1 / (2 * b) * exp(-abs(x - mu) / b)
}
# 1. 描画範囲となるx軸の値を生成
x_vals <- seq(-10, 15, length.out = 1000)
# 2. 異なるパラメータを持つ分布の確率密度を計算
# コーシー分布は dcauchy(x, location, scale) を使用
df <- tibble(
x = x_vals
) %>%
mutate(
`コーシー (x0=0, γ=1)` = dcauchy(x, location = 0, scale = 1),
`コーシー (x0=5, γ=1)` = dcauchy(x, location = 5, scale = 1),
`コーシー (x0=0, γ=2)` = dcauchy(x, location = 0, scale = 2),
`正規分布 (μ=0, σ=1)` = dnorm(x, mean = 0, sd = 1),
`ラプラス (μ=0, b=1)` = d_laplace(x, mu = 0, b = 1)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -x,
names_to = "distribution",
values_to = "density"
) %>%
# 凡例の順序を調整
mutate(distribution = factor(distribution, levels = c(
"コーシー (x0=0, γ=1)",
"コーシー (x0=5, γ=1)",
"コーシー (x0=0, γ=2)",
"正規分布 (μ=0, σ=1)",
"ラプラス (μ=0, b=1)"
)))
# 4. 各分布に割り当てる色と線種を定義
manual_colors <- c(
`コーシー (x0=0, γ=1)` = "red",
`コーシー (x0=5, γ=1)` = "orange",
`コーシー (x0=0, γ=2)` = "pink",
`正規分布 (μ=0, σ=1)` = "black",
`ラプラス (μ=0, b=1)` = "blue"
)
manual_linetypes <- c(
`コーシー (x0=0, γ=1)` = "solid",
`コーシー (x0=5, γ=1)` = "solid",
`コーシー (x0=0, γ=2)` = "solid",
`正規分布 (μ=0, σ=1)` = "dashed",
`ラプラス (μ=0, b=1)` = "dotted"
)
# 5. ggplotを使用してチャートを描画
p <- ggplot(df_long, aes(x = x, y = density, color = distribution, linetype = distribution)) +
geom_line(linewidth = 1.1) +
scale_color_manual(values = manual_colors) +
scale_linetype_manual(values = manual_linetypes) +
labs(
title = "コーシー分布と他の分布との比較",
subtitle = "正規分布やラプラス分布よりもさらに裾が重いのが特徴",
x = "xの値",
y = "確率密度",
color = "分布の種類",
linetype = "分布の種類"
) +
coord_cartesian(xlim = c(-10, 10)) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40")
) +
guides(color = guide_legend(nrow = 2))
# チャートの表示
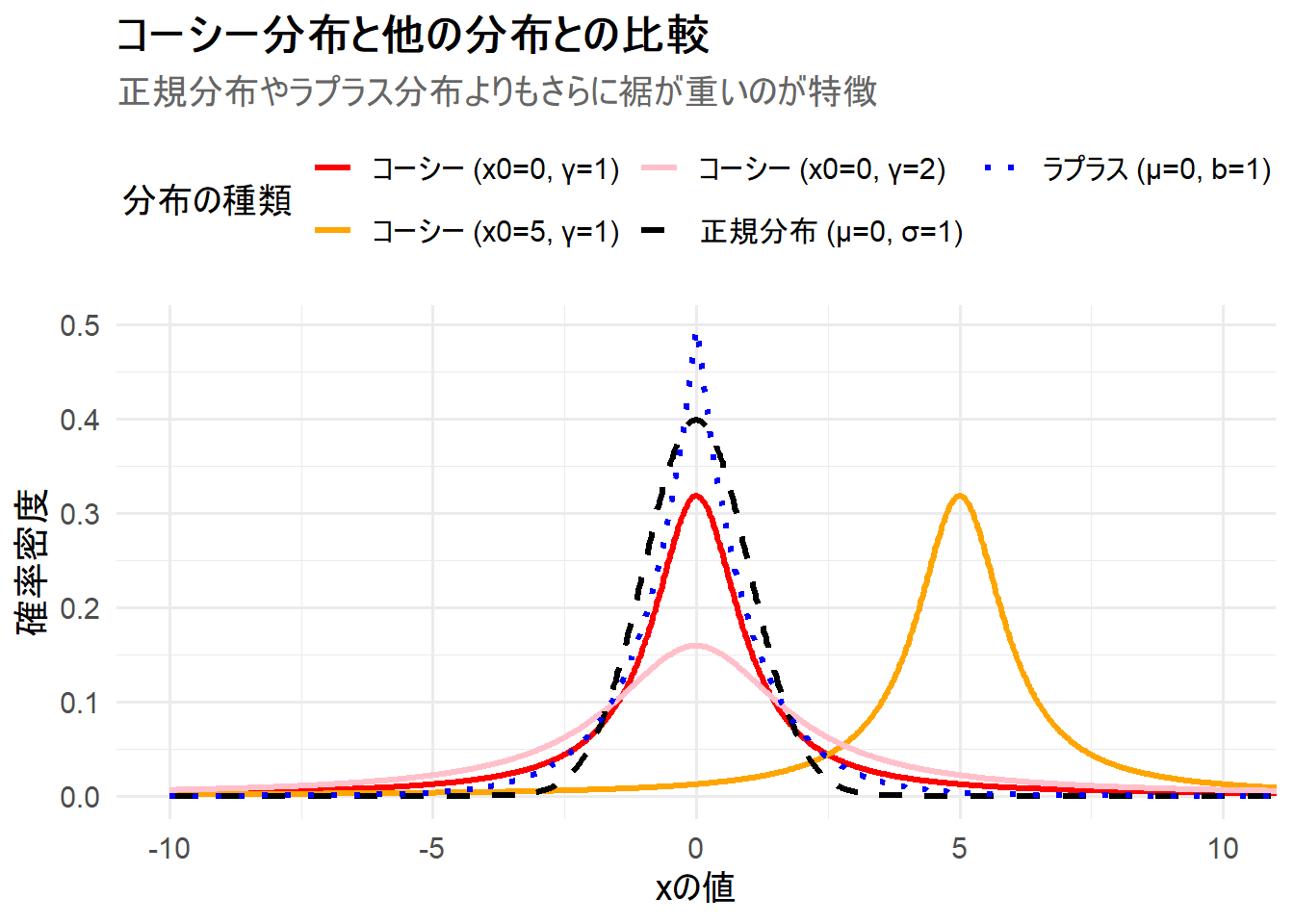
print(p)Figure 1 の解説
上記のRコードを実行すると、3つのコーシー分布と、比較のための正規分布・ラプラス分布が描画されたチャート Figure 1 が生成されます。
-
コーシー (x0=0, γ=1)(赤線): 基準となる標準コーシー分布です。中心(\(x=0\))のピークは正規分布やラプラス分布よりも低く、その分、確率が裾の方に広く分布しています。 -
コーシー (x0=5, γ=1)(オレンジ線): 位置パラメータを5にしたことで、分布がそのまま右に5だけ平行移動しています。 -
コーシー (x0=0, γ=2)(ピンク線): 尺度パラメータを2倍にしたことで、分布がより広く、平たくなっています。 -
正規分布 (μ=0, σ=1)(黒破線): 比較対象。中心でのピークが最も高いですが、\(|x|\) が大きくなると最も速く確率密度が0に近づきます。 -
ラプラス分布 (μ=0, b=1)(青点線): ラプラス分布は正規分布より裾が重いですが、Figure 1 を見ると、コーシー分布(赤線)はそのラプラス分布よりもさらに裾での確率密度が高くなっています。
このシミュレーションから、コーシー分布が他の釣鐘型分布と比較して、いかに「外れ値」が出やすい、裾の重い分布であるかが視覚的に理解できます。
以上です。