Rで 確率分布:負の二項分布 を試みます。
本ポストはこちらの続きです。

Rで確率分布:二項分布
const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...
1. 負の二項分布とは
負の二項分布(Negative Binomial Distribution)は、離散確率分布の一つです。二項分布が「試行回数を固定し、その中の成功回数」の分布をモデル化するのに対し、負の二項分布は「成功回数を固定し、その回数に達するまでの失敗回数」の分布をモデル化します。
例えば、「コインを投げて、表(成功)が10回出るまでに、裏(失敗)は何回出るか」といった状況が、負の二項分布に従います。
確率質量関数 (PMF)
成功回数が \(r\) 回になるまでに観測された失敗回数が \(k\) 回である確率 \(P(X=k)\) は、以下の式で定義されます。
\[P\left(X=k | r, p\right) = \binom{k+r-1}{k} p^r \left(1-p\right)^{k} \quad (k=0, 1, 2, \dots)\]
この式は、「合計 \(k+r\) 回の試行のうち、最後の1回は必ず成功でなければならない」という条件から導かれます。
この分布は、2つのパラメータによってその形状が決定されます。
- \(r\): 成功回数 (number of successes)
- 目標とする成功の回数です。正の整数で定義されることが多いですが、正の実数に拡張できます。
- \(p\): 成功確率 (probability of success)
- 1回の試行で「成功」と見なす結果が起こる確率です。\(0 < p \le 1\) の範囲の値をとります。
主な特徴
- 定義域: 失敗回数 \(k\) がとりうる値は、0を含む非負の整数 (\(k=0, 1, 2, \dots\)) です。
- 形状:
- 常に右に歪んだ形状をしていますが、目標とする成功回数 \(r\) が大きくなるにつれて、歪みは小さくなり、左右対称な形状に近づいていきます。
- 代表値:
- 平均 (Mean): \(E[X] = \dfrac{r(1-p)}{p}\)
- 分散 (Variance): \(V[X] = \dfrac{r(1-p)}{p^2}\)
- 分散は常に平均よりも大きくなります(\(V[X] = E[X]/p > E[X]\))。この性質を過分散(Overdispersion)と呼びます。
- 他の分布との関係:
- 幾何分布: 成功回数 \(r=1\) の負の二項分布は、幾何分布と一致します。幾何分布は「初めて成功するまでの失敗回数」の分布です。
- ポアソン分布: 負の二項分布は、ポアソン・ガンマ混合分布としても解釈できます。これにより、ポアソン分布の「平均と分散が等しい」という強い制約を緩和し、平均よりも分散が大きい「過分散」のカウントデータをモデル化するのに適しています。
2. 負の二項分布の応用例
「過分散」という性質から、ポアソン分布ではうまくモデル化できない現実世界のカウントデータ分析に利用されます。
- 生物学・生態学
- ある区画内に生息する生物の個体数。個体は完全にランダムに分布するのではなく、群れを作ったり(集中的)、縄張りを持ったり(均一的)するため、単純なポアソン分布よりも負の二項分布の方が適合することがあります。
- RNA-Seqデータ解析: 次世代シーケンサーから得られる遺伝子発現量のカウントデータは、技術的なばらつきや生物学的なばらつきにより過分散を示すため、その統計モデリングに負の二項分布が用いられます。
- 疫学
- ある地域における特定の感染症の患者数。感染症は人から人へ伝播するため、患者の発生は独立ではなく、過分散を示します。
- 事故分析
- 特定の工場や道路で発生する事故の件数。事故が起こりやすい「ホットスポット」が存在する場合、事故件数は過分散になります。
3. R言語によるシミュレーション
ここでは、目標とする成功回数 \(r\) と成功確率 \(p\) を変更した4つの負の二項分布を1枚のチャートに描画します。ロリポップチャートで表現します。
- ケース1:
r=1, p=0.5(幾何分布と同一) - ケース2:
r=5, p=0.5(成功回数を大きくする → 対称性に近づく) - ケース3:
r=5, p=0.2(成功確率を小さくする → 分布が右に広がる) - ケース4:
r=20, p=0.8(rが大きくpも大きい → ピークが左に寄り、対称性が増す)
Rコード
# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)
# 1. 描画範囲となるx軸の値(失敗回数)を生成
k_vals <- 0:40
# 2. 異なるパラメータを持つ負の二項分布の確率質量を計算
# dnbinom(k, size, prob) を使用。sizeが成功回数r, probが成功確率p
df <- tibble(
k = k_vals
) %>%
mutate(
`r=1, p=0.5` = dnbinom(k, size = 1, prob = 0.5),
`r=5, p=0.5` = dnbinom(k, size = 5, prob = 0.5),
`r=5, p=0.2` = dnbinom(k, size = 5, prob = 0.2),
`r=20, p=0.8` = dnbinom(k, size = 20, prob = 0.8)
)
# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
pivot_longer(
cols = -k,
names_to = "parameters",
values_to = "probability"
) %>%
# 確率が非常に小さいものは除外してプロットを見やすくする
filter(probability > 1e-6) %>%
# 凡例の順序を調整
mutate(parameters = factor(parameters, levels = c(
"r=1, p=0.5",
"r=5, p=0.5",
"r=5, p=0.2",
"r=20, p=0.8"
)))
# 4. 各分布に割り当てる色を定義
manual_colors <- c(
`r=1, p=0.5` = "blue",
`r=5, p=0.5` = "red",
`r=5, p=0.2` = "darkgreen",
`r=20, p=0.8` = "purple"
)
# 5. ggplotを使用してチャートを描画(ファセットで分割)
p <- ggplot(df_long, aes(x = k, y = probability, color = parameters)) +
geom_segment(aes(xend = k, yend = 0), linewidth = 0.8) +
geom_point(size = 2.5) +
facet_wrap(~parameters, ncol = 2, scales = "free") +
scale_color_manual(values = manual_colors) +
labs(
title = "パラメータ(r, p)による負の二項分布の変化",
subtitle = "過分散のカウントデータをモデル化するのに適している",
x = "失敗回数 (k)",
y = "確率"
) +
theme_minimal(base_size = 14) +
theme(
legend.position = "none",
plot.title = element_text(face = "bold"),
plot.subtitle = element_text(color = "gray40"),
strip.text = element_text(face = "bold", size = 12)
)
# チャートの表示
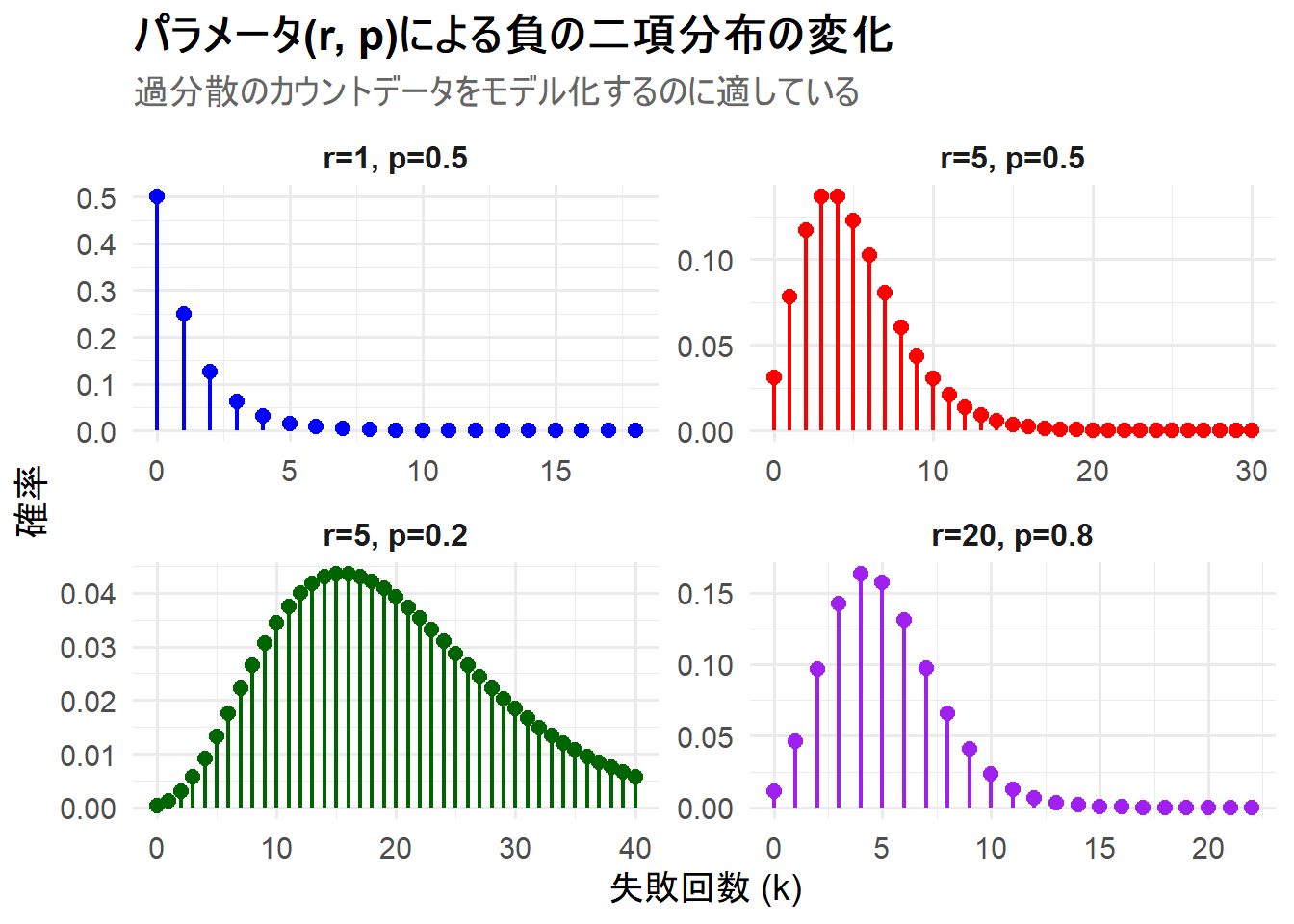
print(p)Figure 1 の解説
上記のRコードを実行すると、4つの負の二項分布が描画されたチャート Figure 1 が生成されます。
-
r=1, p=0.5(左上): 成功回数が1なので、これは幾何分布と一致します。失敗回数が0回(つまり、最初の試行で成功する)の確率が最も高くなっています。 -
r=5, p=0.5(右上): 成功回数が5に増えたことで、分布は山型になりました。平均失敗回数は \(r(1-p)/p = 5(0.5)/0.5 = 5\)回となり、そのあたりにピークがあります。 -
r=5, p=0.2(左下): 成功確率が0.2と低いため、5回成功するまでには多くの失敗が予想されます。平均失敗回数は \(5(0.8)/0.2 = 20\)回となり、分布は大きく右に広がっています。 -
r=20, p=0.8(右下): 成功回数が20と多く、成功確率も0.8と高いため、失敗はあまりしないと予想されます。平均失敗回数は \(20(0.2)/0.8 = 5\)回となり、ピークは左に寄っています。また、rが大きいため、分布の形状はより左右対称に近づいています。
以上です。