Rで確率分布:幾何分布

確率質量関数 (PMF)

成功確率 \(p\) のベルヌーイ試行において、初めて成功するまでに失敗した回数が \(k\) 回である確率 \(P(X=k)\) は、以下の式で定義されます。

\[P\left(X=k | p\right) = \left(1-p\right)^k p \quad (k=0, 1, 2, \dots)\]

この式は、「\(k\) 回連続で失敗し、その次の \(k+1\) 回目で初めて成功する」という事象の確率を表しています。

この分布は、ただ一つのパラメータによってその形状が決定されます。

• \(p\): 成功確率 (probability of success)
  • 1回の試行で「成功」と見なす結果が起こる確率です。\(0 < p \le 1\) の範囲の値をとります。

（注意：定義のバリエーション）

幾何分布にはもう一つ、「初めて成功するのは何回目の試行か」をモデル化する定義もあります。この場合、確率変数は \(Y = X+1\) となり、確率質量関数は \(P(Y=k) = (1-p)^{k-1}p\)（ただし \(k=1, 2, \dots\)）となります。Rの関数 dgeom は、ここで説明している「失敗回数」の定義に基づいています。

主な特徴

• 定義域: 失敗回数 \(k\) がとりうる値は、0を含む非負の整数 (\(k=0, 1, 2, \dots\)) です。
• 形状: \(k=0\) で最大値をとり、その後、指数的に単調減少する、右に長く裾を引く形状をしています。
• 無記憶性 (Memoryless Property): 離散分布の中では、幾何分布だけが持つ性質です。これは、「これまで \(n\) 回失敗したという事実がわかっている上で、これからさらに \(m\) 回以上失敗する確率は、最初から \(m\) 回以上失敗する確率と等しい」ということを意味します。
  • 数式で表すと、\(P(X \ge n+m | X \ge n) = P(X \ge m)\) となります。
  • 例: サイコロを振って「6」の目が出るのを待っているとします。「既に10回連続で6が出ていない」という状況でも、「次に6が出る確率」は最初と変わらず1/6です。過去の失敗は未来の確率に影響を与えません。
• 代表値:
  • 平均 (Mean): \(E[X] = \dfrac{1-p}{p}\)
  • 分散 (Variance): \(V[X] = \dfrac{1-p}{p^2}\)
• 他の分布との関係:
  • 負の二項分布: 成功回数 \(r=1\) の負の二項分布は、幾何分布と一致します。
  • 指数分布: 幾何分布は、指数分布の「離散版」と見なすことができます。両者ともに無記憶性を持ちます。

Rコード

# 必要なライブラリを読み込みます
library(ggplot2)
library(dplyr)
library(tidyr)

# 1. 描画範囲となるx軸の値（失敗回数）を生成
k_vals <- 0:20

# 2. 異なる成功確率を持つ幾何分布の確率質量を計算
# dgeom(k, prob) を使用。probが成功確率p
df <- tibble(
  k = k_vals
) %>%
  mutate(
    `p=0.1` = dgeom(k, prob = 0.1),
    `p=0.3` = dgeom(k, prob = 0.3),
    `p=0.7` = dgeom(k, prob = 0.7)
  )

# 3. ggplotで描画しやすいように、データを「ロングフォーマット」に変換
df_long <- df %>%
  pivot_longer(
    cols = -k,
    names_to = "parameters",
    values_to = "probability"
  ) %>%
  # 凡例の順序を調整
  mutate(parameters = factor(parameters, levels = c(
    "p=0.1",
    "p=0.3",
    "p=0.7"
  )))

# 4. 各分布に割り当てる色を定義
manual_colors <- c(
  `p=0.1` = "blue",
  `p=0.3` = "red",
  `p=0.7` = "darkgreen"
)

# 5. ggplotを使用してチャートを描画（ファセットで分割）
p <- ggplot(df_long, aes(x = k, y = probability, color = parameters)) +
  geom_segment(aes(xend = k, yend = 0), linewidth = 0.8) +
  geom_point(size = 2.5) +
  facet_wrap(~parameters, ncol = 1, scales = "free_y") +
  scale_color_manual(values = manual_colors) +
  labs(
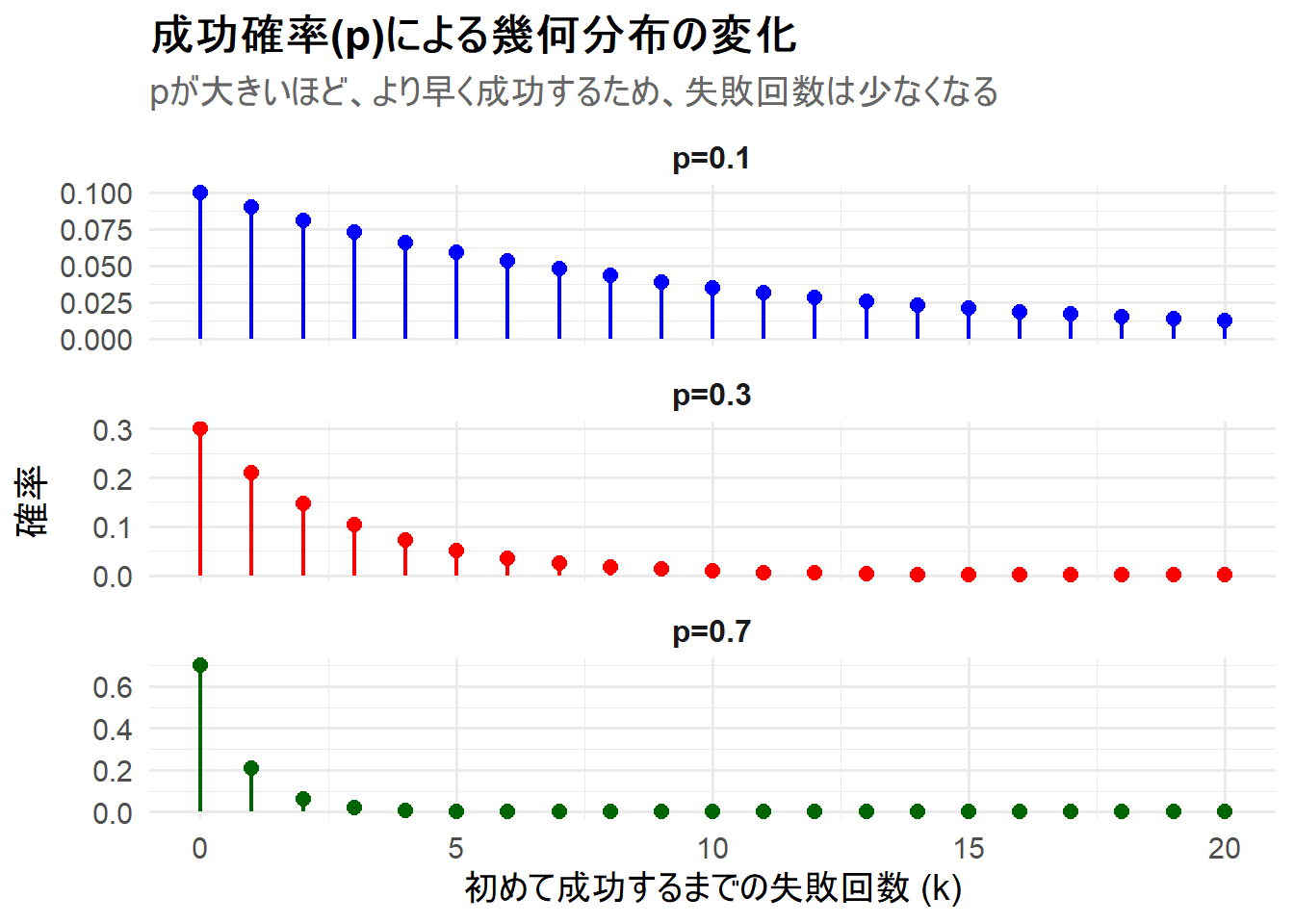
    title = "成功確率(p)による幾何分布の変化",
    subtitle = "pが大きいほど、より早く成功するため、失敗回数は少なくなる",
    x = "初めて成功するまでの失敗回数 (k)",
    y = "確率"
  ) +
  theme_minimal(base_size = 14) +
  theme(
    legend.position = "none",
    plot.title = element_text(face = "bold"),
    plot.subtitle = element_text(color = "gray40"),
    strip.text = element_text(face = "bold", size = 12)
  )

# チャートの表示
print(p)

Figure 1 の解説

上記のRコードを実行すると、3つの幾何分布が描画されたチャート Figure 1 が生成されます。

• p=0.1 (上段): 成功確率が10%と低いため、多くの失敗が予想されます。失敗回数が0回である確率（最初の試行で成功する確率）は0.1ですが、その後、確率の減少は緩やかで、多くの失敗回数にもそれなりの確率が割り当てられています。
• p=0.3 (中段): 基準となるケースです。\(p=0.1\)のケースと比べて、確率の減少が速くなっています。
• p=0.7 (下段): 成功確率が70%と高いため、ほとんど失敗しないことが予想されます。失敗回数0回の確率（最初の試行で成功する確率）が0.7と高く、その後、確率は0に近づきます。

このシミュレーションから、幾何分布の形状が成功確率 \(p\) にのみ依存し、\(p\) が大きいほど分布が左に圧縮され、より急峻な形状になることがわかります。これは、「成功しやすい試行ほど、初めて成功するまでの失敗回数は少なくなる」という直感的な理解と一致します。

以上です。